序列密碼具有實現簡單、加密速度快,、密文傳輸中的錯誤不會在明文中產生擴散等優(yōu)點,，因此應用越來越廣泛[1]。可重構技術融合了ASIC高效性和通用微處理器靈活性的實現方式,，已經廣泛應用到序列密碼算法中[2],。抽取與插入單元可重構操作解決了算法中比特級初始信息位寬不相同的操作限制，實現了算法的靈活性和高效性,，具有非常好的現實意義和創(chuàng)新性,。
    針對序列密碼算法運算操作位寬不同的特點，抽取與插入操作能夠從移位寄存器狀態(tài)中快速提取出有效狀態(tài)位來參與后續(xù)密碼運算,，解決了位寬不同的問題，從而降低了資源消耗并提高了運算速度,。例如密鑰流的生成,、復雜更新函數計算等都運用到這種操作。所以對抽取與插入單元的基本原理與實現功能的研究,，對提高序列密碼處理速度和節(jié)約序列密碼算法芯片資源具有重要的意義,。
1 序列密碼算法中抽取與插入單元操作
    序列密碼算法主要由移位寄存器、反饋函數運算單元和密鑰流函數運算單元構成,，其中反饋函數運算單元用于計算移位寄存器的更新值,，密鑰流函數運算單元用于計算最終的密鑰流。不論是反饋函數的計算還是密鑰流生成函數的運算都需要將參與運算的一個或多個移位寄存器的有效狀態(tài)位提取出來繼續(xù)完成運算,。參與運算的一個或多個移位寄存器的有效狀態(tài)位提取出來的操作稱為抽取與插入操作,。
    抽取操作過程可以用圖1（a）描述：根據預先產生的控制信息序列Ctr對受控序列In進行操作?？刂菩畔⑿蛄蠧tr中為“1”的控制位對應的受控數據依次排在Out的右側,，其余為“0”的控制位對應受控數據依次排在Out的左側，這樣能夠實現有效狀態(tài)位和無效狀態(tài)位的分離,。序列密碼算法實現過程中,，有時需要將抽取操作結果的每一位都保存下來，并且能夠在有效位運算完成后再將其插入到原始的位置上去[3],。插入操作過程可以用圖1（b）描述：當插入單元與抽取單元控制信息序列Ctr相同時,，插入單元操作能夠將抽取單元操作的有效狀態(tài)位還原,，也就是說抽取與插入單元的操作是可逆的。

    在對NESSIE工程,、ECRYPT工程[4]中的序列密碼算法分析后,，三十多種算法的運算環(huán)節(jié)包含了抽取單元操作，雖然單元操作對應的初始信息位寬相對比較復雜,，但是多數序列密碼算法操作位寬都可以歸為32 bit,、64 bit、128 bit,、256 bit四種位寬以內,。例如A5-1算法中LFSR級數為19時，運用抽取操作將參加下輪運算的第19,、18,、17、14這四個有效位比特抽取出來,，然后進行后續(xù)操作,，其余算法在這里不再贅述。表1中列出了9種序列密碼算法中密鑰流生成函數和反饋函數的運算情況,，包括變量個數和對應源操作數據的位寬,，可以得出抽取操作的源操作數位寬和目的操作數位寬。
2 抽取與插入單元的可重構硬件電路總體架構
    可重構抽取與插入單元硬件電路架構包括inverse butterfly網絡的抽取與插入基本單元電路和inverse butterfly網絡的控制信息生成電路[5],。inverse butterfly網絡的控制信息生成電路能夠同時控制inverse butterfly網絡的抽取與插入基本單元電路,。對于初始信息位寬長度為nbit的抽取與插入單元操作，基本單元電路由級inverse butterfly網絡構成,，每級網絡需要n/2 bit控制信息,，一共需要nlogn/2 bit的控制信息并且由nbit的初始信息通過控制信息生成電路生成。
    例如初始信息位寬為256 bit的抽取與插入單元操作中,，對應的單元基本電路由8級inverse butterfly網絡構成,，共需要1 024 bit控制信息。當兩個單元初始控制信息相同時,，控制信息生成電路生成的控制信息有以下關系：抽取基本單元電路的第1級控制信息與插入基本單元電路的第8級控制信息相同,，需要將抽取單元的各級電路生成信息還原為各自對應輸入信息時，能夠利用插入單元的特點：在控制信息相同的情況下,，可以將抽取單元各級的生成信息作為插入單元的輸入信息來實現,。由此得到抽取與插入單元電路的實現是一個可逆的過程。

3 可重構控制信息生成電路
3.1 控制信息的生成算法
    通過對benes,、butterfl,、inverse butterfly、banyan以及clos等多種網絡結構的分析和研究得知,，抽取與插入單元運用了inverse butterfly網絡控制信息生成算法[6],。nbit初始信息對應的inverse butterfly網絡需要nlogn/2 bit控制信息,，這些信息均由nbit初始信息譯碼生成，控制信息算法[6]如下：
    (1)計算初始控制信息抽頭
    PPC[0]=control[0]
    For i=1,，2,，……，n-2
        PPC[i]=PPC[i-1]+control[i]
    (2)計算inverse butterfly網絡控制信息生成算法
    sel={}
    For i=1,，2,，……，lg(n)
        k=2i-1
        For j=0,，1,，……，n/2i-1
            temp=LROTC(0K,，PPC[j?鄢2i+k-1])
            sel[i]=temp||sel[i]
    其中：
    ①LROTC(a, rot)表示左循環(huán)取反填充,，a是輸入，rot是左循環(huán)次數,。
    ②0k代表長度為k的“0”比特串,。
    ③PPC[a]代表從原始控制信息的第0抽頭到第a抽頭的1的個數。
    ④i表示inverse butterfly網絡的第i級,。
    ⑤k表示第i級中每個子單元需要的控制信息位數,，也表示每個子單元中處在右側部分的輸入位數。
3.2 控制信息生成連加電路算法設計
    針對控制信息生成電路位寬多變的特點,，連加比特電路有多種實現模式,。在處理連加電路時，提出了相鄰比特兩兩相加以減少電路寄存器數目的操作,，大幅度減小了電路設計面積并且提高了電路運行效率。以8 bit十進制連加電路為例,，(其中a0～7表示8 bit連加電路初始信息位寬,，b1～4表示連加電路相鄰2 bit相加信息位寬，U1～8表示連加電路結果信息位寬)如圖2所示,。

    根據電路圖所示有以下關系公式：
       
    通過（1）,、（2）兩個公式可以極大地節(jié)省連加電路的運算時間，而且降低了寄存器對功耗的影響,。提高了整體運算電路的運算速度,。
4 基于inverse butterfly網絡的可重構抽取與插入操作基本單元
    抽取與插入單元是序列密碼算法實現高效性和靈活性的核心模塊?；趇nverse butterfly網絡提出了抽取與插入操作基本單元,，且nbit的操作數位寬對應inverse butterfly網絡共有l(wèi)ogn級，抽取操作基本單元的特點是級數由上到下逐級增大,，并且在第i級中,，共有n/2i個子單元,，每個子單元輸入數據位寬為2i bit。對于每級中的子單元,，左右單元各占一半的輸入,，左右部分的位寬均為2i-1 bit，而且每個子單元都需要2i-1 bit的控制信息,。
    圖3所示抽取操作基本單元位寬為16 bit的4級inverse butterfly網絡[7],，第一級有8個子單元，每個子單元對應2 bit數據輸入和1 bit控制信息,；第二級有4個單元,，每個子單元對應4 bit數據輸入和2 bit控制信息；第三級有2個單元,，每個子單元對應8 bit數據輸入和4 bit控制信息,；第四級有1個單元，單元對應16 bit數據輸入和8 bit控制信息,。

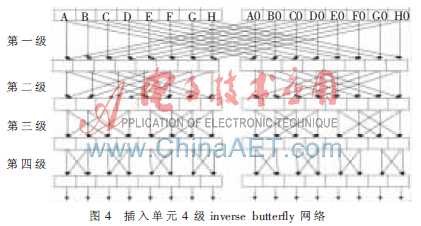
    插入單元的nbit操作數位寬對應的inverse butterfly網絡和抽取單元同樣有l(wèi)ogn級,。綜上所述，當兩個單元控制信息相同時,，抽取與插入基本單元的實現過程是可逆的,，插入操作運算能夠將抽取操作運算結果還原為初始數據信息。圖4為插入基本單元位寬為16 bit的4級inverse butterfly網絡,，可知第一級有1個子單元,，子單元對應16 bit數據輸入和8 bit控制信息；第二級有2個單元,，每個子單元對應8 bit數據輸入和4 bit控制信息,；第三級有4個單元，每個子單元對應4 bit數據輸入和2 bit控制信息,；第四級有8個子單元,，每個子單元對應2 bit數據輸入和1 bit控制信息。由此可以得到位寬為256 bit的8級inverse butterfly網絡,，在此不再贅述,。

5 性能分析
    本文提出的設計采用Verilog語言描述，在Quartus9.0環(huán)境下編譯,，選用Altera StratixIII系列器件的EP3SL340F1760C4為目標器件進行了綜合,，表2給出抽取和插入單元加載到FPGA中的時鐘頻率和資源占用情況。另外本設計使用NC-Verilog對批量數據進行了仿真測試,，驗證結果均正確,。基于CMOS 0.13 μm工藝庫，在Synopsys公司的Design Compiler上進行了邏輯綜合,、優(yōu)化,。結果如表3所示。

    綜上所述,，本文基于抽取和插入單元的基本原理,，提出并實現了可重構硬件電路，在保證單元運算靈活性
和準確性的同時,，有效降低了功耗,，并且滿足了不同位寬序列密碼的操作要求。通過在FPGA上驗證,，抽取與插入單元的設計結果正確,、高效。能夠滿足多種對稱密碼算法的實現需求,，同時為可重構密碼芯片的設計和運用奠定了良好的基礎,。
參考文獻
[1] Luo Qibin，Zhang Jian,，Status Quo.Development of stream cipher.Information And Electronic Engineering,，2007，1(2).
[2] ADAM J E.Reconfigurable computing for Symmetric-Key[D]. 2002.
[3] Shi Zhijie,，Ruby B L.Subword sorting with versatile permuta-tion instructions.Proceedings of the International Conference on Com-puter Design(ICCD 2002),，2002(9)：234-241.
[4] Liu Yunyi，Qin Tuanfa,，Ni Wansun,，et al.The brief evaluations of the candidates to the ECRYPT stream ciphers. Information Securityand Communication Secrecy，2006,，7.
[5] LEE R B,，RIVEST R.L，ROBSHAW M.J.B,，et al.On permutation operations in cipher design.Proceedings of the International Conference on Information Technology (ITCC),，2004，2(4)：569-577.
[6] SHI Z J,，Ruby B.L.Implementation complexity of bit permutation instructions department of electrical engineering. Princeton University,，Princeton,，NJ 08544 USA,，2003.
[7] YANG X，VACHHARAJANI M,，LEE R B.Fast subword  permutation instructions based on butterfly networks,，Proceedings of Media Processors 2000(SPIE 2000)，2000(1)：80-86.