摘 要：設(shè)計(jì)了一種新的能量獎勵機(jī)制，以提高微正則退火算法擺脫局部極值點(diǎn)的能力。在狀態(tài)轉(zhuǎn)移被拒絕后,，通過比較兩個(gè)能量參數(shù)的大小來啟動獎勵操作。獎勵方式依舊為幾何增長方式,，但增長幅度改為一定區(qū)間內(nèi)的線性調(diào)節(jié)。給出了一個(gè)采用改進(jìn)算法的經(jīng)典的單配送中心實(shí)例,，它提高了微正則退火基本算法的優(yōu)化效果,，降低了搜索過程停滯在局部極值的概率，它搜索到的運(yùn)輸費(fèi)用更貼近最佳解,。
關(guān)鍵詞：車輛路徑問題,；微正則退火算法；組合優(yōu)化
?
配送車輛路徑問題VRP（Vehicle Routing Problem）是指向一批客戶配送物資,，客戶的位置和貨物需求量已知,，現(xiàn)有若干可供派送的車輛，車輛的運(yùn)載能力給定,，每輛車都從起點(diǎn)出發(fā),，完成若干客戶點(diǎn)的運(yùn)送任務(wù)后再回到起點(diǎn)，現(xiàn)尋求以最少的車輛數(shù),、最小的車輛總行程來完成貨物配送任務(wù),。
車輛路徑問題是物流配送中的關(guān)鍵決策問題，已有研究表明該問題屬于NP難題[1-2],。求解該問題有兩類方法,，一類是精確算法，另一類是啟發(fā)式算法[3-5],，后者力圖在有限的時(shí)間內(nèi)找到大規(guī)模問題的滿意解,，得到不少工程人員的關(guān)注。本文研究的微正則退火算法MA（Micro-canonical Annealing）也屬于啟發(fā)式算法的范疇,，有關(guān)研究表明,，該算法具有實(shí)施簡單、運(yùn)行速度快,、優(yōu)化效果出色等優(yōu)點(diǎn)[6],。筆者曾提出一種對該算法的改進(jìn)思路，針對算法迭代后期的優(yōu)化進(jìn)程放緩問題，適時(shí)給予能量獎勵策略,，提高了在旅行推銷員問題上的搜索性能,。本文改進(jìn)了這種能量獎勵思想，將其用于配送路徑的優(yōu)化問題,。實(shí)驗(yàn)研究發(fā)現(xiàn),，改進(jìn)算法提高了最終解的質(zhì)量，能夠得到更低的運(yùn)輸費(fèi)用,。
1 配送車輛路徑問題的數(shù)學(xué)模型
根據(jù)約束條件和目標(biāo)函數(shù)的差異,，車輛路徑問題的數(shù)學(xué)模型可寫成多種形式,。最簡單的情形是設(shè)計(jì)從一個(gè)位置出發(fā),，到多個(gè)不同位置的客戶點(diǎn)的最優(yōu)配送路徑，即尋找一個(gè)運(yùn)費(fèi)最小的路徑集合,，并滿足如下條件：
首先,，每條配送路徑上各個(gè)客戶的需求量之和不超過汽車載貨量。
其次,，每個(gè)客戶的需求必須滿足,，且只能由一輛汽車送貨。
先作如下定義：i,、j 為任意兩個(gè)客戶的標(biāo)號,，i、j∈N,；N = { 1, 2,…, n},，n為客戶的數(shù)目，標(biāo)號0表示配送中心（即假定只有一個(gè)配送中心的情形）,；k為配送車輛的標(biāo)號,；k∈k，k = {1, 2 , …, m},，m為車輛的數(shù)目,；Ci,j為客戶i、j 之間的距離,；Xijk為路徑?jīng)Q策變量,，當(dāng)?shù)趉輛車從客戶i駛向客戶j時(shí)Xijk為1，否則Xijk為0,；Yik為車輛與客戶的配對參數(shù),，當(dāng)車輛k服務(wù)客戶i時(shí)取值為1，否則取0,；wj為客戶j的貨物需求量,；D為車輛的最大載貨量，Cmin為最少總費(fèi)用,?？山⑷缦履Ｐ停?BR> 
式（1）為目標(biāo)函數(shù),，使得總費(fèi)用最小,；式（2）表示每個(gè)客戶都被訪問且僅被訪問一次,；式（3）、（4）為每條巡回路徑上的配送限制,；式（5）為車輛的載貨量限制,。
2? 微正則退火算法及改進(jìn)策略
2.1 算法的基本原理
微正則退火與傳統(tǒng)模擬退火的差異在于，它不再直接依賴系統(tǒng)溫度,，配分函數(shù)Z的形式為：
式（6）中,，E0是初始能量值，K(P)是動量P在狀態(tài)C下的能量,，上式中沒有出現(xiàn)溫度參數(shù),。
在這一仿真方法中，假設(shè)熱系統(tǒng)中存在一個(gè)具有能量交換能力的妖,，它的作用類似式（6）中的動量P,。這只妖可以在狀態(tài)空間中隨機(jī)行走，并通過改變熱系統(tǒng)的狀態(tài)變量達(dá)到調(diào)節(jié)系統(tǒng)能量的目的,。仿真過程中,，系統(tǒng)與妖的能量之和保持定值并且逐步降低，促使系統(tǒng)積累足夠的能量以脫離亞穩(wěn)態(tài),。令妖的能量為ED,，ED為正數(shù)且初始值一般等于0。此時(shí)Z的形式為：
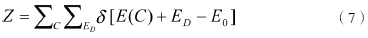
系統(tǒng)初始狀態(tài)可以隨機(jī)配置,，妖在狀態(tài)空間中每隨機(jī)行走一步,，就會嘗試改變當(dāng)前的系統(tǒng)狀態(tài)，若此舉能降低系統(tǒng)能量,，則系統(tǒng)接收狀態(tài)變遷,。與此同時(shí)，系統(tǒng)釋放的能量將會被妖吸收,。當(dāng)這種退火機(jī)制用于尋求目標(biāo)函數(shù)最小值時(shí),，狀態(tài)空間對應(yīng)于自變量空間，系統(tǒng)能量對應(yīng)于目標(biāo)函數(shù)值,。妖的能量變更可用如下公式表達(dá)：
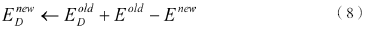
式中Enew,、Eold分別表示新舊狀態(tài)所對應(yīng)的系統(tǒng)能量。為保證妖的能量總是正值,，若妖的隨機(jī)行走導(dǎo)致系統(tǒng)能量升高且升高幅度超過ED,，該狀態(tài)轉(zhuǎn)移將被拒絕。另一方面，妖的能量ED也有上界約束M,，該值隨著迭代過程逐步減小,。
2.2 能量獎勵策略
妖的當(dāng)前能量ED直接限制了系統(tǒng)能量回升的最大幅度，這一數(shù)值刻畫出系統(tǒng)脫離亞穩(wěn)態(tài)的能力大小,。在算法后期,，由于Emax的作用，ED總體處于下降趨勢,，劣狀態(tài)被接受的概率非常低,，若系統(tǒng)陷入一個(gè)比較深的能量局部極小狀態(tài)，確定性的狀態(tài)接受規(guī)則將使得系統(tǒng)幾乎不能脫離該狀態(tài),。
筆者曾考慮對妖的能量ED施加一種幾何方式的能量獎勵策略,，在拒絕新狀態(tài)后，適當(dāng)增大ED的數(shù)值,，以期逐步提高妖脫離局部極值的能力,。具體操作方法是：對ED實(shí)施比例為q的增幅,，即ED←ED×(1＋q),，其中q值一般很小。在先前所做的實(shí)例仿真中發(fā)現(xiàn),，一種被稱為無上界約束的能量獎勵策略效果很小,，這種方式在實(shí)施能量獎勵后不檢查ED是否超過Emax（當(dāng)妖主動吸收能量后仍然要對ED做越界約束）。
3?改進(jìn)微正則退火算法的實(shí)施
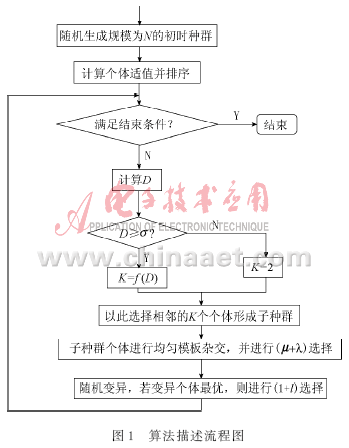
微正則退火算法用于組合優(yōu)化時(shí),，算法的實(shí)施流程與傳統(tǒng)模擬退火算法類似,，具體體現(xiàn)在：第一，算法需要一個(gè)初始解,，算法的主過程將在該初始解上執(zhí)行領(lǐng)域變換,；第二，算法的主流程也是雙層循環(huán)結(jié)構(gòu),，內(nèi)循環(huán)按照退火策略更新狀態(tài),。外循環(huán)是縮減妖的能量上界約束M（模擬退火中是降低溫度）。
3.1 鄰域變換
領(lǐng)域解的產(chǎn)生有兩類常用方法,，第一類是路徑間優(yōu)化,，如路徑插入法和路徑交換法。第二類是路徑內(nèi)優(yōu)化,，如常用的二交換法,，假設(shè)( i，i + 1) 和( j,，j + 1) 是當(dāng)前路徑的兩條邊, 二交換后得到兩條新邊( i,，j) 和(i+1，j +1)，且原路徑中j和i+1節(jié)點(diǎn)之間的整段路徑需要翻轉(zhuǎn),，后續(xù)實(shí)驗(yàn)中使用了二交換方法,。
3.2 退火策略
妖的能量上界約束M值在內(nèi)循環(huán)中保持不變，內(nèi)循環(huán)結(jié)束后該值將按比例縮減,，即有M(i+1) =αM(i),，M(i)表示內(nèi)循環(huán)執(zhí)行了i次后的M值，α為縮減系數(shù),。
??? 內(nèi)循環(huán)的停止標(biāo)準(zhǔn)包括兩種情形,，一是在當(dāng)前M下，已經(jīng)嘗試了U次循環(huán),；二是在當(dāng)前M下,，最好解成功已改進(jìn)了L次，其中U與L是預(yù)定義的常數(shù),。
外循環(huán)在M低于預(yù)設(shè)值e,，或找到指定解時(shí)即被終止，最后輸出最終搜索結(jié)果,。
3.3 改進(jìn)的能量獎勵策略
實(shí)施能量獎勵策略時(shí),，需要做好兩項(xiàng)決策，首先是獎勵時(shí)機(jī)的選擇,，之前筆者曾設(shè)計(jì)過一種容忍機(jī)制,，只在當(dāng)前狀態(tài)沒改變累計(jì)達(dá)到一定次數(shù)后才實(shí)施獎勵，這種方式操作起來比較簡單,，但容忍次數(shù)的設(shè)置沒有可靠依據(jù),，只能通過經(jīng)驗(yàn)預(yù)定。本文實(shí)驗(yàn)中通過能量差額比較的方法來啟動能量獎勵步驟,，當(dāng)未被接受的能量差額累計(jì)值超過某個(gè)數(shù)額時(shí),，妖將獲得一次能量獎勵。
為此,，需再設(shè)定一個(gè)變量Er和Eg,。Er以累加的方式記錄連續(xù)的、未被接收的能量差額值,。譬如當(dāng)前領(lǐng)域變換得到的新狀態(tài)將使得系統(tǒng)能量值提高12,，而妖的能量值ED=8，按照狀態(tài)接收規(guī)則,，新狀態(tài)不被接受,，此時(shí)Er的數(shù)值將增加12。若新狀態(tài)被接收,，此時(shí)Er將被清零,，使得能量獎勵機(jī)制只在當(dāng)前解連續(xù)多次沒有改進(jìn)時(shí)發(fā)揮作用,。若新狀態(tài)使得系統(tǒng)能量回升過大，Er的累計(jì)操作將會被忽略,，實(shí)際執(zhí)行時(shí),，若未被接受的能量回升值超過了妖的最大能量上限M，該差額不被計(jì)入Er,。
Eg控制了獎勵操作的閾值,，可直接令Eg＝M，并隨M的縮減而變化,。在算法運(yùn)行過程中,，當(dāng)Er>Eg時(shí)，將執(zhí)行能量獎勵操作,，隨后Er被清零,。
能量獎勵策略的另一項(xiàng)決策是確定獎勵幅度，在最初的算法改進(jìn)方案中,，執(zhí)行固定比例的獎勵（如獎勵增幅q可設(shè)為0.01）,。考慮到妖在算法運(yùn)行前期獲得額外獎勵的需求并不強(qiáng)烈,，而陷入停滯狀態(tài),，往往是算法后期才表現(xiàn)出來，因此本文設(shè)計(jì)了一種新的獎勵方法,，增幅q將以線性增大的方式在預(yù)先選定的區(qū)間內(nèi)變化（如0.005～0.05）,。
3.4 算法流程
（1）相關(guān)變量初始化操作,，創(chuàng)建初始可行解，并釋放能量ED＝0的妖,。
?。?）外層循環(huán)控制，若M小于e則終止程序,。
?。?）更新M，按比例縮減,；更新Eg與q,。
（4）內(nèi)循環(huán)控制,，若滿足3.2節(jié)所列條件,，程序返回到步驟（2）。
?。?）創(chuàng)建鄰域解,。
?。?）若系統(tǒng)能量值降低或系統(tǒng)能量值增大幅度小于ED時(shí)均接受鄰域解；更新Er,；更新ED,。
（7）若領(lǐng)域狀態(tài)被拒絕,，則將此未被接收的能量增幅記入Er中,，并比較Er與Eg，以決定是否實(shí)施能量獎勵,。
?。?）返回步驟（4）。
4 實(shí)例分析
采用包含20個(gè)需求點(diǎn)的單配送中心實(shí)例來驗(yàn)證改進(jìn)算法的效果[4],。其中運(yùn)輸車輛的最大載貨量D等于8,。根據(jù)有關(guān)文獻(xiàn)的建議，已有經(jīng)驗(yàn)公式估計(jì)車輛總數(shù)[7],，本文約定有6輛運(yùn)輸車,。配送中心的坐標(biāo)為（52，4）,，其他客戶節(jié)點(diǎn)的坐標(biāo)及需求量如表1所示,。
?
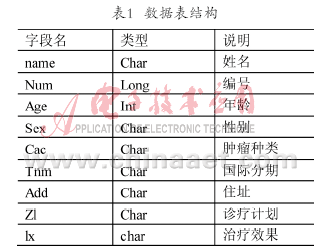
根據(jù)筆者之前對該實(shí)例的模擬經(jīng)驗(yàn)，令初始M=100,；α=0.95,；U=100；L=30,；e=0.01,；q在0.005～0.05之間變化。在上述參數(shù)下,，微正則退火基本算法的表現(xiàn)比較穩(wěn)定,。
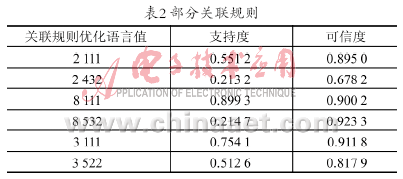
表2展示了改進(jìn)算法中能量獎勵策略的效果。其中算法1指未進(jìn)行任何改進(jìn)的微正則退火基本算法,；算法2施加了簡單的能量獎勵策略（即2.2節(jié)描述的方式）,；算法3以能量差額比較的方式啟動獎勵策略，獎勵幅度固定,；算法4指以能量差額比較的方式啟動獎勵策略,，獎勵幅度線性變化。各組算法均以相同的初始解開始搜索,，并對30次隨機(jī)實(shí)驗(yàn)的結(jié)果進(jìn)行統(tǒng)計(jì),。
?
?
為了便于比較，以運(yùn)輸費(fèi)用降到901作為算法搜索成功的標(biāo)準(zhǔn),，此運(yùn)輸費(fèi)用是本實(shí)例一個(gè)較好的結(jié)果,。表2中的第二列指最終找到這個(gè)滿意解的次數(shù),。第三列指該算法的全部30次實(shí)驗(yàn)中，最終運(yùn)輸費(fèi)用距離901的平均距離（費(fèi)用差額值占901%）,，該比例越小,，說明最終解越好。
對表2分析可見：首先,，能量獎勵策略是有效的,，從一定程度上提高了算法搜索到指定滿意解的能力。實(shí)施了能量獎勵策略的三組算法,，對于本實(shí)例的搜索成功次數(shù)都比基本算法要高,。其次，利用能量差額比較來判定是否獎勵的效果得到了驗(yàn)證,，與簡單的能量獎勵策略相比,，它的成功次數(shù)更大。再次,，從表2的第三列可知,，實(shí)施能量獎勵策略后，多次實(shí)驗(yàn)的平均解要更列可知,，實(shí)施能量獎勵策略后,，多次實(shí)驗(yàn)的平均解要更接近指定的滿意解，而且本文提出的能量獎勵實(shí)施策略進(jìn)一步提高了微正則退火算法的搜索能力,。
圖1是上述實(shí)驗(yàn)中4種算法最低運(yùn)輸成本的變化軌跡,。可以看出微正則退火基本算法在最開始階段的下降速度很快,，但到后期不如其他算法,。根據(jù)能量獎勵策略的特點(diǎn)可知，它使得整個(gè)搜索過程更為平緩一些,，前期目標(biāo)函數(shù)值下降稍慢,，這從一定程度上消弱了微正則退火算法本身的快速優(yōu)化優(yōu)勢，但從圖1可發(fā)現(xiàn),，施加了改進(jìn)的能量獎勵策略后，對上述問題有了明顯的改善,。
?
?
微正則退火算法具有快速收斂特征,，不少研究文獻(xiàn)中都探討了這種退火算法的工程應(yīng)用價(jià)值。本文首先對筆者曾提出的能量獎勵策略進(jìn)行改進(jìn),，根據(jù)能量差額比較的方法來決定是否啟動獎勵操作,，并且嘗試能量增幅比例q按線性方式調(diào)節(jié)。隨后將新的改進(jìn)算法應(yīng)用車輛路徑優(yōu)化問題,，并通過一個(gè)典型的單配送中心實(shí)例給出了初步比較,。實(shí)驗(yàn)結(jié)果證明這種改進(jìn)的微正則退火算法用于路徑優(yōu)化是十分有效的,。本文的改進(jìn)思路也有缺點(diǎn)，增加了算法代碼的復(fù)雜程度,，理論上會耗費(fèi)更長的搜索時(shí)間,，但在本實(shí)例上表現(xiàn)不明顯，應(yīng)該用更大規(guī)模的實(shí)例來檢驗(yàn),，這將是下一步的工作內(nèi)容,。
參考文獻(xiàn)
[1] PAOLO T, DANIELE V. The vehicle routing problem[M]. Philadelphia: Society for Industrial and Applied Mathematics,2002.
[2]?祝崇雋, 劉民, 吳澄. 供應(yīng)鏈中車輛路徑問題的研究進(jìn)展及前景[J]. 計(jì)算機(jī)集成制造系統(tǒng), 2001, 7 (11) :1-6.
[3]?崔雪麗, 馬良, 范炳全. 車輛路徑問題( VRP) 的螞蟻搜索算法[J]. 系統(tǒng)工程學(xué)報(bào), 2004, 19(4) :418-422.
[4]?胡大偉, 朱志強(qiáng), 胡勇. 車輛路徑問題的模擬退火算法[J]. 中國公路學(xué)報(bào), 2006, 19(4) :123-126.
[5]?張波, 葉家瑋, 胡郁蔥. 模擬退火算法在路徑優(yōu)化問題中的應(yīng)用[J]. 中國公路學(xué)報(bào), 2004,17(1):79-81.
[6]?CREYTZ M. Microcanonical Monte Carlo simulation[J]. Physical Review Letters, 1983, 50(19): 1411-1414.
[7]?李軍, 謝秉磊, 郭耀煌. 非滿載車輛調(diào)度問題的遺傳算法[J]. 系統(tǒng)工程理論與實(shí)踐, 2000, 20(3):235-239.