??? 摘 要:在心電信號(hào)采集過(guò)程中,混雜著各種各樣的干擾信號(hào)。利用心電信號(hào)及各種干擾信號(hào)之間相互統(tǒng)計(jì)獨(dú)立的關(guān)系,采用獨(dú)立分量分析對(duì)心電信號(hào)進(jìn)行處理。實(shí)驗(yàn)結(jié)果表明,獨(dú)立分量分析方法不但將工頻干擾等干擾信號(hào)成功地分離出來(lái),而且較好地保留了原始心電信號(hào)中的細(xì)節(jié)信息。
??? 關(guān)鍵詞:心電信號(hào)(ECG);獨(dú)立分量分析;信號(hào)處理
?
??? 獨(dú)立分量分析ICA(Independent Component Analysis)是近來(lái)發(fā)展起來(lái)的一種新的盲源分離方法BSS(Blind Source Separation)[1]。ICA處理的對(duì)象是一組相互統(tǒng)計(jì)獨(dú)立的信源經(jīng)線性組合而產(chǎn)生的混合信號(hào),其最終目的是在源信號(hào)和混合方式都未知的情況下,從混合信號(hào)中恢復(fù)出源信號(hào)各個(gè)獨(dú)立成分的過(guò)程。ICA這種能夠提取獨(dú)立成份的特性已被廣泛應(yīng)用于生物醫(yī)學(xué)信號(hào)處理、混合語(yǔ)音信號(hào)分離、圖象的消噪等方面。
??? 人體的心電信號(hào)在采集過(guò)程中,由于儀器、人體等內(nèi)外環(huán)境的影響,不可避免地混雜了各種干擾信號(hào),如工頻干擾、人工偽跡、基線漂移和肌電干擾等。這些噪聲干擾與心電信號(hào)混雜,會(huì)引起心電信號(hào)的畸變,使心電波形模糊不清, 從而影響信號(hào)特征點(diǎn)的識(shí)別,難以分析和診斷,因此有效分離各種干擾信號(hào)對(duì)心電信號(hào)處理有著重要的意義[2]。在論文中,將采用ICA方法對(duì)心電信號(hào)進(jìn)行分析處理,消除干擾信號(hào)。
1 ICA基本理論
1.1 ICA 模型
??? 假設(shè)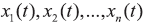 是一組N維的觀測(cè)信號(hào),
是一組N維的觀測(cè)信號(hào),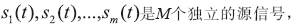 源信號(hào)通過(guò)混合以后得到觀測(cè)信號(hào),如式(1)所示:
源信號(hào)通過(guò)混合以后得到觀測(cè)信號(hào),如式(1)所示:
???  素表示源信號(hào)之間的線性混合情況。
素表示源信號(hào)之間的線性混合情況。
??? 獨(dú)立分量分析就是在源信號(hào)S及混合矩陣A未知的情況下,通過(guò)求得一M×N的解混矩陣W,使得通過(guò)它可以僅從觀測(cè)信號(hào)X來(lái)恢復(fù)出源信號(hào)S。其中y為源信號(hào)的估計(jì)矢量:????????
???? ???????????????????
???????????????????
??? ICA原理如圖1所示。
?
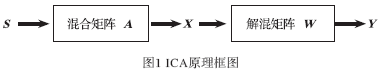
??? 對(duì)于以上描述的ICA模型,由于源信號(hào)S和線性組合方式A均未知,如果沒(méi)有任何先驗(yàn)知識(shí),要想僅從觀測(cè)信號(hào)恢復(fù)出源信號(hào)是不可能的。為使問(wèn)題可解,一般做如下假設(shè):
??? (1)各源信號(hào)之間相互統(tǒng)計(jì)獨(dú)立;(2)源信號(hào)間的混合方式是線性的;(3)信號(hào)中最多只允許有一個(gè)高斯信號(hào),因?yàn)槎鄠€(gè)高斯信號(hào)的線性混合仍然服從高斯分布,從而導(dǎo)致信號(hào)不可區(qū)分;(4)觀測(cè)信號(hào)的數(shù)目不能小于獨(dú)立信號(hào)源的數(shù)目,一般討論兩者相等的情況;(5)源信號(hào)的各分量均值均為零。
??? 而且,y只是在滿足上述條件下對(duì)S的逼近。換句話說(shuō),ICA算法任務(wù)的實(shí)質(zhì)是優(yōu)化問(wèn)題。因此ICA方法的具體實(shí)現(xiàn)主要包括兩個(gè)方面,確定優(yōu)化判據(jù)即目標(biāo)函數(shù)以及選擇優(yōu)化算法。
??? 目標(biāo)函數(shù)通常也稱為對(duì)比函數(shù)或代價(jià)函數(shù)。目標(biāo)函數(shù)的定義主要是確定分析的目標(biāo)和建立判斷是否獨(dú)立的判據(jù)。ICA方法的判別依據(jù)根據(jù)度量各分量之間獨(dú)立程度的判據(jù)不同, 有多種形式。如信息最大化(info-max)方法、最大熵(ME)和最小互信息(MMI)方法、極大似然(ML)法及快速ICA(fastICA)方法等。其中FastICA算法使用方便,程序編寫也比較成熟,應(yīng)用較多[3]。對(duì)于同一個(gè)目標(biāo)函數(shù)亦可以有不同的優(yōu)化算法。常見的優(yōu)化算法主要有梯度法和牛頓迭代法。
1.2 FasICA算法
??? FasICA又稱為固定點(diǎn)(Fixed-Point)算法,是一種基于負(fù)熵或極大似然估計(jì)等獨(dú)立性判決準(zhǔn)則的分離算法。與普通的神經(jīng)網(wǎng)絡(luò)算法不同的是,這種算法采用了批處理的方式,即在每一步迭代中都存在大量的樣本參與運(yùn)算。另外,該算法采用了定點(diǎn)迭代(Fixed-Point Iteration)的優(yōu)化方式,使得收斂速度快且穩(wěn)健[4-5]。
??? 使用FasICA算法分離單個(gè)獨(dú)立分量時(shí),首先進(jìn)行白化處理,使X的相關(guān)矩陣E[XXT]=1,即令X=BS,其中B是混合矩陣,其列向量是正交的。再考慮用kurtosis作為對(duì)比函數(shù),從而使得kurtosis達(dá)到最大化得到W(W=BT)。其對(duì)比函數(shù)如下:
??? 
??? 其中,w?=Wi(為W一行),且||?W||=1
??? 具體實(shí)現(xiàn)過(guò)程如下:
??? (1)初始化權(quán)值向量W(0),令||W(0)||?=1,k=1;
??? (2)迭代運(yùn)算:w(k)=E[x(W(k-1)Tx3]-3W(k-1),W=(bj)且||W||?=1,bj為B的第j列,其中數(shù)學(xué)期望可以用X的大量樣本點(diǎn)的均值代替;
??? (3)將W(k)標(biāo)準(zhǔn)化,即W(k)/||?W(k)||;
??? (4)如果W(k)TW(k-1)不是足夠地接近1,令k=k+1,返回步驟2,否則輸出向量W(k)。算法最后給出的向量W(k)意味著分離了混合信號(hào)x(k)中的一個(gè)非高斯信號(hào)W(k)Tx(k),其中k=1,2…等于其中的一個(gè)源信號(hào)[6-7]。
??? 對(duì)于多個(gè)獨(dú)立分量,可重復(fù)使用上述過(guò)程進(jìn)行分離,但每提取出一個(gè)獨(dú)立分量后,要從觀測(cè)信號(hào)中減去這一獨(dú)立分量,如此重復(fù),直到所有獨(dú)立分量完全分離。
??? 與其他ICA算法相比,F(xiàn)astICA有以下優(yōu)點(diǎn):(1)立方收斂,相比普通的基于梯度下降方法的線性收斂,收斂速度更快;(2)不需要選擇學(xué)習(xí)步長(zhǎng)或其他參數(shù),更易使用;(3)不管是具有超高斯分布還是亞高斯分布的分量都能被提取出來(lái);(4)獨(dú)立成分可以逐個(gè)估計(jì),在僅需要估計(jì)幾個(gè)(不是全部)獨(dú)立分量的情況下,能減少計(jì)算量。(5)FastICA還有許多神經(jīng)算法的優(yōu)點(diǎn),如并行、計(jì)算簡(jiǎn)單、要求的內(nèi)存少等。
2 ICA在心電信號(hào)處理中的應(yīng)用
??? 工頻干擾是由電力系統(tǒng)引起的一種干擾,由50Hz及其諧波構(gòu)成,是心電信號(hào)中最常見的干擾源之一。可以說(shuō)消除工頻干擾是心電信號(hào)檢測(cè)與處理過(guò)程中最經(jīng)典的話題。
??? 由于心電信號(hào)和工頻干擾信號(hào)可以被看成是由不同的相對(duì)獨(dú)立的源產(chǎn)生的,因此可以認(rèn)為它們之間是相互獨(dú)立的,觀測(cè)到的信號(hào)混合方式是線性的;嚴(yán)格地說(shuō)心電信號(hào)及這些干擾信號(hào)都不是高斯信號(hào),這樣就滿足了ICA的前3個(gè)條件,對(duì)于第4個(gè)條件,可以通過(guò)增加通道數(shù)目來(lái)滿足。因此在實(shí)驗(yàn)中,可以利用ICA算法來(lái)分離源信號(hào),消除工頻干擾。
??? 工頻干擾的數(shù)學(xué)模型可表示為:
??? 
??? 其中,A, f, θ分別為工頻干擾的幅值、頻率以及相位。f為50?Hz,而A, θ為未知的參數(shù),且θ通常較難估計(jì)。利用sin(2π?f?)和cos(2π?f??)的線性組合可以得到任何相位的正弦信號(hào),因此用一個(gè)正弦信號(hào)s1(t)=sin(2π?ft)和一個(gè)余弦信號(hào)s2(t)=cos(2π?ft)正交來(lái)構(gòu)造工頻干擾源。
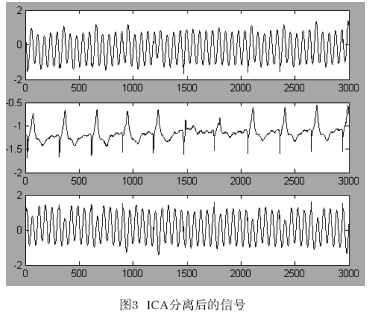
??? 圖2為原始心電信號(hào)(數(shù)據(jù)來(lái)源于MIT-BIH Arrhythmia Database,采樣個(gè)數(shù)為3?000)以及所構(gòu)造的工頻干擾信號(hào)。將這三路信號(hào)混合后的觀測(cè)信號(hào)作為FastICA算法的輸入,即可分離出相應(yīng)的工頻干擾,分離結(jié)果如圖3所示。
?

?
?
??? 比較源信號(hào)以及經(jīng)過(guò)ICA分離后的信號(hào)圖,可以看到,分離出的信號(hào)除了波形的次序、極性和波幅發(fā)生變化之外,源信號(hào)的波形被很好地分解出來(lái),能比較真實(shí)地反映源信號(hào)。可見,利用ICA方法能成功地將工頻干擾消除,在沒(méi)有破壞原有有用信息的基礎(chǔ)上,還能使某些特征由于干擾的消除變的更明顯。??? 本文將ICA方法應(yīng)用于心電信號(hào)干擾消除過(guò)程,成功分離出干擾信號(hào),較好地保留了原始心電信號(hào)中的細(xì)節(jié)信息,且不受信號(hào)頻譜混迭的限制,具有良好的效果。實(shí)驗(yàn)證明獨(dú)立分量分析方法是一種有效可行的信號(hào)分離方式,必將得到生物醫(yī)學(xué)信號(hào)處理領(lǐng)域的廣泛應(yīng)用。
??? 但作為一種新的信號(hào)處理技術(shù),ICA理論體系并不完善,一些實(shí)際問(wèn)題還有待于進(jìn)一步解決。如分析各獨(dú)立分量時(shí)在很大程度上依賴于人的經(jīng)驗(yàn),各分量的輸出次序不確定,觀測(cè)數(shù)目如果小于信號(hào)源數(shù)目的情況以及信號(hào)源非線性混合等情況都還需要繼續(xù)研究。
參考文獻(xiàn)
[1]?賈金玲,姚 毅,陳志利. 基于ICA的盲信號(hào)分離算法研究[J].四川理工學(xué)院學(xué)報(bào)(自然科學(xué)版),2007,20(2):72-76.
[2]?劉清欣,萬(wàn) 紅. 基于獨(dú)立分量分析的胎兒心電信號(hào)提取[J].華北水利水電學(xué)院學(xué)報(bào),2007,28(3):45-47.
[3]?游榮義,陳 忠. 一種基ICA的盲信號(hào)分離快速算法[J].電子學(xué)報(bào), 2004,4(4):669-672.
[4]?Hyvarinen A. Fast and robust fixed-point algorithms for independent component analysis[J]. IEEE Trans. on Neural Networks,1999, 10 (3): 626-634.
[5]?Cardoso J F. High-order contrasts for independent component analysis[J].Neural Computation, 1999,11(1):157-192.
[6]?楊福生,洪 波,唐慶玉. 獨(dú)立分量分析及其在生物醫(yī)學(xué)工程中的應(yīng)用[J].國(guó)外醫(yī)學(xué)生物醫(yī)學(xué)工程分冊(cè),2000,23(3):129-134.
[7]?吳小培,馮煥清,周荷琴,等.獨(dú)立分量分析及其在腦電信號(hào)預(yù)處理中的應(yīng)用[J].北京生物醫(yī)學(xué)工程, 2001,20(1):35-37.

