摘  要： 將多模型綜合的思想和“變點(diǎn)”思想相結(jié)合，給出了一種簡單有效且具有普適性的軟件可靠性預(yù)測方法——基于模糊隸屬度的軟件可靠性多模型綜合預(yù)測方法,。首先闡述了多模型綜合預(yù)測問題的一般描述,，并介紹了模型評價(jià)準(zhǔn)則，然后給出了單個模型權(quán)重的確定方法和該方法的一般步驟,，最后用實(shí)際數(shù)據(jù)驗(yàn)證了方法的有效性及普適性,。
關(guān)鍵詞： 軟件可靠性；模糊隸屬度,；多模型綜合

　軟件的普遍應(yīng)用促進(jìn)人們對其可靠性的關(guān)注,，到目前為止軟件可靠性的研究取得了很大的成果，提出了近百種軟件可靠性預(yù)測模型,，如JM模型,、GO模型、NHPP模型,、LV模型等,，并稱此類模型為經(jīng)典模型。但是單個經(jīng)典模型存在很大的局限性,，對于一個軟件可靠性的評估往往很難用一個模型來處理,，而且很多軟件可靠性模型都是建立在概率分布假設(shè)的基礎(chǔ)上，這就造成對一個軟件有很好的適用性而對其他的軟件則效果很差[1],。20世紀(jì)90年代以來,，基于知識的方法被越來越多地應(yīng)用到軟件可靠性預(yù)測中，如神經(jīng)網(wǎng)絡(luò)的方法[2-4],、遺傳算法,、支持向量機(jī)、泛函網(wǎng)絡(luò)等。然而這些方法算法復(fù)雜,、計(jì)算性能較低,、其預(yù)測結(jié)果的精確性取決于神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)的設(shè)計(jì)和模型的訓(xùn)練。Cai[5]在大量對比實(shí)驗(yàn)的基礎(chǔ)上指出,，大多數(shù)情況下,，神經(jīng)網(wǎng)絡(luò)方法很難得出滿意的量化預(yù)測結(jié)果。
　由于單個經(jīng)典模型的局限性以及基于新理論方法的復(fù)雜性和不成熟性,，軟件可靠性預(yù)測仍然還有很多問題需要解決：一是建立能夠普遍應(yīng)用的模型,；二是設(shè)計(jì)一套行之有效的模型選擇方法，能夠讓工程人員從眾多的軟件可靠性模型中選擇出最適合實(shí)施項(xiàng)目的模型,。
　Littlewood B在對大量軟件項(xiàng)目研究的基礎(chǔ)上提出了“變點(diǎn)”的思想[6]，表明不能期望用某一個模型來描述軟件的失效過程,，而從另一個側(cè)面表明可以用多個模型來描述軟件的失效過程,。香港中文大學(xué)的Lyu Michael提出了多個單一經(jīng)典模型“綜合”的思想[1]，并提出了四種線性“綜合”的方法,，試圖找到一種能夠普遍適用的軟件可靠性預(yù)測方法,。
　本文將多模型綜合思想和“變點(diǎn)”思想相結(jié)合，提出了一種基于模糊隸屬度的軟件可靠性多模型綜合預(yù)測方法,，通過各個經(jīng)典模型的預(yù)測數(shù)據(jù)和實(shí)際數(shù)據(jù)的模糊等于程度來動態(tài)地改變單個模型的權(quán)重,，以綜合各個模型的優(yōu)勢，進(jìn)而更準(zhǔn)確地預(yù)測軟件的可靠性,。


2.1.3 單個經(jīng)典模型權(quán)重的計(jì)算方法
　在進(jìn)行軟件可靠性線性綜合模型動態(tài)預(yù)測時(shí),，單個經(jīng)典模型權(quán)重的確定是最重要的。本文給出動態(tài)計(jì)算單個經(jīng)典模型權(quán)重的方法步驟如下：
　(1)在二元信息表的基礎(chǔ)上,，選擇前h個時(shí)刻作為基礎(chǔ)數(shù)據(jù)(前h個時(shí)刻的實(shí)際失效數(shù)已知),。
　(2)計(jì)算前h個時(shí)刻每個模型預(yù)測失效數(shù)和實(shí)際失效數(shù)的模糊等于程度A(cit)。
　(3)計(jì)算出各個模型在對h+1時(shí)刻軟件失效數(shù)預(yù)測的重要度(即權(quán)值)Wci：

　
　(5)當(dāng)實(shí)際測得t+1時(shí)刻的失效數(shù)d′t+1后,，二元關(guān)系表指針下移一位(即t=t+1),，返回第三步。
3 綜合模型評價(jià)
　對軟件可靠性模型預(yù)測性能進(jìn)行評價(jià)最主要的是模型的有效性,，它可以用定量的方法來測量,。本文采用的評價(jià)標(biāo)準(zhǔn)如下：
　(1)平均誤差A(yù)E(Average Error)[7]：在整個測試階段模型預(yù)測的誤差均值，只能針對同一數(shù)據(jù)進(jìn)行比較,。平均誤差越小,，模型的預(yù)測效果越好。
　(2)平均偏差A(yù)B(Average Bias error)[7]：在整個測試階段模型預(yù)測總的偏差趨勢,。平均偏差越接近于零,，模型的預(yù)測效果越好。
　(3)均方根誤差RMSE(Root Mean Square Error)[1]：在整個測試階段模型預(yù)測值和實(shí)際值距離,。均方根誤差值越小,，模型的擬合度越高,，預(yù)測性能越好。
4 實(shí)驗(yàn)分析
4.1 實(shí)驗(yàn)1
　選取UDIMM(University of Denmark Informatics and Mathematical Modeling)提供的數(shù)據(jù)包[8]中一軟件失效數(shù)據(jù)作為實(shí)例進(jìn)行預(yù)測分析,。根據(jù)Lyu所提出的幾個經(jīng)典模型選擇原則,，選用JM、GO,、LV,、YO四個經(jīng)典模型。其中,，JM模型是馬爾可夫過程模型,，GO模型和YO模型都是經(jīng)典的非齊次泊松過程模型，LV模型是貝葉斯模型,，它們都有很好的預(yù)測效果并且應(yīng)用比較廣泛,。四個模型預(yù)測偏好的綜合正好可以相互抵消，GO,、LV模型的預(yù)測結(jié)果比較樂觀,，而JM模型和YO模型的預(yù)測結(jié)果則有悲觀也有樂觀。
　設(shè)固定窗口h=4,，即采用前4個時(shí)刻各個經(jīng)典模型的預(yù)測失效數(shù)和實(shí)際失效數(shù)建立二元關(guān)系表,。使用基于模糊隸屬度的軟件可靠性多模型動態(tài)綜合預(yù)測方法步驟進(jìn)行計(jì)算，隸屬函數(shù)參數(shù)δ=0.25時(shí)計(jì)算結(jié)果如表1所示,。

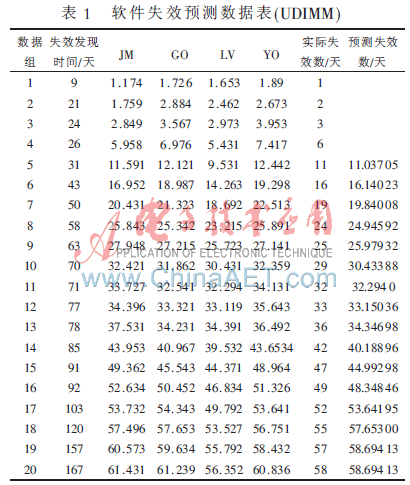
　從表1可以看出,，該失效數(shù)據(jù)存在“變點(diǎn)”的問題，即在第5~第7個時(shí)刻,，JM和LV模型比較適用,；從第7個時(shí)刻開始一直到第12個時(shí)刻，LV模型比較適用,，GO模型次之,，此后都沒有特別合適的模型?；谀：`屬度的軟件可靠性多模型動態(tài)綜合預(yù)測方法能夠動態(tài)地對各時(shí)刻各分模型的權(quán)重進(jìn)行調(diào)整,，使得整個測試過程中對失效數(shù)的預(yù)測都比較準(zhǔn)確；而且采用固定窗口滑動步長,，能夠很好地感知數(shù)據(jù)的變化,，減小了數(shù)據(jù)噪聲。
為了與單個模型的預(yù)測性能進(jìn)行對比,，選用平均誤差(AE),、平均偏差(AB)、均方根誤差(RMSE)作為模型預(yù)測性能的評價(jià)標(biāo)準(zhǔn)。各個模型評價(jià)標(biāo)準(zhǔn)計(jì)算結(jié)果如表2所示,。表中FD模型即是本文提出的基于模糊隸屬度的軟件可靠性多模型動態(tài)綜合預(yù)測方法,。

　從表2可以看出，F(xiàn)D模型的絕大多數(shù)評價(jià)標(biāo)準(zhǔn)值都比單個模型的好,，只有δ=0.5的FD模型預(yù)測結(jié)果的均方根誤差較大,，說明FD模型比單個經(jīng)典模型有更好的預(yù)測性能。δ=0.25時(shí),，F(xiàn)D模型的三個評價(jià)標(biāo)準(zhǔn)取值比δ=0.5時(shí)好很多,，也更合理；說明δ=0.25時(shí)隸屬函數(shù)能夠更好地描述模糊等于這個概念,，更能反映客觀實(shí)際情況,，即是把更大的權(quán)重分配給預(yù)測值更貼近實(shí)際失效數(shù)的模型。當(dāng)δ過于小時(shí),，綜合預(yù)測時(shí)會過于偏重某一個經(jīng)典模型,，不能夠達(dá)到綜合多個模型優(yōu)勢的效果。
4.2 實(shí)驗(yàn)2
　為了與Lyu提出的動態(tài)權(quán)重的線性綜合模型(DLC)進(jìn)行比較,，選取Musa發(fā)表的DACS數(shù)據(jù)集合中的一組失效數(shù)據(jù)(SYS1)[8]和Lyu提供的一組軟件項(xiàng)目失效數(shù)據(jù)(LDATA)[9]進(jìn)行試驗(yàn)。同樣選用Lyu選擇的三個經(jīng)典模型：GO模型,、MO模型,、LV模型，固定窗口h=4,，隸屬函數(shù)參數(shù)取0.25,。分別用兩種方法對兩組數(shù)據(jù)進(jìn)行預(yù)測，并對模型預(yù)測性能進(jìn)行評價(jià),。兩種方法的評價(jià)標(biāo)準(zhǔn)計(jì)算結(jié)果如表3所示,。

　從表3可以看出，本文的FD模型在各個標(biāo)準(zhǔn)下都優(yōu)于DLC模型,。這主要是因?yàn)镈LC模型是根據(jù)模型的累積預(yù)測精確度來動態(tài)確定權(quán)重,，這樣平滑了預(yù)測時(shí)刻以前所有的基礎(chǔ)數(shù)據(jù)，不能很好地反映“變點(diǎn)”的思想,；而FD模型采用固定窗口滑動步長來動態(tài)確定權(quán)重,，能夠敏銳地感知數(shù)據(jù)的變化，及時(shí)調(diào)整權(quán)重,，又不至于平滑過量的基礎(chǔ)數(shù)據(jù),，從而取得更好的預(yù)測效果。
　本文提出的基于模糊隸屬度的軟件可靠性多模型動態(tài)綜合預(yù)測方法結(jié)合“變點(diǎn)”思想,，采用模糊隸屬的方法來動態(tài)確定單個模型在綜合預(yù)測時(shí)的權(quán)重,，以期獲得更準(zhǔn)確的預(yù)測效果。從實(shí)驗(yàn)可以看出，該方法不但比單個經(jīng)典模型有更高的預(yù)測精度和更好的預(yù)測效果,，而且比Lyu提出的線性綜合模型更能反映動態(tài)反應(yīng)軟件失效數(shù)據(jù)中“變點(diǎn)”的問題,，有更高的預(yù)測精度和更好的預(yù)測效果。該方法對多個軟件項(xiàng)目具有普適性,，而且簡單有效,，在一定程度上解決了一個模型只對某個軟件工程項(xiàng)目或者其中某一段時(shí)間能夠達(dá)到較高的預(yù)測水平的問題。
參考文獻(xiàn)
[1] LYU M R,， NIKORA A. Applying reliability models more effectively[J]. IEEE Software,， 1992， 9(4)：43-52.
[2] KARUNANITHI N,， WHITLEY D,， MALAIYA Y K.  Using neural networks in reliability prediction[J]. IEEE Software， 1992,， 9(4)：53-59.
[3] SITTE R. Compareson of software-reliability-growth predictions： neural networks vs parametric-recalibration[J]. IEEE Trasactions on Reliability,， 1999， 48(3)：285-291.
[4] Su Yushen,， Huang Chinyu. Neural-network-based approaches for software reliability estimation using dynamic weighted combinational models[J]. Journal of Systems and Software,， 2007， 80(4)：606-615.
[5] CAI K Y,， CAI L,， Wang Weidong， et al. On the neural network approach in software reliability modeling[J]. The Journal of Systems and Software,， 2001,， 58(1)：47-62.
[6] PHAME H. Reliability handbook[S]. NewYork： Springer Verlag， 2002.
[7] MALAIYA Y K,， KARUNANITHI N. Predictability measures for software reliability models[C]. Fourteenth Annual International Computer Software and Applications Conference,，
1990COMPSAC 90. 1990， 1：7-12.
[8] VLADICESCU F P. Performance evaluation of computers courses technical,， University of Denmark Informatics and Mathematical Modeling. http：//www.imm.dut.dk/popentiu/pec/pec.html.(2009-04-06).
[9] LYU M R,， NIKORA A. CASRE-A computer-aided software reliability estimation tool[C]. Computer-Aided Software Engineering Proceedings. 1992：264-275.