隨著科學(xué)技術(shù)和生產(chǎn)的迅猛發(fā)展,，各個領(lǐng)域?qū)ψ詣涌刂频囊蟛粩嗵岣撸詥渭償?shù)學(xué)解析結(jié)構(gòu)為基礎(chǔ)的控制理論,，其局限性日益明顯,，對于一些大型,、復(fù)雜和不確定的對象，難以用精確的數(shù)學(xué)模型描述,。即使一些對象能夠建立起數(shù)學(xué)模型,，結(jié)構(gòu)也往往十分復(fù)雜，難于設(shè)計和實(shí)現(xiàn)有效控制,。近年來十分熱門的自適應(yīng),、自校正控制雖然能在一定程度上解決不確定性問題，但其本質(zhì)上仍然要求對象模型的在線辨識,，故算法復(fù)雜,、運(yùn)算量大，應(yīng)用范圍受到限制,。實(shí)際上,，任何一個有效的工業(yè)控制設(shè)計，都不能由控制理論單獨(dú)解決,，都隱含著人的直覺推理,。原有控制理論單純的數(shù)學(xué)結(jié)構(gòu)難以處理有關(guān)對象的一些定性信息，而單純運(yùn)用人的經(jīng)驗(yàn)知識,、技巧和直覺推理,，也難以滿足對復(fù)雜控制系統(tǒng)的設(shè)計要求,。
　　假如將人的經(jīng)驗(yàn)知識、技巧和直覺推理與控制理論相結(jié)合,，把它作為控制理論解決復(fù)雜生產(chǎn)過程的一個補(bǔ)充手段,，將使控制理論解決復(fù)雜生產(chǎn)過程有一個突破性進(jìn)展。這種將人的經(jīng)驗(yàn)知識直接參與生產(chǎn)過程的控制系統(tǒng),，稱為智能控制系統(tǒng),。
　　無毒提金工藝過程是一個復(fù)雜的物理化學(xué)過程，由于這一工藝過程千變?nèi)f化,，干擾不同,，對各個參數(shù)的要求不盡相同。如果控制模型過于簡單,，則導(dǎo)致系統(tǒng)超調(diào)量大,、調(diào)節(jié)時間長，造成各個參數(shù)不穩(wěn)定,，這些都嚴(yán)重影響無毒提金工藝的生產(chǎn)效率的提高,。因而，國內(nèi)外學(xué)者對無毒提金工藝及設(shè)備的自動控制曾做了大量工作,，以期能實(shí)現(xiàn)低能耗和高效率的目標(biāo),。常用的控制方案歸結(jié)起來不外乎以下幾種：
　　(1)自適應(yīng)控制(包括模型參考自適應(yīng)控制和自校正控制)方案；
　　(2)最優(yōu)控制方案,；
　　(3)PID控制(包括各種變型PID控制)方案,。
　　自適應(yīng)控制方案從理論上講是較先進(jìn)的控制方案，但它基本上適用于工況比較穩(wěn)定的工藝過程,。而無毒提金工藝過程各參數(shù)相對很難穩(wěn)定,，各參數(shù)將在某一值附近頻繁變化，最需要有效的控制,。否則,，對無毒提金攪拌設(shè)備控制的經(jīng)濟(jì)效果并不明顯，控制將無多大的意義,。
　　最優(yōu)控制方案是用得最多的一種方案,，它是在已知系統(tǒng)高階狀態(tài)方程后通過線性化和降階處理，得出一個較精確的低階狀態(tài)方程,，然后以快速性和系統(tǒng)超調(diào)作為控制性能指標(biāo),，應(yīng)用最大值原理，得出最佳控制規(guī)律,。這種控制策略在系統(tǒng)狀態(tài)方程精確已知時,，控制效果很好。
　　PID控制雖然控制方法較簡單,，但它在無毒提金攪拌設(shè)備各個控制參數(shù)變化比較頻繁的控制系統(tǒng)中較為實(shí)用,、可靠,。實(shí)踐經(jīng)驗(yàn)表明，在參數(shù)選擇合適的情況下,，PID控制性能幾乎同最優(yōu)控制效果一樣,，有些性能甚至更好些。PID控制需要檢測的參數(shù)全是電量,，而電量的檢測遠(yuǎn)比熱量,、溫度和化學(xué)成分的檢測容易得多，亦容易實(shí)現(xiàn),。但PID控制具有超調(diào)大,、參數(shù)較難確定、對擾動恢復(fù)慢等缺點(diǎn),。
　　綜合上述分析的種種情況,，針對無毒提金工藝過程的工況要求和各個參數(shù)的特點(diǎn)及存在的各種干擾情況，在深入分析其機(jī)理的基礎(chǔ)上,，將最優(yōu)控制,、模糊控制、PID控制結(jié)合在一起,，作者提出一種具有快速性和靈敏性的智能復(fù)合控制方案,。
　　該控制方案既對PID算法加以了改進(jìn)保留，如在傳統(tǒng)PID調(diào)節(jié)中加入新的微分積分作用,，對給定值與測量值變化造成的偏差分別采用不同的調(diào)節(jié)方式等，又加入了一些模糊調(diào)節(jié)算法的規(guī)則,。在偏差大時,，希望攪拌設(shè)備控制系統(tǒng)各控制參數(shù)能快速跟隨調(diào)整，而對控制精度要求相對降低,，所以擬采用快速PID控制方案,；當(dāng)偏差趨小時，為了減小超調(diào)量,，提高系統(tǒng)的控制精度,，擬采用模糊控制為主、最優(yōu)控制為輔的控制方案,。該控制方案具有超調(diào)小,、控制精度高、參數(shù)確定簡單,、對復(fù)雜對象控制效果較好等特點(diǎn),。
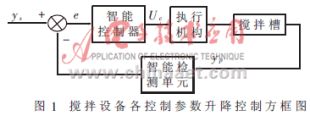
　　這就是智能復(fù)合控制的基本出發(fā)點(diǎn)，由此形成了圖1所示的閉環(huán)控制系統(tǒng),。功率控制實(shí)現(xiàn)功率曲線的自動跟蹤,，智能控制實(shí)現(xiàn)各控制參數(shù)的升降,。圖中y_s、y_p分別為各被控參數(shù)的設(shè)定值和實(shí)測值,，e為被控參數(shù)偏差,，e＝y(tǒng)_s－y_p。

　　各被控參數(shù)設(shè)定值由上位機(jī)或下位機(jī)給出,，具體方式有兩種：(1)根據(jù)經(jīng)驗(yàn)給出,；(2)根據(jù)無毒提金工藝要求計算確定。
1 智能控制器的實(shí)現(xiàn)
　　智能控制器的結(jié)構(gòu)框圖見圖2,，圖中y_s為被控參數(shù)的設(shè)定值,，y_p為被控參數(shù)的實(shí)測值，規(guī)則集用來判斷復(fù)合控制算法的轉(zhuǎn)換,，偏差信號e(k)＝y(tǒng)_s(k)－y_p(k),它作為智能控制器的輸入信號,。

　　限于篇幅，這里僅以PID控制為例,，簡單說明各控制算法的設(shè)計過程,。
　　按偏差的比例(proportional)、積分(integral),、微分(differential)控制(簡稱PID控制),，是過程控制中應(yīng)用最廣泛的一種控制算法。實(shí)際運(yùn)行經(jīng)驗(yàn)及理論分析表明,，這種控制算法對于大量的工業(yè)對象,，具有較好的調(diào)節(jié)性能和魯棒性，能夠達(dá)到符合原則的控制性能指標(biāo),。
　　在計算機(jī)控制系統(tǒng)中,，一般采用兩種控制算法：一種是含有理想微分的PID控制；另一種是含有實(shí)際微分的PID控制,。它們的控制原理,、實(shí)現(xiàn)方法、編程手段大同小異,。計算機(jī)控制是一種采樣控制,，它只能根據(jù)采樣時刻的偏差值計算控制量，因此需要將連續(xù)PID調(diào)節(jié)理想化,。
1.1 位置式PID控制算法

　　計算機(jī)按該式算出的是控制量的絕對數(shù)值,，即對應(yīng)于執(zhí)行機(jī)構(gòu)每次所應(yīng)達(dá)到的位置。在這種算法中,，如果前一次的輸出與過去的狀態(tài)有關(guān),，計算時要對e(i)進(jìn)行累加，計算機(jī)實(shí)現(xiàn)起來不夠方便,，不僅要占用較多的存儲單元,，而且不便于編程,。鑒于此，對(1)式要進(jìn)行改進(jìn),。
1.2 增量式PID控制算法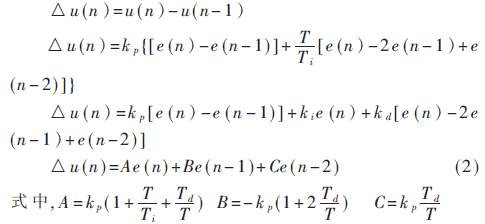

　　A,、B、C是與采樣周期T,、比例系數(shù)kp,、積分時間Ti、微分時間Td有關(guān)的系數(shù),，增量式算法只需要保持現(xiàn)時以前兩個時刻的偏差值即可,。
　　對于整個控制系統(tǒng)而言，上述兩種算法并無本質(zhì)上的區(qū)別,，只是所采用的執(zhí)行元件的特性不同,。增量式算法中將計算機(jī)的一部分任務(wù)：u＝∫△u分給了其它部件去承擔(dān)，即由執(zhí)行機(jī)構(gòu)完成,。增量式控制雖然只是在算法上做了一點(diǎn)改進(jìn),，但它帶來了不少優(yōu)點(diǎn)：
　　(1)計算機(jī)每次只輸出控制增量，故機(jī)器出現(xiàn)故障時,，影響范圍小,。
　　(2)控制從手動到自動轉(zhuǎn)換時，由于算法中不含有u0項,，因此沖擊小,。此外，當(dāng)計算機(jī)發(fā)生故障時,，由于執(zhí)行機(jī)構(gòu)裝置本身有鎖存作用,，故仍然能保持原值。
　　(3)算式中無需累加,，增量只是與最近幾次采樣值有關(guān)，編程簡單,，歷史數(shù)據(jù)可以遞推使用,，且占用存儲單元少，運(yùn)算速度快,，容易獲得較好的控制效果,。
　　但是，微分作用容易引入高頻干擾,，導(dǎo)致調(diào)節(jié)性能的不穩(wěn),。因此，在大量的工業(yè)控制系統(tǒng)中,，往往采用在微分調(diào)節(jié)器上串聯(lián)一個低通濾波器來抑制高頻干擾,。低通濾波器的傳遞函數(shù)為：
　　

　　也就是說,，利用實(shí)際微分來代替理想微分，輸出波形如圖3所示,。

　　這樣,，(2)式所示的增量式PID控制算式變?yōu)椋?BR>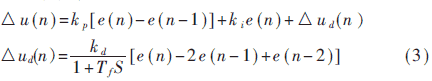　　
　　基于上述分析，在實(shí)際控制中,，增量式PID算法要比位置式PID算法應(yīng)用更為廣泛,。本攪拌設(shè)備自動控制系統(tǒng)就采用這種帶有低通濾波器的增量式PID控制算法，即：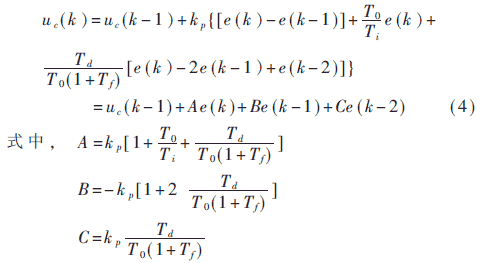

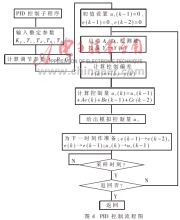
　　上式適合于計算機(jī)處理,，但式中的待定系數(shù)混合了PID控制的比例,、積分、微分加權(quán)系數(shù),，這將給系統(tǒng)調(diào)試階段,，依據(jù)運(yùn)行結(jié)果分析整定系數(shù)的習(xí)慣做法帶來諸多不便。實(shí)際應(yīng)用時,，為了兼顧調(diào)試和運(yùn)行兩方面的需要,，仍以K_p、T_i,、T_d為待整定參數(shù),。調(diào)試階段改變K_p、T_i,、T_d的取值后,，將新的一組K_p、T_i,、T_d值輸入計算機(jī),，然后由計算機(jī)程序利用有關(guān)公式計算出相應(yīng)的待定系數(shù)A、B,、C,。算法流程圖如圖4所示。

1.3 PID參數(shù)的整定
　　對于一個結(jié)構(gòu)和控制算法形式已定的控制系統(tǒng),，控制質(zhì)量的好壞主要取決于選擇的參數(shù)是否合理,。因此，PID控制中三個參數(shù)的選擇就顯得十分重要了,，整定PID參數(shù)的方法各式各樣,，有臨界比例度法、標(biāo)準(zhǔn)傳遞函數(shù)優(yōu)化法等等,。下面敘述兩種典型的整定方法,。
1.3.1 擴(kuò)充臨界比例度法
　　用實(shí)驗(yàn)參數(shù)進(jìn)行函數(shù)整定時，最常用的是擴(kuò)充臨界比例度法，它是整定模擬調(diào)節(jié)器參數(shù)的臨界比例度法的擴(kuò)充,。具體做法如下：
　?、龠x擇好采樣周期T₀;
　　②用與模擬調(diào)節(jié)器相同的臨界比例度法求出臨界比例系數(shù)Kk及臨界振蕩周期T_k;
　?、鄹鶕?jù)所選的控制度,，按經(jīng)驗(yàn)參數(shù)值表求出K_p、T_i,、T_d,。
1.3.2 Ziegler－Nichols整定規(guī)則
　　這是Roberts.P.D于1974年提出的，它只需整定一個參數(shù),，對于PID算式：
　　T₀＝0.1T_k;T_i＝0.5T_k;T_d＝0.125T_k(Ziegler－Nichols條件),，代入PID算式中，得：
　　u(k)＝u(k－1)+K_p[2.45e(k)－3.5e(k－1)+1.25e(k－2)]
　　整定時,，改變K_p的大小,，觀察控制效果，直到滿意為止,。當(dāng)然,，上述兩種方法只能提供一個粗略的范圍，實(shí)現(xiàn)過程中還得在這些數(shù)值的附近進(jìn)一步試探,，這樣才能找到最佳值,。
2 控制規(guī)則集的確定
　　由攪拌設(shè)備智能復(fù)合控制框圖可知，規(guī)則集用來判斷復(fù)合控制算法的轉(zhuǎn)換,。根據(jù)偏差e_i(e_i＝y(tǒng)_s－y_p)的變化組成控制規(guī)則集來實(shí)現(xiàn)智能控制,。具體控制規(guī)則可以按以下描述實(shí)現(xiàn)：
　　IF e_i＞ε THEN 　　u_c＝PID控制算法輸出；
　　IF e_i＜－ε THEN 　　u_c＝PID控制算法輸出,；
　　IF 0.5＜e_i≤ε THEN 　　u_c＝模糊控制算法輸出,；
　　IF －ε≤e_i＜－0.5 THEN 　　u_c＝模糊控制算法輸出；
　　IF 0.1＜e_i≤0.5 THEN　　u_c＝－U_M,，最優(yōu)控制算法
　　輸出,；
　　IF －0.5≤e_i＜－0.1 THEN 　　u_c＝+U_M，最優(yōu)控制算法
　　輸出,；
　　IF －0.1≤e_i≤0.1 THEN 　　u_c＝0,。
　　以上算法可用圖5表示。