橢圓曲線密碼系統(tǒng)(ECC)與其他公鑰加密系統(tǒng)相比，因其密鑰長度短,、安全強(qiáng)度高等諸多優(yōu)點(diǎn),，被公認(rèn)為最有前途的公鑰密碼體系,受到人們的普遍關(guān)注和研究[1-4]。

    在國內(nèi)外有關(guān)ECC的研究方面,，主要集中在 ECC的時(shí)間復(fù)雜度和空間復(fù)雜度上[2-4],。參考文獻(xiàn)[2]研究模逆和標(biāo)乘的快速算法,參考文獻(xiàn)[3]針對(duì)KP算法將改進(jìn)的Booth算法嵌入傳統(tǒng)算法，極大地降低了迭代次數(shù)和有限域運(yùn)算量,。參考文獻(xiàn)[4]將所有的模運(yùn)算全轉(zhuǎn)化為模乘運(yùn)算和模加運(yùn)算,，并改進(jìn)了LSD乘法器,利用該單元進(jìn)行模運(yùn)算,從而其硬件實(shí)現(xiàn)了具有面積小、速度快等優(yōu)點(diǎn),。目前國內(nèi)的密碼技術(shù)還是落后于國外,，特別是在生活應(yīng)用中，國內(nèi)的企業(yè)基本上是引用國外的密碼技術(shù)進(jìn)行二次開發(fā),。如果要將實(shí)現(xiàn)的橢圓曲線密碼系統(tǒng)應(yīng)用到實(shí)際中,，則需要通過系統(tǒng)集成芯片設(shè)計(jì)(SOC),，將FPGA上實(shí)現(xiàn)的橢圓曲線密碼系統(tǒng)集成實(shí)用性的加密芯片。一旦設(shè)計(jì)過程中所需的資源和條件不夠完善,，將導(dǎo)致加密芯片的制作難以實(shí)現(xiàn),。為此，本文借助Xilinx公司提供的強(qiáng)大的系統(tǒng)級(jí)硬件仿真工具System Generator[5],，研究并設(shè)計(jì)ECC加解密系統(tǒng),。
1 橢圓曲線密碼體制
    由于最終是要在硬件上實(shí)現(xiàn)橢圓曲線密碼體制[6]，所以本文選擇的有限域是特征為2的GF(2n),，選擇的橢圓曲線方程如式(1)所示,。
　 
   
    可見橢圓曲線密碼體制涉及到GF(2n)上的模加運(yùn)算、模乘運(yùn)算,、求逆運(yùn)算,，還有橢圓曲線的KP點(diǎn)乘運(yùn)算，下面對(duì)幾個(gè)主要算法進(jìn)行分析,。
1.1 GF(2n)域上的模乘運(yùn)算
    模乘模塊是整個(gè)設(shè)計(jì)中最關(guān)鍵的模塊,模乘的過程包括多項(xiàng)式相乘和取模兩個(gè)過程,。傳統(tǒng)的乘法器是將兩個(gè)m位操作數(shù)相乘，然后對(duì)其進(jìn)行f(x)求模,。這樣的缺點(diǎn)就是需要一個(gè)2m位的寄存器來存儲(chǔ)中間結(jié)果,勢(shì)必會(huì)浪費(fèi)資源,。本文采用全串行移位相加法來實(shí)現(xiàn)模乘運(yùn)算[6]。該算法只有簡單的移位和“異或”運(yùn)算,，但是需要大量的移位運(yùn)算,，如果A、B具有m位,，則需要進(jìn)行m-1次移位運(yùn)算,這是比較耗時(shí)的。但是本文使用的FPGA工作在61.44 MHz時(shí)鐘下,，m一般取值在200左右,，因此全串行移位相加法大概需要的是ns級(jí)的時(shí)間，而且全串行移位算法也是最節(jié)省資源的算法,。通過Modelsim仿真該模塊,得到圖1所示結(jié)果,。其中, clk是系統(tǒng)時(shí)鐘61.44 MHz；reset是系統(tǒng)復(fù)位信號(hào),；en是使能端口,；din是乘數(shù)輸入端口，低位在前,；dout是輸出結(jié)果,；rdy是輸出結(jié)果有效指示。

1.2 GF(2n)域上的模逆運(yùn)算
　    對(duì)于GF(2n)域上的模逆運(yùn)算,，當(dāng)今最有效的算法就是擴(kuò)展歐幾里德算法和基于費(fèi)馬定理的模逆算法,。擴(kuò)展歐幾里德算法用時(shí)會(huì)比基于費(fèi)馬定理的模逆算法用時(shí)短很多,，但是相應(yīng)地是以犧牲硬件資源為代價(jià)，在后面的點(diǎn)乘算法和最后的橢圓曲線密碼體制的實(shí)現(xiàn)耗用資源很大,。擴(kuò)展歐幾里德算法還要去另外設(shè)計(jì)一個(gè)多項(xiàng)式模塊,，而基于費(fèi)馬定理的模逆算法只需要反復(fù)調(diào)用先前做好的模乘模塊就行，再加上本文用的FPGA時(shí)鐘頻率本身就高,，因此本文選擇費(fèi)馬定理來做模逆算法,。通過Modelsim仿真該模塊,得到圖2所示結(jié)果。其中,，clk是系統(tǒng)時(shí)鐘61.44 MHz,；reset是系統(tǒng)復(fù)位信號(hào)；en是模逆使能,；din是輸入數(shù)據(jù),；a_inv是輸出結(jié)果；rdy是輸出結(jié)果有效指示,。

    選取參數(shù)：
    K=157E51751D89C66CBDF44596BF7F653876A18C4B12
40B85A;
    x=36B3DAF8A23206F9C4F299D7B21A9C369137F2C84
AE1AA0D;
    y=7658E73433B3F95E332932E70EA245CA2418EA0EF9
8018FB;
    b=2E45EF571F00786F67B0081B9495A3D95462F5DE0A
A185EC;
    f=800000000000000000000000000000000000000000000
201,。
    仿真結(jié)果：
    Cx=34EEC5768673E71B8CDC139FB8EB4ACD9989FAA
E1EC9EF1D;
    Cy=779097F490A2DA7A6B09A9518733B4817D5C21947
547D2A1。
2 System Generator搭建ECC加密系統(tǒng)
    System Generator是業(yè)內(nèi)領(lǐng)先的高級(jí)系統(tǒng)級(jí)FPGA開發(fā)工具,。其作用是借助FPGA設(shè)計(jì)高性能DSP系統(tǒng)并和Simulink實(shí)現(xiàn)無縫鏈接,，快速建模并自動(dòng)生成代碼[5]。System Generator最大的特點(diǎn)就是可利用Simulink建模和仿真環(huán)境來實(shí)現(xiàn)FPGA設(shè)計(jì),，無需了解和使用RTL級(jí)硬件語言,，讓DSP設(shè)計(jì)者能夠發(fā)揮基于FPGA的DSP的最大性能和靈活性，并縮短整個(gè)設(shè)計(jì)周期,。前文用FPGA實(shí)現(xiàn)了ECC的各個(gè)關(guān)鍵模塊,下面用先前生成的各個(gè)模塊代碼通過System Generator的黑盒子生成各自相應(yīng)的模塊,。再將這些模塊搭建成完整的ECC模塊，以便在Matlab工作空間中輸入相應(yīng)的參數(shù),、明文和相應(yīng)的使能端口就可以實(shí)現(xiàn)加密,；輸入相應(yīng)的參數(shù)、密文和相應(yīng)的使能端口就可以實(shí)現(xiàn)解密,。但是本文所涉及的參數(shù)較大,，輸入的過程很耗費(fèi)時(shí)間，因此本文將參數(shù)都固定在一個(gè)ROM中間,，只要控制相應(yīng)的使能信號(hào),，就可以達(dá)到一個(gè)加解密的模擬過程。
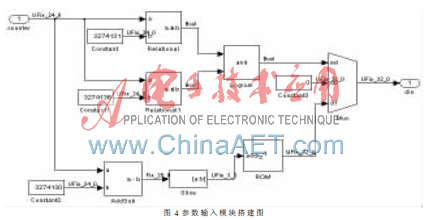
2.1數(shù)據(jù)輸入模塊的搭建
    本文中的端口有使能端口和參數(shù)端口,，其中,，使能端口是1 bit的，就可以用計(jì)數(shù)器來實(shí)現(xiàn),。對(duì)于191個(gè)bit位的參數(shù),，可先將其分解成6組的32 bit系數(shù),， 存在如圖4所示的ROM中，只要改變ROM中的值就可以控制輸入?yún)?shù)的值,，改變3個(gè)常數(shù)模塊就可以控制參數(shù)輸入的時(shí)刻,。

2.2 ECC系統(tǒng)的搭建與仿真結(jié)果
    利用代碼生成的KP模塊、求逆模塊和乘法模塊搭建成ECC加解密系統(tǒng),。由于ECC加解密系統(tǒng)的各個(gè)子模塊有很多的反饋端口,，搭建起來的圖顯得比較亂，因此可以在ECC系統(tǒng)中的m文件添加 this block.addFile(),。把各個(gè)子模塊添加到ECC頂層模塊中,這樣就相當(dāng)于把各個(gè)子模塊集成在統(tǒng)一的黑盒子中,。
    設(shè)置運(yùn)行時(shí)間為4 000 000個(gè)時(shí)鐘周期，將加解密指示信號(hào)設(shè)置為加密,，點(diǎn)擊運(yùn)行,，進(jìn)行加密仿真，在工作區(qū)間可以看到,，明文輸入和對(duì)應(yīng)的密文輸出,。例如，當(dāng)輸入的明文為“4129534493046158328227537522838960054530294419451055575666”時(shí),，輸出的密文為“3625519732263338515328819742424233936313311718087”,。
    設(shè)置運(yùn)行時(shí)間為4 000 000個(gè)時(shí)鐘周期，將加解密指示信號(hào)設(shè)置為解密,，點(diǎn)擊運(yùn)行,，進(jìn)行解密仿真，在工作區(qū)間可以看到密文輸入和對(duì)應(yīng)的的明文輸出,。例如,，當(dāng)輸入的密文為“362551973226333851532881974242423393631
3311718087”, 則輸出的明文為“4129534493046158328227537522838960054530294419451055575666”。
    ECC模塊加解密運(yùn)算輸出有效數(shù)據(jù)的時(shí)鐘周期是第3274550,，使能信號(hào)則是在第11個(gè)時(shí)鐘周期輸入,，因此整個(gè)運(yùn)算過程中數(shù)據(jù)的輸入輸出所耗費(fèi)的時(shí)間是3274550-11=3 274 539個(gè)時(shí)鐘周期，所以對(duì)于采用時(shí)鐘頻率為61.44 MHz的FPGA來說,，只要用3 274 539/61.44 ?滋s就可以完成一次加密算法，或者一次解密算法,?？偣灿玫臅r(shí)間為3274539/61.44 ns=53.3 ms，而若單單只用Matlab仿真運(yùn)行,，大概需要時(shí)間為20 min,。因此采用硬件實(shí)現(xiàn)橢圓曲線密碼系統(tǒng)的優(yōu)越性不言而喻。
參考文獻(xiàn)  
[1] HANKERSON D,，MENEZES A,， VANSTONE S． Guide to elliptic curve cryptography[M]． Springer Verlag New York Inc,，2004：25-147.
[2] MA S W， HAO Y L,， PAN Z Q． Fast  implementation for modular inversion an d scalar multiplication in the elliptic curve cryptography[C].IITA ’08,，Beijing，China,，2008:488-492.
[3] 龔書,，劉文江，戎蒙恬.一種橢圓曲線密碼加密算法及實(shí)現(xiàn)[J].高技術(shù)通訊,2004(3):25-28.
[4] 唐薛峰,沈海斌,，嚴(yán)曉浪.GF(2^m)上橢圓密碼體制的硬件實(shí)現(xiàn)[J].計(jì)算機(jī)工程與應(yīng)用,2004,，40(11)：96-98.
[5] 田耕，徐文波,，胡彬.Xilinx ISE Design Suite 10.x FPGA開發(fā)指南[M].北京：人民郵電出版社,2008.
[6] 祝躍飛,張亞娟.橢圓曲線公鑰密碼導(dǎo)引[M]. 北京：科學(xué)出版社,，2006.