摘  要： 針對(duì)復(fù)方作用特點(diǎn)，為提高臨床療效,，提出采用支持向量機(jī)SVM建模,、非支配排序遺傳算法NSGA-II多目標(biāo)優(yōu)化、熵權(quán)TOPSIS法多屬性決策優(yōu)選復(fù)方劑量配比的方法,，最后以苓桂術(shù)甘湯為例驗(yàn)證方法的有效性,。
關(guān)鍵詞： 復(fù)方配比；多目標(biāo)優(yōu)化,；支持向量機(jī),；非支配排序遺傳算法；熵權(quán)TOPSIS法

　實(shí)際優(yōu)化問(wèn)題大多數(shù)是多目標(biāo)優(yōu)化問(wèn)題MOP（Multi-Objective optimization Problems）,，多目標(biāo)優(yōu)化問(wèn)題最主要的特點(diǎn)是目標(biāo)間的矛盾性和不可共度性,，即一個(gè)目標(biāo)的改善可能會(huì)使得另一個(gè)目標(biāo)值變劣，目標(biāo)間一般沒(méi)有統(tǒng)一的度量標(biāo)準(zhǔn),，因而不能直接比較[1],。多目標(biāo)問(wèn)題的最優(yōu)解是一組最優(yōu)解的集合，稱為非劣解集,，即Pareto解集,。
　藥物研究中的許多問(wèn)題都是多目標(biāo)優(yōu)化問(wèn)題。例如,，在藥物的藥效評(píng)價(jià)研究中,，如何確定最佳方案，以使各治療效應(yīng)目標(biāo)都處于較好水平并且副作用相對(duì)最小等,。這樣的多目標(biāo)評(píng)價(jià)問(wèn)題在中藥制劑,、生產(chǎn)工藝、藥理和藥效中比比皆是,。在中藥復(fù)方藥物的研究中,，中藥復(fù)方的量效關(guān)系具有非線性特征，不同劑量的組方藥效可能存在著差異,，且中藥藥效具有多途徑,、多靶點(diǎn)特征[2]，選取不同的藥效指標(biāo)及指標(biāo)權(quán)重,，復(fù)方組分配比及組分間相互作用機(jī)制也不同,，因而有必要尋找能夠提升復(fù)方療效、使多個(gè)藥效指標(biāo)達(dá)到綜合最優(yōu)的藥味劑量,。本研究以苓桂術(shù)甘湯為例，采用遺傳算法優(yōu)化支持向量機(jī)建立量效關(guān)系多目標(biāo)優(yōu)化模型,，基于非支配排序遺傳算法進(jìn)行模型求解,，得出一組分配均勻的Paeto解，熵權(quán)法結(jié)合專家經(jīng)驗(yàn)確定指標(biāo)組合權(quán)重,，依據(jù)逼近于理想解的多屬性決策技術(shù)（TOPSIS）對(duì)Pareto方案排序并擇優(yōu),。
1 算法簡(jiǎn)介
1.1 支持向量機(jī)
　中藥復(fù)方量效關(guān)系是一個(gè)非線性,、確定的多變量輸入輸出關(guān)聯(lián)系統(tǒng)，涉及到的動(dòng)力學(xué)過(guò)程極為復(fù)雜,，很難用確定的數(shù)學(xué)模型來(lái)描述,。配比的多目標(biāo)優(yōu)化需要有可靠的、能夠反映各參數(shù)變化規(guī)律及相互作用關(guān)系的數(shù)學(xué)模型,。支持向量機(jī)SVM（Support Vector Machine）理論是一種專門研究有限樣本預(yù)測(cè)的學(xué)習(xí)方法,，具有嚴(yán)格的理論和數(shù)學(xué)基礎(chǔ)，是一種新型的結(jié)構(gòu)化學(xué)習(xí)方法,。它能很好地解決有限數(shù)量樣本的高維模型構(gòu)造問(wèn)題,，小樣本學(xué)習(xí)使它具有很強(qiáng)的泛化能力，且SVM算法是一個(gè)凸優(yōu)化問(wèn)題,，因此局部最優(yōu)解一定是全局最優(yōu)解,。其原理為：對(duì)于給定的樣本集{（xi，yi）|i=1,，2,，…，k},，其中xi為輸入向量,，yi為期望輸出，尋求一個(gè)樣本的最優(yōu)函數(shù)關(guān)系y=f（x）,，采用適當(dāng)?shù)暮撕瘮?shù)K（xi,，x）確定回歸模型[3]。
1.2 非支配排序遺傳算法
　非支配排序遺傳算法NSGA-II（Nondominated Sorting Genetic Algorithm）是帶精英策略的非支配排序遺傳算法,，它是Deb等人在NSGA的基礎(chǔ)上加入快速非支配排序算法,、引入精英策略、采用擁擠度和擁擠度比較算子發(fā)展起來(lái)的,，是一種基于Pareto最優(yōu)概念的遺傳算法,，是眾多的多目標(biāo)優(yōu)化算法中體現(xiàn)Goldberg思想最直接的方法[4]。傳統(tǒng)多目標(biāo)優(yōu)化方法將多目標(biāo)問(wèn)題轉(zhuǎn)化為單目標(biāo)問(wèn)題,，如綜合評(píng)分法,、綜合平衡法、線性加權(quán)法等,，此類方法只能找出一個(gè)Pareto最優(yōu)解,，且需要較多的專家經(jīng)驗(yàn)，而NSGA-II算法可以求出一組分布均勻的Pareto最優(yōu)解集,，用來(lái)逼近多目標(biāo)優(yōu)化問(wèn)題的所有Pareto最優(yōu)解,，為決策者提供了較多的備選方案。
1.3 熵權(quán)Topsis法
　熵是熱力學(xué)中重要概念，是物質(zhì)系統(tǒng)無(wú)序狀態(tài)的量度,，系統(tǒng)越亂,，熵就越大，系統(tǒng)越有序,，熵就越小,。將熵的概念引入信息論，則表示一個(gè)信息源發(fā)出的信號(hào)狀態(tài)的不確定程度[5],。中藥復(fù)方劑量配比研究中,，以往決策模型大部分只考慮決策者（專家）的主觀判斷權(quán)重，沒(méi)有體現(xiàn)決策目標(biāo)擁有的決策信息,。本研究采用熵值來(lái)度量所獲得決策信息,，將主觀權(quán)重與復(fù)方量效關(guān)系的客觀情況相結(jié)合，依據(jù)TOPSIS法求解最佳配比方案,。步驟[6]如下：


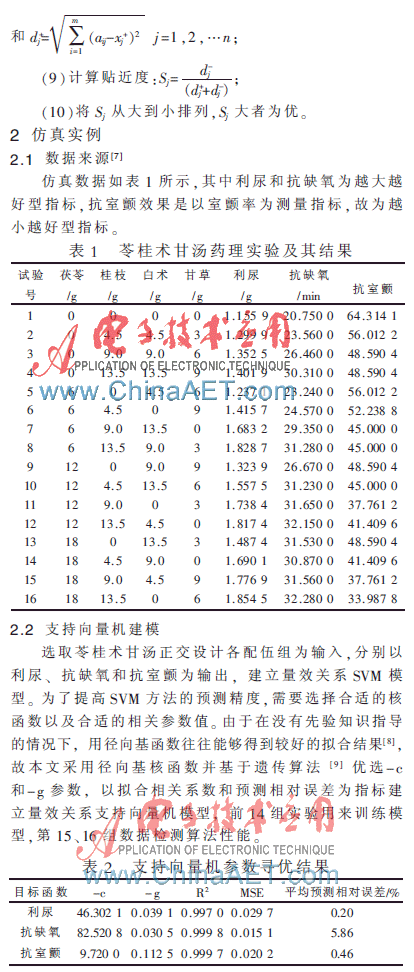
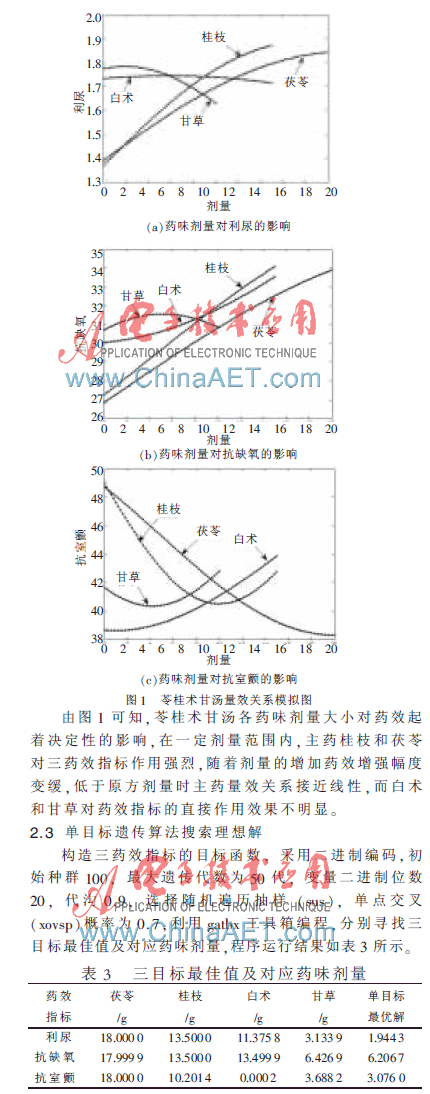
    由表2可知,，所建SVM模型對(duì)數(shù)據(jù)具有良好的擬合效果和預(yù)測(cè)效果，可用于多目標(biāo)優(yōu)化Pareto方案的求解,。分別控制其他藥味劑量為原方水平考察茯苓,、桂枝、白術(shù)和甘草對(duì)利尿,、抗缺氧和抗室顫三藥效指標(biāo)的影響,，結(jié)果如圖1所示。

    由圖2可以看出,，當(dāng)種群進(jìn)化到50代時(shí),，所得的Pareto最優(yōu)解具有良好的多樣性。這些解在不同的目標(biāo)上各占優(yōu)勢(shì),，決策者可以根據(jù)不同的偏好,，在這些解折中直接選擇，但直接選擇法具有較強(qiáng)的主觀隨意性,。研究者還可對(duì)優(yōu)化參數(shù)進(jìn)行限定并修改算法中的一些條件進(jìn)而使算法使用范圍得到拓展,，例如可將搜索范圍設(shè)置在藥效增加較快的水平等。
2.5 熵權(quán)TOPSIS法進(jìn)行Pareto方案排序
　在多目標(biāo)優(yōu)化獲得一組Pareto解后,，還需要對(duì)解集決策以挑選出基于方案的最優(yōu)解,。在Pareto最優(yōu)解集基礎(chǔ)上構(gòu)造決策矩陣，決策屬性定義為所考慮的3個(gè)目標(biāo)函數(shù),，因此決策矩陣的大小為500×3,。依據(jù)熵權(quán)法計(jì)算各指標(biāo)熵值分別為0.989 7、0.992 5和0.941 3,，熵權(quán)分別為 0.135 2,、0.097 4和0.767 3,，說(shuō)明抗室顫指標(biāo)在Pareto方案中所含信息量最大，是影響最佳配比選擇的主要因素,。主觀權(quán)重可由研究者根據(jù)臨床經(jīng)驗(yàn)及病人個(gè)體化差異確定，本研究將因子分析法[10]確定的三指標(biāo)權(quán)重作為主觀權(quán)重,，分別為0.332 8,、0.331 3、0.335 9,。按照TOPSIS方法對(duì)Pareto解進(jìn)行排序,，表4給出了貼近度從大到小的前10個(gè)方案。

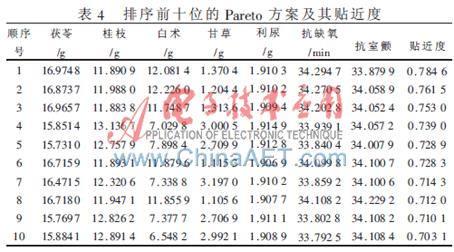
　以貼近度最大的方案為最終的優(yōu)化解,，得到：茯苓=16.974 8 g,，桂枝=11.890 9 g，白術(shù)=12.081 4 g,，甘草=1.370 4 g,。
3 討論
3.1 支持向量機(jī)參數(shù)的選擇
　SVM和大多數(shù)機(jī)器學(xué)習(xí)算法一樣，其性能的優(yōu)劣與參數(shù)和特征的選擇有關(guān),。不同的參數(shù)優(yōu)化方法其擬合和預(yù)測(cè)效果有一定的差異,。常用的參數(shù)優(yōu)化方法有網(wǎng)格搜索法[11]、粒子群優(yōu)化算法和遺傳算法[12-13],。本研究分別比較了三種參數(shù)優(yōu)化方法,，研究表明，網(wǎng)格搜索作為一種非啟發(fā)式搜索,，運(yùn)算量較大,，粒子群算法開(kāi)始尋優(yōu)迅速，但容易陷入局部最小,，而遺傳算法尋優(yōu)速度逐漸變快,，并且沒(méi)有陷入局部最小，可有效實(shí)現(xiàn)參數(shù)尋優(yōu),。
3.2 采用組合權(quán)重的優(yōu)點(diǎn)
　熵權(quán)并不是在決策問(wèn)題中某指標(biāo)實(shí)際意義上的重要性系數(shù),，而是在給定被評(píng)價(jià)方案集后各種評(píng)價(jià)指標(biāo)值確定的情況下，各指標(biāo)在競(jìng)爭(zhēng)意義上的相對(duì)激烈程度系數(shù),，只代表該指標(biāo)在該問(wèn)題中提供有用信息量的多寡程度,。單純采用熵權(quán)計(jì)算權(quán)重，屬性權(quán)重只能反映數(shù)據(jù)本身的特點(diǎn),，不能代表屬性的重要程度[14],。本文利用客觀熵權(quán)結(jié)合主觀專家權(quán)重的方法進(jìn)行組合賦權(quán)，可以有效地避免傳統(tǒng)方法中權(quán)重系數(shù)確定過(guò)程的主觀色彩,，同時(shí)更注重了評(píng)價(jià)體系指標(biāo)本身的重要程度,，充分利用了被評(píng)判指標(biāo)的信息量,，綜合權(quán)重既可以反映客觀的決策信息，又可以體現(xiàn)決策者對(duì)決策指標(biāo)的偏好,，因而使決策結(jié)果具有更高的準(zhǔn)確性和實(shí)用性,。
3.3 復(fù)方標(biāo)準(zhǔn)劑量的確定
　本研究中確定的苓桂術(shù)甘湯劑量不能作為標(biāo)準(zhǔn)劑量，由表3可知,，當(dāng)選取的藥效指標(biāo)不同時(shí),，其最佳劑量也不同。即使選擇相同的藥效指標(biāo),，研究者還應(yīng)根據(jù)病人的個(gè)體化差異靈活確定不同的主觀權(quán)重,，進(jìn)而從Pareto方案中擇優(yōu)。因此,，復(fù)方最佳劑量的確定應(yīng)結(jié)合不同的藥效指標(biāo)及臨床經(jīng)驗(yàn)共同確定,。
3.4 存在問(wèn)題及解決辦法
　由圖1可知，在一定范圍內(nèi),，藥效指標(biāo)隨著苓桂術(shù)甘湯各藥味劑量的增加改善不明顯,，即投入的劑量并未轉(zhuǎn)化為理想的藥效輸出。后續(xù)工作將采用數(shù)據(jù)包絡(luò)分析DEA（Data Envelopment Analysis）[15-16],，即將復(fù)方量效關(guān)系視為一個(gè)投入產(chǎn)出系統(tǒng),，藥效指標(biāo)的改善視為復(fù)方各藥味劑量投人轉(zhuǎn)化后的直接和間接產(chǎn)出，產(chǎn)出的多少不僅依賴于投入（藥味劑量）的多少,，還依賴于投入產(chǎn)出的效率,。擬采用基于投入的C2R模型以決策單元DMU（Decision Making Units）的效率評(píng)價(jià)指數(shù)θ、投入產(chǎn)出冗余松弛變量s+及s-進(jìn)行量效關(guān)系評(píng)價(jià),，計(jì)算投入產(chǎn)出比（研究結(jié)果將另文發(fā)表）,。
　支持向量機(jī)作為一種專門研究小樣本情況下機(jī)器學(xué)習(xí)規(guī)律的理論，比傳統(tǒng)的統(tǒng)計(jì)學(xué)習(xí)理論和神經(jīng)網(wǎng)絡(luò)具有更好的泛化推廣能力,，能夠很好地解決中藥復(fù)方量效關(guān)系非線性建模問(wèn)題,。非支配排序遺傳化算法作為一種模擬自然進(jìn)化過(guò)程的隨機(jī)優(yōu)化方法，同時(shí)也是一種全局性概率優(yōu)化方法,，用于多目標(biāo)優(yōu)化不僅可以一次性獲得大量Pareto最優(yōu)解,，而且其優(yōu)化結(jié)果具有良好的一致性。熵權(quán)TOPSIS法可在某種程度上反映決策指標(biāo)含有的信息的多少,，充分表現(xiàn)不同配比之間的指標(biāo)差異,，避免了決策過(guò)程的主觀性和盲目性。支持向量機(jī)建模,、非支配排序遺傳算法多目標(biāo)優(yōu)化,、熵權(quán)TOPSIS多屬性決策三者結(jié)合可較好解決復(fù)方劑量配比多目標(biāo)優(yōu)化問(wèn)題。
參考資料
[1] 張志剛,，馬光文.基于NSGA-II算法的多目標(biāo)水火電站群優(yōu)化調(diào)度模型研究[J].水力發(fā)電學(xué)報(bào),，2010,，29（1）：215-216.
[2] 田景振，王厚偉.基于中藥方劑的中藥多維組合藥物研究模式探討[J].山東中醫(yī)藥大學(xué)學(xué)報(bào),，2011,，35（2）：99- 101.
[3] 范玉妹，郭春靜.支持向量機(jī)算法的研究及其實(shí)現(xiàn)[J].河北工程大學(xué)學(xué)報(bào)：自然科學(xué)版,，2010,，27（4）：106-112.
[4] HERIS S M， KHALOOZADEHH. Open-and closed-loop multiobjective optimal strategies for HIV therapy using NSGA-II.[J]. IEEE Transaction Biomed Engineering,，2011，58（6）：1678-1685.
[5] 劉曉,，張宇.基于熵權(quán)和層次分析法的宿舍綜合評(píng)價(jià)[J].科學(xué)技術(shù)與程,，2011，11（2）：304-307.
[6] 王國(guó)全,，馮光文.熵權(quán)TOPSIS法在優(yōu)選低放射性裝飾建筑材料中的應(yīng)用[J].環(huán)境科學(xué)與管理,，2011，36（1）：22-25.
[7] 宋宗華,，馮東.苓桂術(shù)甘湯配伍機(jī)制及藥效物質(zhì)基礎(chǔ)研究[J].中成藥,，2003，25（2）：133-138.
[8] LIN H T,， LIN C J. A study on sigmoid kemels for SVM and the training of non-PSD kemels by SMO-type methods [EB],， 2003.
[9] 劉璐，劉愛(ài)倫.基于改進(jìn)的遺傳算法優(yōu)化支持向量機(jī)的精餾塔故障診斷[J].華東理工大學(xué)學(xué)報(bào)：自然科學(xué)版,，2011,，37（2）：228-233.
[10] 何君，石城,，楊思波,，等.基于因子分析和AHP的水資源可持續(xù)利用綜合評(píng)價(jià)方法[J].南水北調(diào)與水利科技，2011,，9（1）：75-79.
[11] 張向東,，馮勝洋，王長(zhǎng)江.基于網(wǎng)格搜索的支持向量機(jī)砂土液化預(yù)測(cè)模型[J].應(yīng)用力學(xué)學(xué)報(bào),，2011,，28（1）：24-28.
[12] 高昆侖，劉建明,，徐茹枝.基于支持向量機(jī)和粒子群算法的信息網(wǎng)絡(luò)安全態(tài)勢(shì)復(fù)合預(yù)測(cè)模型[J].電網(wǎng)技術(shù),， 2011，35（4）：176-182.
[13] 武海巍,，于海業(yè),，張蕾.基于參數(shù)優(yōu)化支持向量機(jī)的林下參凈光合速率預(yù)測(cè)模型[J].光譜學(xué)與光譜分析,， 2011，31（5）：1414-1418.
[14] 王國(guó)全,，馮光文.熵權(quán)TOPSIS法在優(yōu)選低放射性裝飾建筑材料中的應(yīng)用[J].環(huán)境科學(xué)與管理,，2011，36（1）：22-25.
[15] 張鵬,，秦毓毅,，唐茂林，等.基于數(shù)據(jù)包絡(luò)分析的水電企業(yè)節(jié)能調(diào)度效益評(píng)價(jià)[J].四川電力技術(shù),，2011,，34 （2）：91-94.
[16] MOUSAVI A S， RAFIEE S,， JAFARI A,， et al. Improving energy productivity of sunflower production using data envelopment analysis （DEA） approach[J]. J Sci Food Agric，2011,，91（10）：1885-1892.