摘  要： 為在低過(guò)采樣率下設(shè)計(jì)出高性能的調(diào)制器，通過(guò)采用級(jí)間反饋和1位AD/DAC與多位AD/DAC的混合設(shè)計(jì),，降低多位DAC非線性化而帶來(lái)的噪聲,，進(jìn)一步改善輸出信號(hào)的信噪比。提出了一種應(yīng)用于數(shù)字音頻放大器中的多位Σ-Δ調(diào)制器結(jié)構(gòu),。
關(guān)鍵詞： Σ-Δ調(diào)制器  數(shù)模轉(zhuǎn)換器  信噪比  過(guò)采樣率

　　隨著電子系統(tǒng)數(shù)字化的不斷深入,，人們對(duì)樂(lè)音信號(hào)回放的要求也越來(lái)越高，因此低失真,、高效率的D類放大器已成為研究的熱點(diǎn),。但目前D類放大器大多是使用模擬脈寬調(diào)制，如果要放大數(shù)字信號(hào),，還需要DAC將數(shù)字信號(hào)轉(zhuǎn)換成模擬信號(hào),。實(shí)際上，可以直接對(duì)數(shù)字音頻信號(hào)進(jìn)行數(shù)字脈寬調(diào)制來(lái)實(shí)現(xiàn)放大器的數(shù)字化[1],?；跀?shù)字脈寬調(diào)制的數(shù)字音頻放大器的基本結(jié)構(gòu)如圖1所示。數(shù)字幅值編碼信號(hào)（PCM）送入過(guò)采樣電路,，經(jīng)過(guò)Σ-Δ調(diào)制器進(jìn)行噪聲整形,，再經(jīng)過(guò)數(shù)字脈寬調(diào)制器調(diào)制成PWM脈寬信號(hào)，然后由PWM脈寬信號(hào)去控制功率轉(zhuǎn)換電路中的功率MOS管的開啟和關(guān)閉,，輸出的功率信號(hào)經(jīng)過(guò)低通平滑濾波器之后,，即可重建原來(lái)的模擬音頻信號(hào)。Σ-Δ調(diào)制器在數(shù)字音頻放大器中起著關(guān)鍵的作用,。在數(shù)字脈寬調(diào)制對(duì)數(shù)字信號(hào)進(jìn)行PWM調(diào)制的過(guò)程中,，由于PCM信號(hào)是對(duì)信號(hào)的幅值進(jìn)行量化，而數(shù)字PWM調(diào)制是對(duì)信號(hào)在時(shí)域上做量化,，因此必須將時(shí)域上的量化和信號(hào)幅值相關(guān)聯(lián)，即受幅值的調(diào)制,，從而使輸出包含基帶的信息,。一個(gè)n位的PCM碼，是通過(guò)對(duì)一個(gè)采樣周期內(nèi)的采樣值經(jīng)過(guò)2n級(jí)量化編碼得到的,。如果讓轉(zhuǎn)換后的脈寬信號(hào)保持信號(hào)的精度,，則在一個(gè)采樣周期內(nèi)對(duì)一個(gè)采樣值在時(shí)域上也要做2n級(jí)量化。而加入了Σ-Δ調(diào)制器后,，它將再次量化輸入的PCM信號(hào),，將輸入的高精度信號(hào)量化為低精度信號(hào)，而且仍然保持了信號(hào)的信噪比指標(biāo),。量化位數(shù)的降低大大降低了數(shù)字脈寬fs·2n(fs為信號(hào)采樣率),，如果n減小一半,，工作時(shí)鐘將成指數(shù)下降。因此Σ-Δ調(diào)制器的設(shè)計(jì)尤為重要,?？紤]到后級(jí)功率轉(zhuǎn)換器的效率和線性度及系統(tǒng)的功耗，而且調(diào)制器的過(guò)采樣率不會(huì)很高[2],，在設(shè)計(jì)系統(tǒng)時(shí),，將使用多位高階級(jí)聯(lián)的Σ-Δ調(diào)制器，以提高輸入信號(hào)的帶寬,。

　　一般來(lái)說(shuō),，高階Σ-Δ調(diào)制器比低階Σ-Δ調(diào)制器具有更好的性能。但大于二階的不能用線性模型描述,，因?yàn)楸容^器的平均增益減小,，使系統(tǒng)的穩(wěn)定性下降。多級(jí)噪聲模型是解決穩(wěn)定性較好的方案,。該技術(shù)采用了多個(gè)級(jí)聯(lián),、穩(wěn)定的一階回路，每階回路對(duì)上一級(jí)的積分器輸出與數(shù)模轉(zhuǎn)換器（DAC）輸出之差（量化噪聲）進(jìn)行量化,，最后差分求和輸出,，它能夠使量化噪聲得到很好的抑制。多位結(jié)構(gòu)的Σ-Δ調(diào)制器則可提高轉(zhuǎn)換速率和精度,。對(duì)于一個(gè)給定的過(guò)采樣比和濾波器的階數(shù),，這種結(jié)構(gòu)可以提供更大的動(dòng)態(tài)范圍。多位調(diào)制器每增加1位,，信噪比就能增加6dB,，而且它還可以減少帶外的噪聲水平，降低對(duì)后級(jí)模擬濾波器的要求,。但多位調(diào)制器的一個(gè)主要缺點(diǎn)是：由于在多位DAC中的元素不匹配而造成的積分非線性化問(wèn)題,，使每級(jí)的非線性化誤差得不到消除而逐漸累加而造成輸出結(jié)果惡化。本文提出了一種方法：在傳統(tǒng)的MASH結(jié)構(gòu)基礎(chǔ)上,，每級(jí)之間加一條反饋回路[3],。該方法能有效地消除多位DAC非線性化而帶來(lái)的誤差。
1  調(diào)制器原理
　　L階Σ-Δ調(diào)制器如圖2所示,。Σ-Δ調(diào)制器的階數(shù)就是調(diào)制器前向通道積分器的個(gè)數(shù),。從圖中可以看出，L階Σ-Δ調(diào)制器的前向通道包括L個(gè)積分器和嵌于反饋回路的量化器,，每個(gè)積分器的輸入均為前一個(gè)積分器的輸出與1位DAC的輸出之差,。反饋回路的作用使得第一級(jí)積分器的凈輸入趨于零，即DAC的輸出與調(diào)制器的輸入信號(hào)X(n)基本相等,，亦即X(n)≈Y(n),。

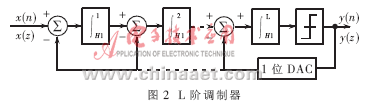
　　由于量化器為非線性元件,，為了分析它所引入的量化誤差，需將量化器近似等效成一個(gè)相加性的白噪聲源e(n),，因此根據(jù)線性化系統(tǒng)疊加原理,，得到調(diào)制器對(duì)信號(hào)和噪聲的傳輸函數(shù)如下：

　　從以上公式可以看出，增加階數(shù),、位數(shù)和過(guò)采樣率都可以讓調(diào)制器的信噪比和動(dòng)態(tài)范圍有不同程度的提高,。但隨著它們的提高，也會(huì)帶來(lái)負(fù)面影響,。在過(guò)采樣率一定的情況下,，增加位數(shù)能夠彌補(bǔ)階數(shù)變高而引起的動(dòng)態(tài)范圍減小的問(wèn)題，信噪比也會(huì)提高,，但它引入的非線性誤差卻會(huì)使結(jié)果惡化,。在減小多位系統(tǒng)中的DAC非線性化問(wèn)題方面，人們提出了很多解決辦法,，包括引入新的結(jié)構(gòu),、校準(zhǔn)技術(shù)、動(dòng)態(tài)元素匹配技術(shù)（DEM）,、雙端量化結(jié)構(gòu)等[4],。在上述的方法中，動(dòng)態(tài)元素匹配技術(shù)在解決多位系統(tǒng)中的非線性化問(wèn)題中是應(yīng)用最廣的,。它通過(guò)計(jì)算出不匹配單元造成的誤差,，從而得到一個(gè)修正算法，通常用得較多的算法有元素隨機(jī)化和元素旋轉(zhuǎn)等,。但DEM的缺陷是強(qiáng)烈依靠它所使用的算法,。例如DEM廣泛使用的DWA數(shù)據(jù)權(quán)重平均算法雖然能夠?qū)Φ谝浑A的噪聲進(jìn)行整形，但是它也引入了信號(hào)依賴誤差而降低了動(dòng)態(tài)范圍,，雖然改進(jìn)的雙向DWA算法能夠降低信號(hào)依賴誤差,，但是使帶內(nèi)的噪聲同時(shí)也增加了。因此,，DEM大體上只是用在一階噪聲整形上[5],。為此本文提出了一種沒(méi)有采用DEM的4階級(jí)聯(lián)調(diào)制器的新方案，它在解決非線性化的問(wèn)題上取得了較好的效果,。
2  調(diào)制器結(jié)構(gòu)
　　本文中沿用了參考文獻(xiàn)[3]的思想，將它的方案用在如圖3所示的更高階的系統(tǒng)中,。在傳統(tǒng)的2-1-1 MASH級(jí)聯(lián)調(diào)制器的基礎(chǔ)上,，除了第一級(jí)外，其余的每級(jí)上都有一個(gè)額外的DAC反饋回路接到上一級(jí)的積分器輸出端來(lái)使DAC的非線性誤差減小,。傳統(tǒng)2-1-1 MASH Σ-Δ調(diào)制器的輸出如下：

　　可以看出最后一級(jí)的DAC誤差ed3已經(jīng)被消除掉了,，ed2的整形函數(shù)也比傳統(tǒng)的調(diào)制器提高了一階,，只有ed1沒(méi)有得到整形，但它相對(duì)于傳統(tǒng)的結(jié)構(gòu)在消除DAC非線性量化誤差方面已經(jīng)有了明顯的提高,。
　　每級(jí)AD/DA轉(zhuǎn)換器位數(shù)的選取取決于結(jié)果所需要的精度與DAC非線性誤差之和的折衷,。顯然每級(jí)只有1位的系統(tǒng)可以完全避免非線性化問(wèn)題，但是最后的精度可能不夠,；相反,，多位系統(tǒng)的精度雖然達(dá)到了，但必須重新審視非線性化問(wèn)題,。因此一個(gè)比較好的折衷辦法就是使用1位和多位的混合系統(tǒng),，系統(tǒng)的第一級(jí)為1位，而其余的為多位,，這樣不僅能夠消除ed1,，還可以使ed2足夠低。
　　當(dāng)輸入信號(hào)很大時(shí),，為了防止過(guò)載,，還必須縮放積分器的增益。增益系數(shù)是每級(jí)積分器的最大線性化輸出范圍和整個(gè)調(diào)制器信噪比的折衷,。設(shè)定每個(gè)積分器的增益系數(shù)為a,、b、c,、d,，利用上面的結(jié)論，若在開始的2階調(diào)制器中使用1位AD/DA轉(zhuǎn)換器,，就可消除ed1,。調(diào)制器的輸出為Y=abcd·z^-4X+(1-z^-1)4E₃+d·z^-1(1-z^-1)3E_d2。
3  仿真結(jié)果
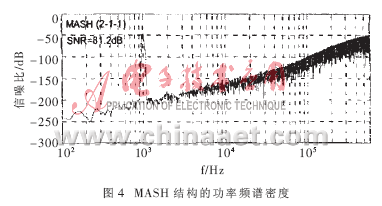
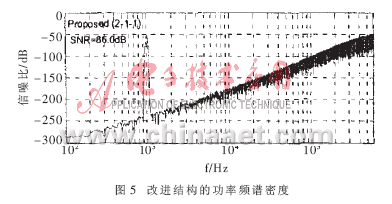
　　利用MATLAB對(duì)本文提出的改進(jìn)結(jié)構(gòu)和傳統(tǒng)的2-1-1結(jié)構(gòu)(MASH結(jié)構(gòu))同時(shí)進(jìn)行了行為仿真和比較,。在本文提出的結(jié)構(gòu)中,，選擇積分器的增益系數(shù)分別為：a=1/2、b=2/5,、c=1/2,、d=1，它的第二級(jí)和第三級(jí)中AD/DA轉(zhuǎn)換器的位數(shù)都為4,，且AD/DA轉(zhuǎn)換器的性能指標(biāo)和MASH結(jié)構(gòu)都一樣,。而在4階MASH結(jié)構(gòu)中，增益系數(shù)分別為：a=1/2,、b=2/5,、c=1、d=1。為了比較非線性化對(duì)2個(gè)調(diào)制器的影響,，假定組成單元的最大不匹配值為0.1%,，積分器最大非線性化范圍為±0.05LSB，設(shè)輸入信號(hào)頻率為1kHz,，信噪比為-20dB,，過(guò)采樣率為32，帶寬為20kHz,，則可得出如圖4和圖5所示的2個(gè)調(diào)制器的功率頻譜密度,。圖 4表明MASH結(jié)構(gòu)中很小的DAC非線性誤差就很容易造成帶內(nèi)干擾。而圖5所示的調(diào)制器盡管信噪比的峰值由于增益系數(shù)比較小而比MASH結(jié)構(gòu)小,，但其信噪比比MASH的要高,。分析它們的信噪比還可以看出，由于DAC的非線性誤差,，MASH結(jié)構(gòu)的信噪比下降了18~20dB,，而本文給出的結(jié)構(gòu)只下降了3~4dB。二者之間15dB的差異充分表明了本文給出的結(jié)構(gòu)在消除DAC非線性誤差方面比傳統(tǒng)的2-1-1級(jí)聯(lián)調(diào)制器要好得多,。

4  結(jié)  論
　　本文分析了Σ-Δ調(diào)制器在數(shù)字音頻中的應(yīng)用,，著重介紹了Σ-Δ調(diào)制器的一個(gè)改進(jìn)方案。實(shí)驗(yàn)結(jié)果表明,，本文提出的多位級(jí)聯(lián)Σ-Δ調(diào)制器能很好地避免DAC的非線性化問(wèn)題,，多位DAC中最后一級(jí)的誤差可以完全消除，而且它前面一級(jí)的誤差也可以得到整形,。仿真結(jié)果表明它的信噪比比傳統(tǒng)的2-1-1級(jí)聯(lián)調(diào)制器要好得多,。
參考文獻(xiàn)
1   Sandler M.Digital Amplification for Consumer Audio，Consumer Electronics[R].2000 ICCE.2000 Digest of Technical  Papers.International Conference on,，2000
2   Sherman J D.Class D Amplifiers Provide High Efficiency   for Audio System[N].EDN Magazine,，1995
3   Fang L，Chao K S.A Multi-bit Σ-Δ Modulator with DAC Error Cancellation[R].In：IEEE Proc 1999 International Symposium on Intelligent Signal Processing and Communication Systems,，1999
4   Kinyua M K,，Chao K S.High Resolution Multi-bit Sigmadelta Modulator Architecture[J/OL].In：IEEE Proc.40th Midwest Symposium on Circuits and Systems，1997
5   Baird R,，F(xiàn)iez T.Linearity Enhancement of Multi-bit  Delta-Sigma A/D and D/A Converters using Data Weighted  Averaging[J].IEEE Trans on Circuits Syst sec,，1995；(42)