摘  要： 為了提高神經網絡進行函數(shù)擬合的精度,，首先在三層徑向基神經網絡基礎上通過增加網絡層次和改變激勵函數(shù)提出了一種四層徑向基小波神經網絡，并采用遺傳算法來確定初始網絡參數(shù),；其次針對遺傳算法中容易早熟的缺點,，在遺傳算法中引入動態(tài)平衡策略，根據(jù)適應度的變化來動態(tài)改變遺傳算法中交叉和變異概率,，從而增加算法全局探索和局部開發(fā)的平衡能力,；最后通過對函數(shù)擬合試驗并與其他方法相比較表明了算法的有效性。
關鍵詞： 徑向基神經網絡,；小波神經網絡,；遺傳算法,；動態(tài)平衡；函數(shù)擬合

1.2 四層徑向基小波神經網絡數(shù)學模型
    (1)網絡輸入第p個樣本對第1層第i個神經元的輸入為：
    

2 利用改進遺傳算法優(yōu)化四層徑向基小波神經網絡
2.1 算法流程
    利用改進遺傳算法優(yōu)化四層徑向基小波神經網絡,，算法流程如圖2所示,。

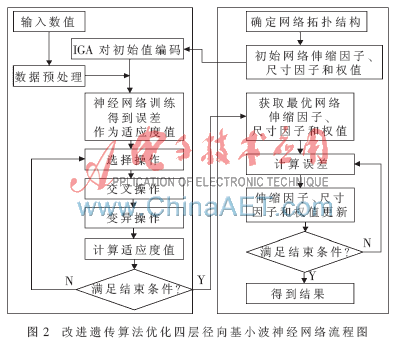
2.2 算法的改進
    遺傳算法是一種應用很廣泛的進化算法，同時其又存在很多難以解決的實際問題,，包括早熟收斂和各個算子概率的選擇以及進化后期搜索效率低,。這些問題導致遺傳算法把握總體的能力較強，但局部搜索能力較差,，最終結果往往不是全局最優(yōu)解[5-6],。因此,，對遺傳算法的研究主要是避免早熟收斂和提高進化后期效率,。總的來看改進方法有改進遺傳操作,、調整遺傳參數(shù)和采用混合遺傳方法等幾種,。
    交叉算子和變異算子決定了遺傳算法的收斂性。交叉算子提供了全局搜索能力,，而變異算子則提供了局部搜索能力[7],。在種群進化初期，應在種群內大范圍地搜索,，進行全局進化從而避免早熟收斂,；到了進化后期，種群成熟度較高,，個體更加逼近最優(yōu)解,，種群應該在局部范圍內搜索，重點進化,，盡可能提高精度,。由此可知，交叉概率和變異概率的選擇很困難,，具有很大的盲目性,，要么根據(jù)遺傳算法理論中各參數(shù)的大致范圍來確定，或者根據(jù)開發(fā)者的經驗來決定[8-9],。這樣的選擇方法經常會導致算法陷入局部最優(yōu),，出現(xiàn)早熟現(xiàn)象。
    動態(tài)平衡策略是一種平衡全局探索能力和局部進化能力的方法,。在基于動態(tài)平衡策略的遺傳算法中,，首先以較大的交叉概率pc1和較小的變異概率pm1進行全局搜索，一旦發(fā)現(xiàn)一個較好的解,，則改變?yōu)橐暂^大的變異概率pm2和較小的交叉概率pc2進行局部搜索,，如果在搜索過程中最優(yōu)解得不到改善,，則再以較大的交叉概率pc1和較小的變異概率pm1進行全局搜索。
    全局搜索主要依靠交叉算子來產生新個體,。隨著種群的不斷進化,，種群越來越成熟，個體的相似性越來越高,，交叉操作很難產生新的個體,，這將影響算法對新的解空間進行搜索，從而導致種群喪失多樣性,，這時應加強個體的變異,。因此，交叉概率應隨著進化過程逐漸變小,，最后趨于某一穩(wěn)定值,，防止算法不能收斂或收斂過程加長；同時變異概率應當越來越大,，以避免個體出現(xiàn)未成熟收斂[10-11],。
    根據(jù)上述策略，pc1和pm1將隨著進化代數(shù)動態(tài)改變：
    
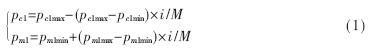
式中,，i為進化代數(shù),，M為總進化代數(shù)，pc1max,、pc1min分別為最大最小交叉概率,，pm1max、pm1min分別為最大最小變異概率,。
    根據(jù)適應度的變化來改變交叉和變異概率,，也就是進行全局搜索和局部優(yōu)化的切換。假設以最大化適應度為目標,，歷代最好適應度為gbest,，當代最好適應度為fbest，以兩者的比值g=fbest/gbest來改變交叉和變異概率,，如果g>k,，則進行局部優(yōu)化，優(yōu)化代數(shù)為num代,，交叉概率和變異概率分別取為pc1,、pm1；如果g<k,，且局部優(yōu)化num代未完成,，交叉概率和變異概率分別取為pc2、pm2,，否則按式（1）更新交叉和變異概率,。其中k∈[0,，1]為系數(shù)。
3 算法有效性驗證
    為了驗證改進算法的性能,，本文選擇函數(shù)擬合進行仿真實驗,，并將實驗結果與其他優(yōu)化方法的計算結果進行比較。為了方便描述,，本文算法簡寫為IGWRN算法,，選取參考文獻[11]中提出的經遺傳算法優(yōu)化的BP神經網絡（簡稱為GABP算法）與參考文獻[12]中提出的三層徑向基小波神經網絡算法（簡稱為WRBF算法）作比較，假定函數(shù)為：
    
  

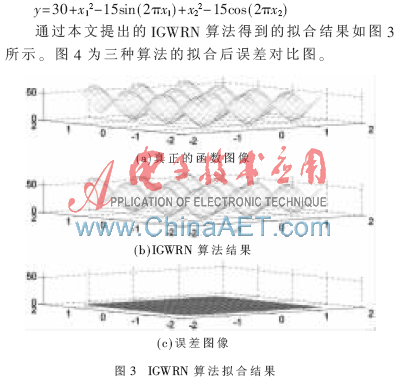
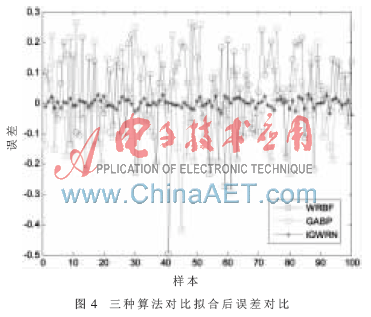
    從圖3和圖4可以看出,，本文提出的IGWRN算法相對于GABP和WRBF算法在擬合精度上有了較大提高,。IGWRN算法運行過程中，其迭代次數(shù)與GABP相比有所增加,，主要原因是IGWRN算法在發(fā)現(xiàn)較好解之后要進行局部搜索,，由此降低了交叉概率，從而使得種群中產生較好新個體的可能性變小,，特別是在進化早期,，對算法的影響更大,。
參考文獻
[1] 褚衍賀,，陳洪建，商艷蘭.RBF神經網絡在變速箱齒輪故障診斷中的應用[J].微型機與應用,，2010,，29(17)：94-97.
[2] 楊超，王志偉.經GA優(yōu)化的WNN在交通流預測中的應用[J].計算機工程,，2011,，37(14)：149-151.
[3] BUHMANN M D.Radial basis functions on compact support[C].Proceedings of the Edinburgh Mathematical Society，1998：33-46.
[4] SHAHIDEHPOUR M,，YAMIN H,，Li Zuyi.Market operations in electric power systems[M].John Wiley&Sons，Inc.,，2002：69-76.
[5] 董福貴,，張世英，譚忠富,，等.基于遺傳算法的小波神經網絡在電價預測中的應用[J].計算機工程,，2005，31(4)：32-33.
[6] SZU H,，CAULFIELD H J.Special section on wavelet  transforms[J].Opt Eng,，1992，31(9)：1823-1916.
[7] 張圓圓,，景曉軍.基于快速遺傳算法的指紋匹配[J].計算機工程,，2011,，37(24)：13-15.
[8] 斯蕓蕓，徐道連,，周卓然.基于遺傳算法和小波神經網絡的語音識別研究[J].微型機與應用,，2011，30(16)：68-71.
[9] 任遠,，白廣忱.徑向基神經網絡在近似建模中的應用研究[J].計算機應用,，2009，29(1)：115-118.
[10] 雷霆,，余鎮(zhèn)危.一種網絡流量預測的小波神經網絡模型[J].計算機應用,，2006，26(3)：526-528.
[11] 馮楠,，王振臣.基于遺傳算法和BP神經網絡的電池容量預測[J].電源技術,，2011，35(12)：1586-1588.
[12] 李偉.基于小波變換和徑向基神經網絡的簽名識別[J].洛陽理工學院學報(自然科學版),，2011,，21(1)：65-68.