摘  要： 針對初始聚類中心對傳統(tǒng)K-means算法的聚類結(jié)果有較大影響的問題,，提出一種依據(jù)樣本點類內(nèi)距離動態(tài)調(diào)整中心點類間距離的初始聚類中心選取方法，由此得到的初始聚類中心點盡可能分散且具代表性,，能有效避免K-means算法陷入局部最優(yōu),。通過UCI數(shù)據(jù)集上的數(shù)據(jù)對改進算法進行實驗，結(jié)果表明改進的算法提高了聚類的準確性,。
關(guān)鍵詞： K-means,；聚類算法；初始聚類中心,；動態(tài)聚類

    聚類分析[1]是基于數(shù)據(jù)集客觀存在著若干個自然類,，每個自然類中的數(shù)據(jù)的某些屬性都具有較強的相似性而建立的一種數(shù)據(jù)描述方法。因而可以講,，聚類分析是將給定的一些模式分成若干組,，對于多選定的屬性或者特征，每組內(nèi)的各樣本模式是相似的,，而與其他組的樣本模式差別較大,。聚類分析有許多具體的算法，從算法策略上看,，可以分為如下幾種典型方法：(1)根據(jù)相似性閾值和最小距離原則的簡單聚類方法,；(2)譜系聚類算法；(3)近鄰函數(shù)法,；(4)動態(tài)聚類法,。其他方法基本是由這四種派生而來。
    在眾多的聚類方法中,，動態(tài)聚類法中的K-means算法因其方法簡單,、效率高、結(jié)果尚令人滿意,，因此得到了廣泛的應(yīng)用,。但是K-means算法本身存在缺陷和不足，如K值的選取,、初始聚類中心的選取以及對噪聲敏感等問題,。學術(shù)界對初始聚類中心的選取提出了多種改進算法，如參考文獻[2]提出利用數(shù)據(jù)樣本的近鄰點信息確定初始聚類中心的方法；參考文獻[3]采用基于密度的思想,，將不重復的核心點作為初始聚類中心,；參考文獻[4]選擇包含數(shù)據(jù)樣本最多的K個類中心作為初始聚類中心；黃韜等[5]通過對數(shù)據(jù)集的多次采樣,，選取最終較優(yōu)的初始聚類中心,。這些算法提高了聚類準確性，但初始中心點的選取未能同時兼顧代表性和分散性的特性,。
    針對樣本點之間的近類內(nèi),、遠類間的分布特性，本文提出一種依據(jù)類內(nèi)距離動態(tài)調(diào)整中心點類間距離的初始聚類中心選取方法,，得到的初始聚類中心能盡量分散,，很好地代表K個簇，并且,，掃描一遍數(shù)據(jù)集即可完成初始聚類中心的選取,。實驗表明，與隨機選取初始聚類中心的傳統(tǒng)K-means算法相比,，該方法提高了聚類的準確率,，使得聚類結(jié)果更穩(wěn)定。
1 K-means算法的基本理論
    K-means算法有兩個階段,，第一個階段是確定K個中心點,，每一類有一個中心點；第二個階段是把數(shù)據(jù)集的每個樣本點關(guān)聯(lián)到最近的中心點,，并由此循環(huán)得到新的K個中心點,。循環(huán)的結(jié)果就是中心點位置不斷地變動，直到穩(wěn)定不變,，標志著聚類收斂,。
    設(shè)待分類的數(shù)據(jù)集為{x1，x2,，…,，xC}，聚類的個數(shù)為K,。算法的具體步驟如下：

    在K-means算法中,，數(shù)據(jù)之間的相似度用歐氏距離來衡量，距離越大越不相似,，距離越小越相似,，兩個簇之間數(shù)據(jù)太密集就會合并為新的聚類簇，而離兩個聚類簇稀疏的數(shù)據(jù)就會形成新的簇,。因此如果選取兩個簇密集區(qū)域的聚類中心的平均值和離簇稀疏的數(shù)據(jù)作為初始聚類中心,，將有利于目標函數(shù)的收斂,。
    由此，本文將依據(jù)樣本點實際分布情況,，利用類內(nèi)最短距離調(diào)整中心點的類間距離,，不斷更新優(yōu)化初始聚類中心?；舅悸啡缦拢?1)隨機選取的K個樣本（記為集合L）作為初始中心點,，按式（4）計算這K個數(shù)據(jù)兩兩之間的最小距離作為初始類間距離limit，設(shè)集合R=U-L,；(2)按式(4)計算R中任一樣本點到L的最短距離t=Dist[ri,，L](ri表示R中第i個樣本點)，如果t大于limit,，則刪除集合L中最近的兩個點,，把這兩點的中點ri加入到集合L中，更新limit為t,。否則,，不做任何操作,；(3)更新R=R-ri,，重復步驟(2)，直至R為空,。
    假設(shè)現(xiàn)在有一個二維數(shù)據(jù)樣本集合,，含有6個樣本點，分成3個聚類簇,，如圖1所示,。

    按照本文的算法思想：(1)首先隨機選取3個初始點A、C,、D構(gòu)成集合L,，按式(4)計算這3個數(shù)據(jù)兩兩之間的最小距離作為初始閾值limit，設(shè)集合R=U-L={B,、E,、F}；(2)按式(4)計算R中任一樣本點到L的最短距離t=Dist[B,，L],，若t大于閾值limit，則刪除集合L中最近的兩個點C和D,，并把這兩點的平均值和B加入到集合L中,，更新閾值limit為Dist[B，L],；(3)更新R=R-B={E,、F}。重復步驟(2)，直到R為空,。最終得到的聚類中心接近于聚類算法期望得到的聚類中心,。
    由上述動態(tài)選取初始聚類中心算法得到的聚類中心作為K-means算法的初始聚類中心，即為改進的動態(tài)K-means算法,。
    改進的動態(tài)K-means算法的時間復雜度主要由兩部分組成,，一部分是生成初始聚類中心的時間，另一部分是迭代所需要的時間,。改進的動態(tài)K-means算法計算出初始聚類中心需要的時間復雜度為O(K×C×N),，其中K為聚類數(shù)，C為所有樣本數(shù)據(jù)的個數(shù),，N為樣本屬性,。
3 實驗與結(jié)果分析
    為驗證改進算法的有效性，本文采用UCI標準數(shù)據(jù)集中的葡萄酒Wine數(shù)據(jù)集和鳶尾花Iris數(shù)據(jù)集,。對各數(shù)據(jù)集的描述如表1所示,。

    對于表1所描述的數(shù)據(jù)，本文做對比實驗,，比較隨機選取聚類中心的K-means算法和本文改進的動態(tài)K-means算法,，分別在Wine和Iris數(shù)據(jù)集上進行10次試驗。本文用隨機的方式選取初始中心點,，實驗結(jié)果如表2,、表3、圖2和圖3所示,。

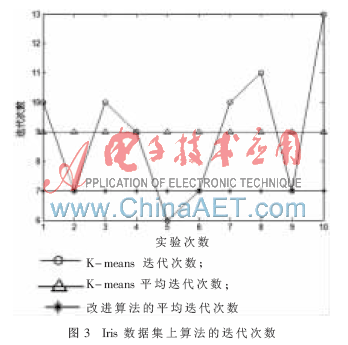
    從表2和圖2可以看出,，在Wine數(shù)據(jù)集進行10次實驗，K-means算法的準確率在53.37%~70.22%之間浮動,，平均準確率為62.25%,；迭代次數(shù)最少5次，最多16次,，平均迭代次數(shù)為9,。由此可見，K-means聚類算法結(jié)果不穩(wěn)定,，并且受初始中心點影響很大,。本文算法平均準確率為70.34%，平均迭代次數(shù)為5,。從表3和圖3可以看出,，在Iris數(shù)據(jù)集進行10次實驗，K-means算法平均準確率為75%,，平均迭代次數(shù)為9次,，本文算法平均準確率為89.47%,，平均迭代次數(shù)為7次。實驗結(jié)果表明,，本文改進的動態(tài)K-means算法選取的初始聚類接近簇中心,，收斂速度快，準確率高,，聚類效果好,。
    K-means算法的聚類結(jié)果受初始聚類中心影響很大且迭代次數(shù)多，本文改進的算法優(yōu)化了初始聚類中心,，有效地提高了收斂速度,，提高了聚類的準確率。但本文方法受噪聲點影響較大,，下一步將對減少噪聲點的影響方面進行學習和研究,。
參考文獻
[1] 孫即祥，姚偉,，騰書華.模式識別[M].北京：國防工業(yè)出版社,，2009.
[2] CAO F Y，LIANG J Y,，JIANG G．An initialization method for the K-means algorithm using neighborhood model[J]．Computers＆Mathematics with Applications,，2009，58(3)：474－483．
[3] 張琳,，陳燕,，汲業(yè),，等.一種基于密度的K-means算法研究[J].計算機應(yīng)用研究,，2011，28(11)：4071-4073.
[4] 張瓊,，張瑩,，白清源，等.基于Leader的K均值改進算法[J].福州大學學報,，2008,，36(4)：493-496.
[5] 黃韜，劉勝輝,，譚艷娜.基于K-means聚類算法的研究[J].計算機技術(shù)與發(fā)展,，2011，21(7)：54-57.