FIR濾波器具有幅度特性可隨意設計,、線性相位特性可嚴格精確保證等優(yōu)點，因此在要求相位線性信道的現代電子系統(tǒng),，如圖像處理,、數據傳輸等波形傳遞系統(tǒng)中，具有很大吸引力,。本文簡單介紹了其線性相位條件和設計方法,，并且提供了一種用DSP實現的方法。
　　關鍵詞：IIR（Infinite Impulse Response）　FIR（Finite Impulse Response）　DSP（Digital Signal Processor）

一,、 引　言

　　在許多信息處理過程中,，如對信號的過濾、檢測,、預測等,，都要廣泛地用到濾波器，而數字濾波器則因其設計靈活,、實現方便等特點而廣為接受,。
　　所謂數字濾波器就是具有某種選擇性的器件、網絡或以計算機硬件支持的計算程序,。其功能本質是按事先設計好的程序,，將一組輸入的數字序列通過一定的運算后轉變?yōu)榱硪唤M輸出的數字序列，從而改變信號的形式和內容,，達到對信號加工或濾波以符合技術指標的要求,。

二,、 數字濾波器的兩種類型

　　對于一般的數字濾波器，按照單位沖激響應可分為無限長沖激響應IIR（Infinite Impulse Response）系統(tǒng)和有限長沖激響應FIR（Finite Impulse Response）系統(tǒng),。
　　在IIR系統(tǒng)中,，用有理分式表示的系統(tǒng)函數來逼近所需要的頻率響應，即其單位沖激響應h(n)是無限長的,；而在FIR系統(tǒng)中,，則用一個有理多項式表示的系統(tǒng)函數去逼近所需要的頻率響應，即其單位沖激響應h(n)在有限個n值處不為零,。
　　IIR濾波器由于吸收了模擬濾波器的結果,，有大量的圖表可查，可以方便,、簡單,、有效地完成設計，效果很好,，但是其相位特性不好控制,，必須用全通網絡進行復雜的相位較正，才能實現線性相位特性的要求,。
　　FIR濾波器則可在幅度特性隨意設計的同時，保證精確,、嚴格的線性相位特性,。這在要求相位線性信道的現代電子系統(tǒng)，如圖像處理,、數據傳輸等波形傳遞系統(tǒng)中,，是具有很大吸引力的。而且,，其單位沖激響應是有限長的,，不存在不穩(wěn)定的因素，并且可用因果系統(tǒng)來實現,。
　　下面著重討論具有線性相位特性的FIR濾波器,。

三、 FIR濾波器線性相位特性的條件及設計方法

　　1.線性相位條件
　　為保證濾波器帶內輸出信號的形狀保持不變,，常常要求濾波器單位沖激響應h(n)的頻率響應H(ejω)應具有線性的相頻特性,，即H(ejω)=H(ω)e-jωk，其中H(ω)為幅頻特性,，k為正整數,。由傅氏變換的特性可知，線性相位濾波器只是將信號在時域上延遲了k個采樣點,，因此不會改變輸入信號的形狀,。
　　可以證明,，如果濾波器單位沖激響應h(n)為實數，且滿足：偶對稱即h(n)=h(N-1-n)或奇對稱h(n)=-h(N-1-n)時,，則其相頻特性一定是線性的,。
　　2.設計方法
　　(1) 窗函數設計法
　　從時域出發(fā)，把理想的無限長的hd(n)用一定形狀的窗函數截取成有限長的h(n),，以此h(n)來逼近hd(n),，從而使所得到的頻率響應H(ejω)與所要求的理想頻率響應Hd(ejω)相接近。優(yōu)點是簡單,、實用,，缺點是截止頻率不易控制。
　　(2) 頻率抽樣設計法
　　從頻域出發(fā),，把給定的理想頻率響應Hd(ejω)加以等間隔抽樣,，所得到的H(k)作逆離散傅氏變換，從而求得h(n) ,，并用與之相對應的頻率響應H(ejω)去逼近理想頻率響應Hd(ejω),。優(yōu)點是直接在頻域進行設計，便于優(yōu)化,，缺點是截止頻率不能自由取值,。
　　(3) 等波紋逼近計算機輔助設計法
　　前面兩種方法雖然在頻率取樣點上的誤差非常小，但在非取樣點處的誤差沿頻率軸不是均勻分布的,，而且截止頻率的選擇還受到了不必要的限制,。因此又由切比雪夫理論提出了等波紋逼近計算機輔助設計法。它不但能準確地指定通帶和阻帶的邊緣,，而且還在一定意義上實現對所期望的頻率響應實行最佳逼近,。

四、 FIR濾波器的實現

　　不論是窗函數設計法,，還是頻率抽樣設計法,，都要求出濾波器的單位沖激響應h(n)，然后才能在時域中實現頻域中的濾波,。
　　1.濾波系統(tǒng)的差分方程
　　在頻域,，當其輸入信號為X(ejω)時，如濾波器的頻率響應為H(ejω),，則其輸出信號為Y(ejω)=X(ejω)H(ejω),。
　　在時域，設濾波器的單位沖激響應h(n)為一N點序列,，即0≤n≤N-1時h(n)的值不為零,，根據離散傅氏變換的性質，則可以將濾波器的輸入序列x（n）的響應y（n）表示為x（n）與h(n)的卷積和,，即：

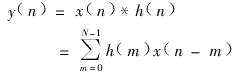
　　這就是濾波系統(tǒng)的差分方程,，它給濾波器的實現奠定了理論基礎,。即求出時域的h(n)后，便可通過卷積來實現頻域的濾波,。
　　2.卷積和運算的實現
　　(1) h(n)序列N個點數值的存儲
　　由于h(n)是根據濾波性能要求已經設計好的有限長單位沖激響應,，故其N個點的數值是已知的，因此可以存放在ROM或RAM當中,，且對應著N個不同的地址,，便于尋址。
　　(2) 輸入序列x（n）的移位寄存
　　輸入序列x（n）是不斷變化的,，因此只能對其進行移位寄存,，寄存器的個數為N，即N個寄存器中分別存放著x（n）,、x（n-1）……x（n-N+1）,，它們都隨著n的變化而變化。
　　(3) 乘法器
　　用以完成兩個數值的乘法,，即h(m)x（n-m）,，也就是將存儲器中N地址所對應的N個固定數值h(m)分別與N個移位寄存器中的不斷變化的N個變化數值x（n-m）相乘。
　　(4) 累加器
　　用以實現N個乘積的累加,，即將當前x（n）所對應的N個乘積進行累加,，所得到的和就是y（n）。當濾波器的下一個輸入值即x（n +1）到來時,，累加器清零,，并重新將下一組x（n +1）所對應的N個乘積進行累加，所得到的和就是y（n +1）,。
　　3.DSP的支持
　　DSP作為信號處理應用,，與一般微處理器有很大的區(qū)別,。
　　(1) 哈佛結構：采用多個并行存儲器塊結構,，使得能夠訪問的存儲器個數增加，從而減少在一個指令周期中所需存儲器操作周期數,。
　　(2) 乘加流水線為核心的數據通路：卷積和運算的基本操作就是乘法與加法,，DSP則將相乘及累加統(tǒng)一考慮，構成以乘法器,、加法器流水線為中心的運算部件,。
　　(3) 特殊的指令：指令RPT由數據存儲器指定重復次數，指令MACD可以一次完成相乘并帶數據移位的累加,，因此使得每一級FIR濾波器只需一個指令周期,。
　　(4) 指令系統(tǒng)的多級流水線：采用多級流水線操作方式，可以把指令周期減小到最小值,，同時也就增加了數字信號處理器的吞吐量,。

五,、 具體電路框圖及程序流程圖

　　圖 1為FIR濾波器DSP實現的電路方框圖，其核心部分為TI公司生產的DSP芯片TMS320C203 ,，EP2ROM和RAM是其外圍電路,。DSP送給A/D抽樣時鐘，對輸入的模擬信號抽樣,，即將模擬信號轉換成數字信號,，然后讀取每一次的抽樣值，并對抽樣值進行卷積運算（FIR數字濾波）,，最后將運算結果（濾波后的數字信號）送至D/A ,，轉換成模擬信號進行輸出。

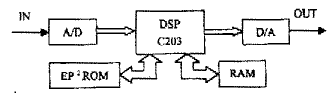
圖 1　電路框圖

　　圖 2為程序流程圖,，說明如下：

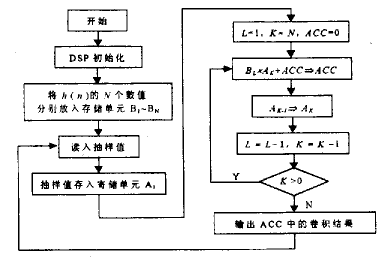
圖 2　程序流程圖

　　(1) 對DSP進行初始化,，定義DSP的一些向量和工作模式；
　　(2) 為數字濾波作準備,，將預先設計好的有N個抽頭的FIR數字濾波器的沖激響應序列h(n)中的N個數值放入存儲單元B1～BN,；
　　(3) 作好濾波準備工作后，開始進行抽樣,，并讀入抽樣值,，放入存儲單元A1中；
　　(4) 之后便對抽樣值進行運算處理：
　　(a) 將累加器清零,，并設置兩個準備相乘的存儲單元A與B的初始值K和L;
　　(b) 將第K個抽樣值AK與沖激響應序列的第L個數值BL相乘（K+L=N+1）,，并將乘積送入累加器進行累加；
　　(c) 將第K-1個抽樣值AK-1放入AK,，此時AK中原數值被覆蓋,；
　　(d) 重復(b)～(c)，直至共完成N次乘加運算,。
　　(5) 輸出處理結果,；
　　(6) 重復(3)～(5)。

六,、 結束語

　　FIR濾波器具有嚴格的線性相位,，且是可物理實現的因果系統(tǒng)，因此被廣泛地應用在現代通信技術當中,，如解調器中的位同步與位定時提取,、自適應均衡去碼間串擾以及話音的自適應編碼等?？梢妼IR濾波器的研究是具有非常重要的現實意義的,。