摘  要： 針對(duì)ZigBee技術(shù)廣泛采用的的三邊測(cè)量定位方法應(yīng)用于二維定位的問(wèn)題,，分析其因各節(jié)點(diǎn)安裝高度不同而產(chǎn)生的誤差,。為維持ZigBee技術(shù)低成本的特點(diǎn)，導(dǎo)出了RSSI值修正條件及RSSI修正值與實(shí)測(cè)值的函數(shù)關(guān)系,。在不增加算法復(fù)雜度的情況下,，對(duì)由錨節(jié)點(diǎn)安裝高度不一致造成的誤差進(jìn)行了抑制，并在CC2431模塊上實(shí)現(xiàn)了改進(jìn)后的定位算法,。結(jié)果表明,，改進(jìn)后的定位算法以較小的系統(tǒng)開(kāi)銷(xiāo)提高了定位精度，具有一定的實(shí)用性和通用性。
關(guān)鍵詞： ZigBee,；三邊測(cè)量,；定位；誤差,；CC2431

　ZigBee技術(shù)以獨(dú)特的低成本,、低功耗、低速率的特點(diǎn),，而擁有其他無(wú)線通信技術(shù)所無(wú)可比擬的優(yōu)勢(shì),。同時(shí)在其成本變化不大的情況下，增加硬件定位引擎,，僅消耗極小的硬件資源,，利用原有網(wǎng)絡(luò)條件就能實(shí)現(xiàn)無(wú)線定位，進(jìn)一步拓展了ZigBee技術(shù)的應(yīng)用,?；诘竭_(dá)時(shí)間（TOA）、到達(dá)時(shí)間差（ODOA）,、到達(dá)角度（AOA）,、接收信號(hào)強(qiáng)度（RSSI）的定位機(jī)制都適用于IEEE802.15.4網(wǎng)絡(luò)[1]。而基于RSSI的定位機(jī)制更符合ZigBee技術(shù)低成本的特點(diǎn),，并能滿足大部分低精確度定位的要求,。
1 三邊測(cè)量定位
1.1 原始定位方法
　圖1是一個(gè)理想的定位場(chǎng)景，節(jié)點(diǎn)1,、2,、3為已知坐標(biāo)的錨節(jié)點(diǎn)，節(jié)點(diǎn)4為需定位的盲節(jié)點(diǎn),。定位方法是將由RSSI值換算而來(lái)的r1、r2,、r3值,，及錨節(jié)點(diǎn)坐標(biāo)代入矩陣式（1），求解盲節(jié)點(diǎn)坐標(biāo)值（x,，y）,。


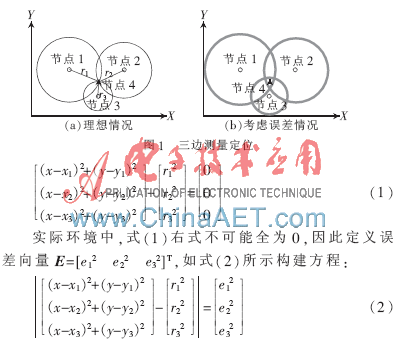
　顯然若使式（1）與式（4）的x、y值同解,，當(dāng)且僅當(dāng)z1=z2=z3=c,。由此利用式（1）進(jìn)行定位計(jì)算時(shí)，若錨節(jié)點(diǎn)安裝高度均與盲節(jié)點(diǎn)高度相等,，則安裝高度不會(huì)產(chǎn)生xy平面上的定位誤差,。但在實(shí)際應(yīng)用中，因現(xiàn)場(chǎng)情況限制,，錨節(jié)點(diǎn)往往安裝位置較高,，而盲節(jié)點(diǎn)手持或安裝于移動(dòng)物體上,，因此錨節(jié)點(diǎn)與盲節(jié)點(diǎn)不可能安裝在同一水平面上。此時(shí),，式（1）,、式（4）有不同解，這將在理論上產(chǎn)生定位誤差,。
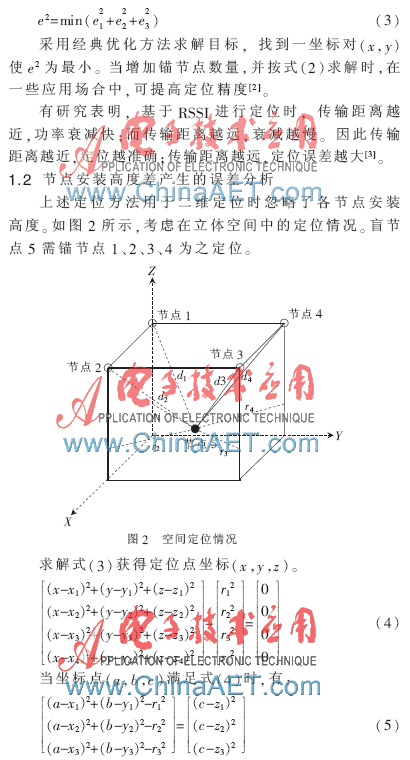
　在一定值場(chǎng)景中,，如圖2中4個(gè)錨節(jié)點(diǎn)安裝高度為3 m，各錨節(jié)點(diǎn)在xy軸的投影點(diǎn)組成一邊長(zhǎng)為8 m的正方形,。x軸和y軸均以2 m的步長(zhǎng)取計(jì)算點(diǎn),，求解式（3）時(shí)，采用有約束非線性規(guī)劃法,，求得錨節(jié)點(diǎn)與盲節(jié)點(diǎn)的高差分別為2 m和3 m時(shí)的理論誤差分布,，如圖3所示。由圖可知,，高差越大,，各點(diǎn)誤差值普遍增大，這對(duì)小空間內(nèi)的定位準(zhǔn)確度造成較大影響,。
1.3 算法改進(jìn)
　前述算法出現(xiàn)誤差的根本原因在于定位計(jì)算時(shí)忽略了高差因素δh,，CC2431的定位引擎輸入?yún)?shù)不包括節(jié)點(diǎn)安裝高度[4]。但考慮到δh對(duì)于二維定位,，如得到各錨節(jié)點(diǎn)到盲節(jié)點(diǎn)的投影距離,，僅需在xy平面上進(jìn)行計(jì)算。根據(jù)式（3）消去z軸的影響因素,。改造式（2）為：

　為減少CC2431在進(jìn)行RSSI值修正時(shí)的系統(tǒng)開(kāi)銷(xiāo),，預(yù)先代入A、n,、δh值等常數(shù)逐點(diǎn)計(jì)算式（8）,，得到修正值。盲節(jié)點(diǎn)進(jìn)行修正值計(jì)算時(shí),，如修正點(diǎn)較少時(shí)可采用查表法計(jì)算,，當(dāng)各錨節(jié)點(diǎn)安裝高度不同或修正點(diǎn)較多時(shí)則采用多項(xiàng)式擬合法計(jì)算。
2 實(shí)驗(yàn)對(duì)比
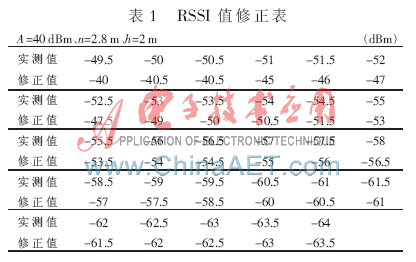
　本實(shí)驗(yàn)場(chǎng)景為長(zhǎng)寬為8 m×8 m,，凈高為3.2 m的室內(nèi)空間,，分別在4個(gè)墻角安裝錨節(jié)點(diǎn)CC2430，安裝高度為2.8 m,。手持盲節(jié)點(diǎn)CC2431距地約0.8 m,。以1 m為步長(zhǎng)，總計(jì)測(cè)量81個(gè)點(diǎn)位接收到4個(gè)RSSI值。由式（7）,、式（8）得到修正表,，見(jiàn)表1。修正表僅占用58 B的存儲(chǔ)空間,，本次實(shí)驗(yàn)采用查表法進(jìn)行修正,。
為對(duì)改進(jìn)前后的效果進(jìn)行比較，每次定點(diǎn)測(cè)量都連續(xù)啟動(dòng)定位引擎兩次,，并分別輸入RSSI（實(shí)測(cè)值）和RSSI（修正值）,，將兩次得到的定位坐標(biāo)送至PC，經(jīng)Matlab處理后,，得到改進(jìn)后與改進(jìn)前誤差的差值表,，如表2所示。

　由表2可見(jiàn),，改進(jìn)算法提高了散布在錨節(jié)點(diǎn)附近位置的定位精度,，對(duì)遠(yuǎn)離錨節(jié)點(diǎn)的位置因不滿足修正條件，則保持了原算法所得到的定位坐標(biāo),。較好地解決了要求傳輸距離盡可能近與近距離時(shí)安裝高差將產(chǎn)生較大誤差之間的矛盾,。

　本文分析了基于ZigBee的三邊測(cè)量定位算法在二維定位上，因節(jié)點(diǎn)安裝高度差產(chǎn)生定位誤差的本質(zhì)原因,，并通過(guò)Matlab實(shí)現(xiàn)了不同高差下理論誤差的對(duì)比,。提出了抑制該誤差的RSSI修正值方法。最后通過(guò)實(shí)測(cè)對(duì)提出的方法進(jìn)行了驗(yàn)證,，體現(xiàn)出RSSI修正值法的有效性,。
參考文獻(xiàn)
[1] 高守瑋，吳燦陽(yáng).ZigBee技術(shù)實(shí)踐教程[M].北京：北京航空航天大學(xué)出版社,，2009.
[2] FARAHANI S. ZigBee wirleless networks and transceivers[M]. USA： Newnes,，2008.
[3] 孫佩剛，趙海,，羅玎玎,，等.智能空間中RSSI定位問(wèn)題研究[J]，電子學(xué)報(bào),，2007，35（7）：1242-1243.
[4] Chipcon Inc.CC2431 Datasheet[S].2006. 5-9.
[5] 王靜,，張會(huì)清.基于ZigBee的無(wú)線網(wǎng)絡(luò)定位技術(shù)的研究與實(shí)現(xiàn)[J],，傳感器與微系統(tǒng)，2010,，29（2）：15-16.