摘  要： 綜述了基于馬爾科夫過程的風電機組檢修策略。首先介紹了馬爾科夫過程及相關理論知識,，并分析其應用于風電機組檢修中的可行性,；然后分別從基于風電機組運行可靠性最優(yōu)策略建立可靠性模型和基于維護成本最優(yōu)策略建立老化模型兩方面入手，指出各自考慮的側重點,，總結了國內外學者基于馬爾科夫過程理論對風電機組檢修策略的研究現(xiàn)狀,；最后指出由單一部件到多部件進行整臺風電機組優(yōu)化檢修和風電場多臺機組聯(lián)合檢修是未來的研究趨勢。
關鍵詞： 風電機組,； 馬爾科夫過程,； 可靠性模型； 老化模型,； 檢修策略

    風能作為一種蘊藏量巨大且無污染的可再生能源,，越來越受到世界各國的關注。風力發(fā)電產業(yè)迅速發(fā)展,，特別是近幾年來,，風電總裝機容量大幅增加。隨著風力發(fā)電行業(yè)的快速增長,，高故障率和高維護成本制約著風電產業(yè)的發(fā)展,因此有必要對風電機組的檢修策略進行研究,。目前風電場主要采取定期檢修方式，這種檢修方式按照固定的周期對設備進行檢修,，沒有考慮到設備實際的運行狀況,，容易造成因檢修不足而導致重大故障的發(fā)生或因檢修過度而導致檢修費用過高等后果。因此研究新的檢修策略來合理地維護風電機組成為行業(yè)研究熱點,。
    風電機組的狀態(tài)轉移是一個隨機過程,。大多數工程現(xiàn)象都可以用隨機過程來描述。1906年,，俄國數學家MARKOV A A最早提出并研究了一種能用數學分析方法研究自然過程的一般圖式——馬爾科夫鏈,，同時開創(chuàng)了對一種無后效性的隨機過程——馬爾科夫過程的研究。
    馬爾科夫過程描述了一種系統(tǒng)的變化情況與以前系統(tǒng)所處的狀態(tài)無關的隨機過程,，是對風電機組運行狀態(tài)建模的有力工具,。目前已有一些國內外學者將馬爾科夫過程理論應用在風力發(fā)電機的檢修中，研究主要集中在：基于馬爾科夫過程建立可靠性模型和基于馬爾科夫鏈建立老化模型,。本文主要從這兩個方面對馬爾科夫過程理論在風力發(fā)電機組檢修策略中的應用現(xiàn)狀進行介紹和評述,，并提出了在今后研究該問題時值得關注的方向。
1 馬爾科夫過程及相關理論
1.1 馬爾科夫過程和馬爾科夫鏈
    已知時刻t系統(tǒng)所處的狀態(tài),，在時刻以后,，系統(tǒng)的變化情況與以前系統(tǒng)所處的狀態(tài)無關的隨機過程稱為馬爾科夫過程。時間和狀態(tài)都是離散的馬爾科夫過程,稱為馬爾科夫鏈[1],。
1.2 馬爾科夫決策過程
    馬爾科夫決策過程MDP(Markov Decision Process)是指決策者周期或連續(xù)地觀察具有馬爾科夫性的隨機動態(tài)系統(tǒng),，序貫地作出決策,。即根據每個時刻觀察到的狀態(tài)，從可用的行動集合中選用一個行動作出決策,，系統(tǒng)下一步隨機地轉移到一個新的狀態(tài),，相應給予決策者一個報酬,。決策者根據新觀察到的狀態(tài)作新的決策,，依此反復地進行[2]。風力發(fā)電機組檢修的目標是成本最優(yōu),，那么利用MDP就是要求出成本最小的策略,。但是考慮到風力發(fā)電機的各個老化狀態(tài)的停留時間服從一定分布，符合半馬爾科夫決策過程的要求,，采用半馬爾科夫決策過程SMDP(Semi-Markov Decision Process)優(yōu)化維修策略更加合理,。
    部分可觀察馬爾科夫過程POMDP(Partially Observable Markov Decision Processes)指決策者不能直接觀察到狀態(tài)，但能利用隨機環(huán)境中部分觀察到的信息進行決策[3],。風力發(fā)電機組部件的狀態(tài)可以通過狀態(tài)監(jiān)測的傳感器所發(fā)出的信號來評估,。描述此信號傳達的信息，就是指定一個關于實際狀態(tài)的概率向量代表對相應的真實狀態(tài)的一個信念,，POMDP問題就可以轉化為基于信念狀態(tài)空間的馬爾科夫鏈來求解,。
2 基于馬爾科夫過程建立風電機組的可靠性模型
     可靠性模型的建立通常是為了對所研究的系統(tǒng)的可靠性進行量化評估，制定適當的維修策略以獲得較高的可用率,。各部件之間的狀態(tài)轉移過程滿足馬爾科夫過程的基本假設,，因此可以基于馬爾科夫過程建立可靠性模型。馬爾科夫過程已經應用在電力系統(tǒng)領域中的一些可靠性研究中[4-7],，下面介紹其用于風力發(fā)電機組相關系統(tǒng)的可靠性建模的方法,。
    參考文獻[8]對風力發(fā)電機組的電氣系統(tǒng)進行拆分，分別建立了感應發(fā)電機,、轉換器,、碳刷和滑環(huán)各子系統(tǒng)的可靠性模型。通過某子系統(tǒng)下的各組件的故障率和修復率,，利用頻率平衡法計算出該子系統(tǒng)的故障率和修復率,，從而建立了基于馬爾科夫過程的風力發(fā)電機組電氣系統(tǒng)的可靠性模型。
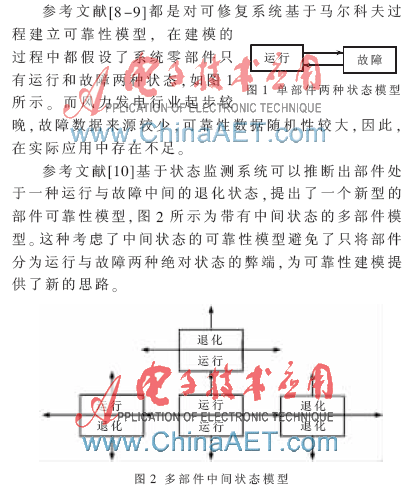
    參考文獻[9]基于參考文獻[8]中可靠性建模的方法,，以雙饋風力發(fā)電機為例,，根據風力發(fā)電機組各子系統(tǒng)之間的功能關系將其拆分為幾個模塊，假設子系統(tǒng)下的各個部件只有正常和故障兩種狀態(tài),，運用馬爾科夫過程數學模型和可靠性理論建立風力發(fā)電機組的可靠性模型,，在此基礎上構造風電機組老化和隨機故障后全面修復的維修模型，從而制定風電機組可靠性最優(yōu)時的維修策略,。

3 基于馬爾科夫鏈建立老化模型
    將風力發(fā)電機的老化過程視為符合馬爾科夫過程的離散的老化狀態(tài),，建立其多階段老化模型。根據具體老化模型，采取合適的馬爾科夫決策過程,，可以達到優(yōu)化檢修成本的目的,。
    參考文獻[11]提出了基于馬爾科夫鏈的多階段老化模型，并考慮了服從泊松分布的隨機故障,，提出了半馬爾科夫過程的優(yōu)化檢修方法,。如圖3所示，F(xiàn)0為該隨機故障,，?姿0為其轉移率,，?姿為兩個老化階段間的轉移率。通過確定設備老化過程中的維修動作和檢測時間間隔,，獲得最小運行維護成本,。最后將該方法應用到風電機組齒輪箱的優(yōu)化檢修中，說明此檢修策略相比傳統(tǒng)定期檢修方法,，可以有效減少平均成本,。

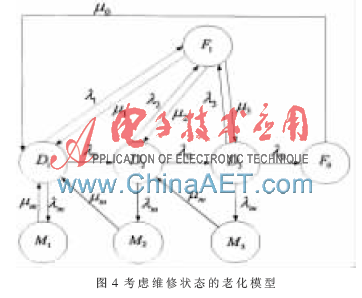
    也有學者將維修狀態(tài)納入到老化模型中[12-13]，參考文獻[9]基于之前提到的可靠性模型計算出整機的故障率和修復率后,，提出了一個整機老化和隨機故障后全面修復的維修模型,如圖4所示,。其中，F(xiàn)1代表偶然故障狀態(tài),，M1,、M2、M3代表預防性維修狀態(tài),，λ1,、λ2、λ3和μ1,、μ2,、μ3分別表示整機系統(tǒng)在各個老化階段內總的失效率和修復率。根據維修模型得到狀態(tài)轉移矩陣,，進而列出各狀態(tài)的穩(wěn)態(tài)方程,，風力發(fā)電機組正常工作的概率最高時為可靠性最高，由此計算出風力發(fā)電機組可靠度最優(yōu)時的預防性維修平均時間間隔,。

    以上的研究主要考慮了機組本身的老化特點,，而在風力發(fā)電機的實際檢修工作中，天氣條件直接影響具體檢修動作的執(zhí)行和備件物流所需的時間,。因此,，有部分學者將其作為影響因子引入到檢修策略分析中。
　參考文獻[14]考慮風速對維修動作的限制,，在檢修時間函數中引入參數來表示風速小于預防性維修和故障后維修的最大允許風速的概率,。將部件老化過程離散成有限的老化狀態(tài),，以長期折扣成本最低為目標，建立基于半馬爾科夫決策過程的狀態(tài)維修優(yōu)化模型,。最后,，以某風力機齒輪箱為例，分別求出在等周期,、非等周期檢測條件下的最優(yōu)檢測時間間隔和維修成本,，并提出在非等周期檢測方式下，總能得到不劣于等周期檢測方式下的維修折扣成本,。
    參考文獻[15]研究在隨機天氣條件下運行的風力機最佳維修策略,?？紤]到天氣條件會限制檢修可行性,，從而造成收入虧損，模型中引入了由于惡劣天氣條件而禁止預防性維修和故障后維修的概率,。通過建立一個多狀態(tài)的,、部分可觀察的馬爾科夫決策過程模型來表示風力發(fā)電機的老化過程和策略優(yōu)化問題。最終得到一組關于最優(yōu)策略的閉式表達式,，由此得出檢修成本最優(yōu)策略區(qū)域圖,。
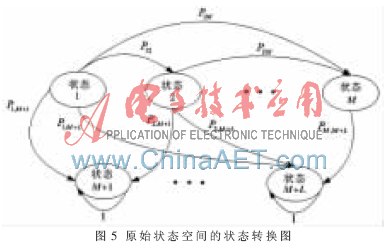
    參考文獻[16]提出了一個考慮季節(jié)交替的動態(tài)狀態(tài)檢修策略，即在不同時期,，對不同的故障模式分別引入參數來表示在該時期的天氣條件下不允許故障檢修和預防性維修的概率,。不同的故障模式，即將隨機故障細化為具體的故障模式,，如該文以齒輪箱為例,，具體故障為軸承故障、齒輪故障,、潤滑油故障等,。圖5為原始狀態(tài)空間的狀態(tài)轉換圖，狀態(tài)1到狀態(tài)M為老化狀態(tài),，狀態(tài)M+1到狀態(tài)M+L為故障狀態(tài),。建立一個部分可觀察馬爾科夫模型來描述該問題，以獲得風力發(fā)電機組的整個壽命期的最小運行與維護成本,。最后以某齒輪箱為例比較了常規(guī)的定期檢修,，不考慮季節(jié)變化影響的靜止狀態(tài)檢修以及該動態(tài)檢修策略的效果，證明動態(tài)檢修策略在降低故障率和運行維護成本上具有明顯優(yōu)勢,。

4 展望與進一步研究
    現(xiàn)有的研究在建立基于馬爾科夫鏈的老化模型時,，考慮了自然老化狀態(tài)、隨機故障狀態(tài),、維修狀態(tài)及具體故障狀態(tài)等,，所提出的狀態(tài)模型都有各自的側重點,，但卻無法形成一個故障狀態(tài)相對完善的機組狀態(tài)模型。而風力發(fā)電機組作為一個復雜的系統(tǒng),，故障模式十分復雜,，囊括所有的故障狀態(tài)是不可能的。所以,，在選擇具體故障狀態(tài)時,，可以根據專家經驗并結合人工智能方法處理歷史數據，選擇對機組運行影響較大的故障,，分析故障間的關系,，以此來建立狀態(tài)模型對優(yōu)化檢修策略更具實際意義。
　從國內外基于馬爾科夫過程的風電機組檢修策略的研究中可以發(fā)現(xiàn),，馬爾科夫理論多用于分析某臺機組,，甚至是某個部件，如齒輪箱,。對于當前風力發(fā)電機組檢修所面臨的困難,，如每次維修停機造成的生產損失、拆裝花費的巨額成本等,，僅考慮某臺機組或某一個部件的最低檢修成本是遠遠不夠的,。而隨著海上風電場的快速發(fā)展，聯(lián)合維護多臺機組以更大程度地節(jié)約檢修成本,，對未來風電行業(yè)的發(fā)展具有重要意義,。
    大型風電機組由多種元部件構成，它們之間的相互耦合關系構成了一個復雜的網絡,。在評估其狀態(tài)時可以通過將復雜網絡理論與馬爾科夫過程理論相結合,，建立一個涵蓋多臺風電機組的綜合狀態(tài)模型。如何將此思想應用到多臺風電機組組成的系統(tǒng)中,，提出相應的狀態(tài)評估模型,，并基于此模型研究一種適合風力發(fā)電機組聯(lián)合檢修的優(yōu)化策略，是一個值得思考的方向,。
參考文獻
[1] 邱仕義．電力設備可靠性維修[M]．北京：中國電力出版社,，2004．
[2] 胡奇英，劉建庸．馬爾科夫決策過程引論[M]．西安：西安電子科技大學出版社,， 2000．
[3] 仵博,，吳敏．部分可觀察馬爾可夫決策過程研究進展[J]．計算機工程與設計，2007,，28(9)：2116-2119,，2126．
[4] 王韶，周家啟．雙回平行輸電線路可靠性模型[J]．中國電機工程學報,，2003,，23(9)：53-56．
[5] 孫福壽,， 汪雄海． 一種分析繼電保護系統(tǒng)可靠性的算法[J]．電力系統(tǒng)自動化，2006,，30(16)：32-35．
[6] 廖瑞金,，肖中男，鞏晶,，等．應用馬爾科夫模型評估電力變壓器可靠性[J]． 高電壓技術,，2010，36(2)：322-328．
[7] 聶雅卓,，周步祥,，林楠，等．考慮轉供容量約束的配電網馬爾可夫可靠性算法[J]．電力系統(tǒng)保護與控制,，2011,，39(13)：59-63．
[8] ARABIAN H H，ORAEE H,，TAVNER P J．Wind turbine productivity considering electrical subassembly reliability[J]．Renewable Energy,，2010(35)：190-197．
[9] 李大字,，馮園園,，劉展，等．風力發(fā)電機組可靠性建模與維修策略優(yōu)化[J]．電網技術,，2011,，35(9)：122-127．
[10] MCMILLAN D，AULT G W． Quantification of condition monitoring benefit for offshore wind turbines[J]． Wind Engineering,，2007,，4(31)：267-285．
[11] Wu Yanru，Zhao Hongshan． Optimization maintenance of  wind turbines using Markov decision process[C]. 2010 International Conference on Power System Technology,，Hangzhou,，China，October 24-28, PowerCon,，2010：1-6．
[12] CHAN G K,，ASGARPOOR S． Optimum maintenance policy with Markov processes[J]． Electric Power Systems Research，2006(76)：452-456．
[13] Ge Haifeng,，TOMASEVICZ C L,，ASGARPOOR S． Optimum maintenance policy with inspection by semi-markov  decision processes[C]. 2007 North American Power Symposium(NAPS)：541-546.
[14] 蘇春，周小荃．基于半馬爾科夫決策過程的風力機狀態(tài)維修優(yōu)化[J]． 機械工程學報,，2012,，48(2)：44-49．
[15] BYON E，NTAIMO L,，DING Y． Optimal maintenance strategies for wind turbine systems under stochastic weather conditions[J]． IEEE Transactions on Reliability,，2010,，59(2)：393-404．
[16] BYON E， DING Y． Season-dependent condition-based maintenance for a wind turbine using a partially observed  Markov decision process[J]． IEEE Transactions on Power Systems,，2010,，25(4)：1823-1834．