摘 要：針對(duì)目前多傳感器數(shù)據(jù)融合過(guò)程中傳感器對(duì)某一狀態(tài)量測(cè)量時(shí)精度較低的問(wèn)題,，提出了基于最小二乘原理的多傳感器加權(quán)數(shù)據(jù)融合算法,。該方法利用最小二乘原理和方差的遺忘信息,通過(guò)均方誤差比較，計(jì)算出各個(gè)傳感器的權(quán)重之后進(jìn)行加權(quán)融合,。該算法既考慮了歷時(shí)信息的作用,又考慮了環(huán)境噪聲和新采樣值的影響,，增強(qiáng)了對(duì)環(huán)境監(jiān)測(cè)的敏感性。相比同類融合方法,，該方法具有較高的精度,，最后仿真結(jié)果也直觀地說(shuō)明了該方法的有效性。
關(guān)鍵詞：數(shù)據(jù)融合,；多傳感器,；均方誤差；最小二乘

     在自動(dòng)化系統(tǒng)或科學(xué)實(shí)驗(yàn)中,，需要用多個(gè)傳感器在不同的方位對(duì)同一目標(biāo)參數(shù)進(jìn)行測(cè)量,，但由于傳感器所處的方位不同和傳感器自身質(zhì)量的差異，以及受一些無(wú)法控制的隨機(jī)因素的作用,，在實(shí)際中各個(gè)傳感器所測(cè)量的參數(shù)值必存在偏差,，這樣就存在如何確定對(duì)測(cè)量數(shù)據(jù)進(jìn)行融合的問(wèn)題[1],。多傳感器數(shù)據(jù)融合就是將來(lái)自多個(gè)傳感器的數(shù)據(jù)或信息進(jìn)行綜合處理，所獲得的結(jié)果比單一傳感器測(cè)量值更為準(zhǔn)確,，能夠更靈敏地檢測(cè)動(dòng)態(tài)系統(tǒng)的變化,。
    在多傳感器加權(quán)融合估計(jì)中，關(guān)鍵是如何為各傳感器分配合適的權(quán)重,。加權(quán)平均法不考慮各測(cè)量數(shù)據(jù)的準(zhǔn)確性,，取同樣的權(quán)值直接求平均值，該算法計(jì)算簡(jiǎn)單,，實(shí)現(xiàn)較為容易,，但是誤差較大。參考文獻(xiàn)[2]提出一種相關(guān)估計(jì)器,，融合了最小均方估計(jì)(LMS)和小波降噪的方法,，對(duì)多個(gè)輸入進(jìn)行算術(shù)平均，所得的平均值使用小波降噪濾波器進(jìn)行降噪,。由于LMS估計(jì)中采用的是算術(shù)平均法,，因此不是最優(yōu)估計(jì)[2]。參考文獻(xiàn)[3]主要針對(duì)恒窗長(zhǎng)方差運(yùn)算對(duì)噪聲變化跟蹤能力不強(qiáng)的缺點(diǎn)提出了自適應(yīng)窗長(zhǎng)方差估計(jì)在多傳感器數(shù)據(jù)融合中的應(yīng)用,。該算法能靈敏地跟蹤傳感器測(cè)量噪聲的突變,，同時(shí)不依賴于初始窗長(zhǎng)的設(shè)定，能自動(dòng)收斂到合適的窗長(zhǎng),，該算法主要用于非平穩(wěn)信號(hào)多傳感器數(shù)據(jù)融合[3],。參考文獻(xiàn)[4-6]采用基于最小二乘原理融合算法，推導(dǎo)出各個(gè)傳感器的權(quán)系數(shù)與測(cè)量方差的關(guān)系,，從而對(duì)各傳感器的權(quán)值進(jìn)行合理的分配,。參考文獻(xiàn)[7]提出了迭代計(jì)算各節(jié)點(diǎn)測(cè)量數(shù)據(jù)的無(wú)偏估計(jì)值，以歸一化后的各傳感器測(cè)量值與無(wú)偏估計(jì)的歐氏距離作為權(quán)值進(jìn)行加權(quán)平均,。參考文獻(xiàn)[8]提出了一種分批估計(jì)法,通過(guò)將各傳感器均分成兩批,，在計(jì)算每批的樣本均值和樣本方差后采用方差加權(quán)進(jìn)行融合處理。參考文獻(xiàn)[9-11]提出了小波去噪法,，通過(guò)去除測(cè)量中的噪聲,，進(jìn)行數(shù)據(jù)融合。參考文獻(xiàn)[12-14]提出了卡爾曼濾波法,，利用卡爾曼濾波器及其估計(jì)誤差協(xié)方差陣分別與傳感器及其測(cè)量方差相對(duì)應(yīng),，對(duì)多組卡爾曼濾波加權(quán)融合。本文采用了基于最小二乘原理多傳感器加權(quán)數(shù)據(jù)融合算法,，綜合考慮傳感器的內(nèi)部噪聲與環(huán)境干擾等多種因素,充分利用測(cè)量數(shù)據(jù)中的冗余信息,，使冗余系統(tǒng)測(cè)量數(shù)據(jù)的估計(jì)進(jìn)一步提高。


1.3 遺忘因子σ選取
    遺忘因子的作用是加強(qiáng)新的數(shù)據(jù)提供的信息量,，逐漸削弱舊的數(shù)據(jù),，以突出新的數(shù)據(jù),。它能綜合考慮傳感器的內(nèi)部噪聲與環(huán)境干擾等多種因素，實(shí)時(shí)方差的利用增強(qiáng)了對(duì)環(huán)境干擾的敏感性,，歷次方差則更好地體現(xiàn)了傳感器自身因素對(duì)測(cè)量值的影響,。根據(jù)公式:
    
2 算法驗(yàn)證與仿真
    本文用Matlab軟件對(duì)上述理論推導(dǎo)結(jié)果作仿真驗(yàn)證。設(shè)待測(cè)信號(hào)的真值為y(t)=1+sint,被6個(gè)傳感器所測(cè)量,。假設(shè)6個(gè)傳感器相互之間互不影響,，它們分別單獨(dú)地加入均值為0、方差為0.01,、0.03,、0.05、0.10,、0.15的高斯白噪聲,并分別均勻地采集了300個(gè)點(diǎn),。圖1為4種方法在一次試驗(yàn)中均方誤差各個(gè)時(shí)刻曲線比較圖。

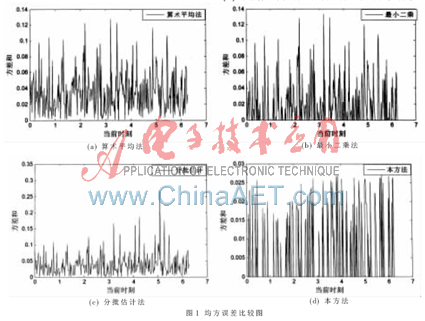
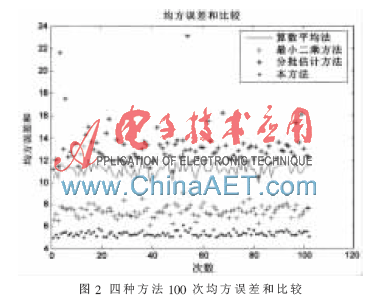
    從圖1中可以看出,，各個(gè)時(shí)刻均方誤差由大到小依次為算術(shù)平均法,、最小二乘、分批估計(jì)與本方法,。利用基于最小二乘和遺忘因子方法均方誤差與各個(gè)時(shí)刻比較平均,。把各個(gè)時(shí)刻的均方誤差相加，算術(shù)平均法,、最小二乘,、分批估計(jì)和本方法隨機(jī)試驗(yàn)100次得到圖形如圖2所示。從圖2中可以看出本方法均方誤差和最小,。

    多傳感器在對(duì)某一參數(shù)進(jìn)行測(cè)量時(shí),，因受傳感器自身因素和環(huán)境的影響,，會(huì)有不同的測(cè)量結(jié)果,。多傳感器數(shù)據(jù)融合可以有效地利用重復(fù)冗余的信息，提高量測(cè)信息的估計(jì)精度,。本文提出了基于最小二乘和遺忘因子的多傳感器數(shù)據(jù)融合算法,，對(duì)實(shí)驗(yàn)數(shù)據(jù)進(jìn)行了融合處理，可以看出與其他3種方法相比估計(jì)精度顯著提高,。本方法可以用于獲取被測(cè)參數(shù)量估計(jì)值的動(dòng)態(tài)系統(tǒng)中,，因此該算法具有較強(qiáng)的實(shí)用性。
參考文獻(xiàn)
[1] 劉建書(shū),李人厚,常宏.基于相關(guān)性函數(shù)和最小二乘的多傳感器數(shù)據(jù)融合[J].控制與決策,2006,21(6):714-716.
[2] MAJUMDER S,SCHEDINGAND S,DURRANT-WYHTE H F.Multi-sensor data fusion for underwater navigation[J].Robotics and Autonomous System,2001(35):97-108.
[3] 張怡,賈民平.自適應(yīng)窗長(zhǎng)方差估計(jì)在多傳感器數(shù)據(jù)融合中的應(yīng)用[J].傳感技術(shù)學(xué)報(bào),2008,21(8)：1398-1401.
[4] 仲崇權(quán),張立勇,楊素英,等.基于最小二乘原理的多傳感器加權(quán)融合算法[J].儀器儀表學(xué)報(bào),2003,24(4):427-429.
[5] Song Kaichen, Nie Xili. Adaptive fusion atgorithms based on weighed least square method[J]. Chinese Journal of Mechanical Engineering,2006,19(3)：451-454.
[6] 李雪蓮,孫堯,莫宏偉.基于最小二乘的冗余信息數(shù)據(jù)融合算法實(shí)現(xiàn)[J].計(jì)算機(jī)工程與應(yīng)用,2009,45(15)：34-39.
[7] 馬琦,，張記龍,，王志斌.無(wú)線傳感器網(wǎng)絡(luò)簇內(nèi)自適應(yīng)融合算法研究[J].計(jì)算機(jī)應(yīng)用研究,2009，26(7)：2502-2503.
[8] 張西良,孫優(yōu).無(wú)線傳感器網(wǎng)絡(luò)基于定向擴(kuò)散與分批估計(jì)的數(shù)據(jù)融合算法[J].傳感器與儀器儀表,，2006,22(9)：173-176.
[9] 李超,胡謀法,，劉朝軍,，等.基于小波的多傳感器空間目標(biāo)數(shù)據(jù)融合算法[J].信號(hào)處理,2006,22(4):203-207.
[10] Xu Lijun, Zhang Jianqiu,Yan Yong. A wavelet-based mutilsensor data fusion algorithm[J]. IEEE Transactions on  Instrumentation and Measurement, 2004,53(6):1539-1545.
[11] 高羽，張建秋.小波變換域估計(jì)觀測(cè)噪聲方差的Kalman濾波算法及其在數(shù)據(jù)融合中的應(yīng)用[J].電子學(xué)報(bào),2007,35(1):108-111.
[12] SUN S L, DENG Z L. Multi-sensor optimal information  fusion kalman filter[J]. A Utomatica,2004,40(6):1017-1023.
[13] SUN S Ｌ． Multi-sensor information fusion while noise filter weighted by scalars based on Kalman predictor[J]. Automation,2004,40(8):1447-1453.
[14] 蔡鶴皋,，金明河,，金峰.卡爾曼濾波與多傳感器數(shù)據(jù)融合技術(shù)[J].模式識(shí)別與人工智能,2009,13(3):248-254.
[15] 施雨,李耀武.概率論與數(shù)理統(tǒng)計(jì)應(yīng)用[M].西安：西安交通大學(xué)出版社,1998.