摘  要： 針對(duì)紋理圖像分割問(wèn)題的研究，經(jīng)典的多尺度MRF方法是對(duì)不同尺度的紋理特征僅通過(guò)多尺度序列下的MRF鄰域系統(tǒng)進(jìn)行描述,。為了更加準(zhǔn)確地描述紋理特征,，將從空間分布特性與MRF鄰域系統(tǒng)兩個(gè)方面綜合考慮,，提出一種帶有聯(lián)合灰度信息的灰度共生矩陣與多尺度MRF相結(jié)合的方法。實(shí)驗(yàn)結(jié)果表明,，該方法能夠有效地提高分割準(zhǔn)確度,。
關(guān)鍵詞： 紋理圖像分割；灰度共生矩陣,；多尺度,；MRF

　紋理作為一種自然屬性，在一定程度上反映了物體的特征,，并且紋理具有抗遮擋能力強(qiáng),、受環(huán)境影響小等特點(diǎn)，因此常被用于區(qū)分背景與其他物體,。通常情況下,，紋理可以采用基于模型的MRF（Markov Random Field）方法進(jìn)行描述。單尺度MRF模型是空域模型,，常采用貝葉斯法進(jìn)行圖像分割,。多尺度MRF模型是在不同分辨率的圖像上進(jìn)行分析，它能捕捉到不同分辨率圖像的結(jié)構(gòu)信息以及具備更強(qiáng)的空間描述能力,，并且還具有計(jì)算復(fù)雜度低,、收斂速度快、減少過(guò)分割現(xiàn)象和較強(qiáng)的抗噪性能等特點(diǎn)[1],，因此多尺度MRF圖像分割受到廣泛關(guān)注,。近幾年研究中，陳曉惠等人[2]將形態(tài)小波域多尺度馬爾可夫模型應(yīng)用于紋理圖像分割中,，該模型結(jié)合了形態(tài)小波和MRF各自的優(yōu)勢(shì),，能夠?qū)D像進(jìn)行非線性多尺度分解，因此提高了對(duì)紋理特征的描述,。對(duì)于多尺度MRF分割方法,，不同尺度的紋理特征僅通過(guò)多尺度序列下的MRF鄰域系統(tǒng)進(jìn)行描述，并且在起始分割中僅考慮了灰度特征而忽略了鄰域系統(tǒng)特性和像素在空間中的排列信息,。在統(tǒng)計(jì)方法中,，灰度共生矩陣能夠有效地從空間中提取紋理特征[3]，并且灰度共生矩陣與MRF之間存在關(guān)聯(lián)性,，其中3個(gè)不相關(guān)的二次統(tǒng)計(jì)量就可作為紋理特征描述,。僅用灰度信息、距離判定,、無(wú)鄰域系統(tǒng)相關(guān)性或空間相關(guān)性描述紋理特征,，具有一定的局限性。為了解決該問(wèn)題，本文提出將帶有灰度信息的灰度共生矩陣與多尺度MRF相結(jié)合的方法進(jìn)行紋理圖像分割,。
1 多尺度MRF與灰度共生矩陣下的紋理結(jié)構(gòu)
1.1 多尺度MRF
　原始圖像經(jīng)過(guò)小波分解后可得到具有不同尺度的圖像數(shù)據(jù),，并依據(jù)尺度大小關(guān)系組成金字塔結(jié)構(gòu)。然后,，在最大尺度圖像上利用低頻信號(hào)建立最大尺度下的MRF,，再依次以上層分割結(jié)果作為下層分割的基礎(chǔ)[4]。
　圖像的多尺度MRF模型是通過(guò)建立特征場(chǎng)與標(biāo)號(hào)場(chǎng)來(lái)描述數(shù)據(jù)信息的,。多分辨率特征場(chǎng)的多尺度序列表示為Y={Y0,，Y1，…,，YJ-1},，標(biāo)號(hào)場(chǎng)表示為X={X0，X1,，…,，XJ-1}，其中特征場(chǎng)描述數(shù)據(jù)的特征,，標(biāo)號(hào)場(chǎng)描述分割結(jié)果的類別[2]。通常采用MRF二階鄰域系統(tǒng)（即某一像素與其鄰近像素的關(guān)系）的形式來(lái)表示紋理特征,，如圖1所示,。由于二階鄰域系統(tǒng)未能詳細(xì)地描述出像素的空間排列信息，因此在分割過(guò)程中可能會(huì)漏掉某些特征信息,。

　與MRF不同,，二次統(tǒng)計(jì)量是在空間分布上對(duì)紋理信息進(jìn)行描述[5]?；叶裙采仃囋诿枋黾y理時(shí)缺少了局部細(xì)節(jié)信息,，可以通過(guò)MRF的鄰域系統(tǒng)來(lái)彌補(bǔ)。反之,，MRF空間信息的缺失也可以通過(guò)灰度共生矩陣得到補(bǔ)充,。
2 基于灰度共生矩陣和多尺度MRF的紋理圖像分割
　以灰度共生矩陣為基礎(chǔ)提取的3個(gè)互不相關(guān)的二次統(tǒng)計(jì)量熵、對(duì)比度與相關(guān)性,，可以很好地從空間分布方面來(lái)描述圖像的紋理[6],。為了更加準(zhǔn)確地描述紋理特征，可將3個(gè)互不相關(guān)的統(tǒng)計(jì)量與灰度信息共同用于描述最大尺度下的紋理信息,，形成特征矩陣C=[f1 f2 f3 f4],，然后進(jìn)行FCM聚類。

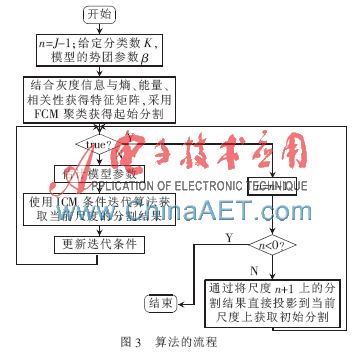
　基于灰度共生矩陣和多尺度MRF圖像分割方法流程如圖3所示,，具體步驟如下：
?。?）設(shè)定圖像的分類數(shù)K、勢(shì)團(tuán)參數(shù)β以及算法迭代次數(shù)。
?。?）對(duì)圖像作n=J-1層小波分解,，利用灰度共生矩陣提取特征，并與灰度信息共同獲得特征矩陣,，利用FCM獲得起始分割結(jié)果,。
　（3）由聚類算法的標(biāo)號(hào)計(jì)算出尺度J上的標(biāo)號(hào)場(chǎng)能量,，進(jìn)行參數(shù)估計(jì),，計(jì)算特征場(chǎng)能量，利用能量最小原則,，得出該尺度分割結(jié)果,。
　（4）將該尺度的計(jì)算結(jié)果直接映射到最鄰近的高分辨率圖像上作為初始分割,。
?。?）進(jìn)行參數(shù)估計(jì)，計(jì)算標(biāo)號(hào)場(chǎng)能量,，計(jì)算特征場(chǎng)能量,，更新迭代條件當(dāng)能量最小時(shí)計(jì)算停止。

3 實(shí)驗(yàn)結(jié)果與分析
　選取256×256的合成紋理圖像,、256×256的遙感圖像和來(lái)自Berkeley圖像庫(kù)編號(hào)為86016的481×321自然景物紋理圖像,。實(shí)驗(yàn)選取灰度共生矩陣步長(zhǎng)為1，方向選取0°,、45°,、90°、135°,。紋理合成圖像灰度共生矩陣選取7×7的滑動(dòng)窗口,，勢(shì)團(tuán)參數(shù)=5.5，迭代100次,；遙感圖像選取5×5的滑動(dòng)窗口,，勢(shì)團(tuán)參數(shù)β=0.9，迭代50次,；自然景物圖像選擇33窗口,，勢(shì)團(tuán)參數(shù)β=0.9，迭代50次,。實(shí)驗(yàn)平臺(tái)為Matlab 7.8.0,，圖4為分割效果圖，其中,，第1列至第5列分別為：實(shí)驗(yàn)原圖,、手工標(biāo)注圖,、灰度共生矩陣分割結(jié)果、多尺度MRF分割結(jié)果,、本文方法分割結(jié)果,。為了能夠定量分析分割結(jié)果，本文將采用整體分類精度和Kappa系數(shù)作為評(píng)價(jià)指標(biāo),，結(jié)果如表1所示,。

　從表1可以看出，針對(duì)3種類型紋理圖像,，本文方法獲得的分割結(jié)果要明顯優(yōu)于灰度共生矩陣法與多尺度MRF法,。其中，對(duì)于合成紋理圖像,，本文方法的整體分類精度為99.03%,，Kappa系數(shù)為97.95%，均高于灰度共生矩陣法與多尺度MRF法,；對(duì)于遙感圖像,，本文方法的整體分類精度為96.66%，Kappa系數(shù)為90.12%,，均高于灰度共生矩陣法與多尺度MRF法,；對(duì)于自然景物圖像，本文方法的整體分類精度為98.34%,，Kappa系數(shù)為96.13%,，也均高于灰度共生矩陣法與多尺度MRF法。綜合考慮,，在平均整體分類精度方面，本文方法比多尺度MRF法高出2.96%,，比灰度共生矩陣法高出5.94%,；在平均Kappa系數(shù)方面，本文方法比多尺度MRF法高出1.72%,，比灰度共生矩陣法高出12.12%,。實(shí)驗(yàn)表明，本文提出的紋理圖像分割方法不僅提高了分割準(zhǔn)確度,，還提高了分割的一致性,。
　本文提出了一種基于灰度共生矩陣和多尺度MRF紋理圖像的分割方法。首先,，采用小波分解獲得圖像各個(gè)尺度的數(shù)據(jù)信息,，之后在最大尺度上結(jié)合灰度信息以及由灰度共生矩陣獲得的二次統(tǒng)計(jì)量進(jìn)行FCM聚類，作為最大尺度上MRF的起始分割,；其次,，依照起始分割的標(biāo)號(hào)再進(jìn)行當(dāng)前尺度MRF的分割，建立特征場(chǎng)與標(biāo)號(hào)場(chǎng)，獲得當(dāng)前尺度最終的分割結(jié)果,；最后,，當(dāng)前分割結(jié)果作為鄰近高分辨率圖像的起始分割再進(jìn)行優(yōu)化。實(shí)驗(yàn)表明,，本文方法分割紋理圖像的準(zhǔn)確度與Kappa系數(shù)高于多尺度MRF方法和灰度共生矩陣的方法,。在后續(xù)的研究中，將探討如何提高算法的運(yùn)算速度,。
參考文獻(xiàn)
[1] 劉國(guó)英,，馬國(guó)銳，王雷光,，等.基于Markov隨機(jī)場(chǎng)的小波域圖像建模及分割[M].北京：科學(xué)出版社,，2010.
[2] 陳曉惠，鄭晨,，段汕,，等.形態(tài)小波域多尺度馬爾可夫模型在紋理圖像分割中的應(yīng)用[J].中國(guó)圖象圖形學(xué)報(bào)，2011,，16（5）：761-766.
[3] 韋玉春,，湯國(guó)安，楊昕,，等.遙感數(shù)字處理教程[M].北京：科學(xué)出版社,，2009.
[4] Zheng C， Liu G,， Hu Y,， et al. Image segmentation based on multiresolution Markov random field with fuzzy constraintin wavelet domain[J]. IET Image Process，2012,，6（3）：213-221.
[5] MRIDULA J,， KUNDAN C， DIPTI P. Combining GLCM features and Markov random field model for colour textured image segmentation[C]. IEEE Conference on Devices and Communications（ICDeCom2011）,，2011：1-5.