文獻(xiàn)標(biāo)識碼: A
文章編號: 0258-7998(2014)01-0047-03
雙基地雷達(dá)的收發(fā)系統(tǒng)分置兩地,接收機(jī)靜默,這種體制的雷達(dá)在抗后向有源干擾和抗反輻射導(dǎo)彈方面具有明顯的優(yōu)勢。由于隱身飛行器的隱身效果主要表現(xiàn)在鼻錐方向的后向散射上,而雙基地雷達(dá)的接收站接收到的是目標(biāo)在其他方向的散射,其等效的雙基地雷達(dá)目標(biāo)的RCS(雷達(dá)截面積)較后向散射的RCS大。因此,在抗隱身方面,雙基地雷達(dá)也有潛力[1]。
但由于雙基地雷達(dá)采用收發(fā)分置的體制,這就增加了雙基地雷達(dá)目標(biāo)參數(shù)計(jì)算的復(fù)雜性。為了實(shí)現(xiàn)對目標(biāo)的良好跟蹤,必須對目標(biāo)的參數(shù)進(jìn)行實(shí)時(shí)測算。目前雷達(dá)目標(biāo)參數(shù)的計(jì)算大多是通過軟件的方式來實(shí)現(xiàn)的,但是隨著雷達(dá)數(shù)據(jù)率的不斷提高,軟件方法越來越不能滿足雷達(dá)信號處理的實(shí)時(shí)性與高速性要求,所以有必要用硬件來實(shí)現(xiàn)實(shí)時(shí)計(jì)算。但雙基地雷達(dá)目標(biāo)速度計(jì)算涉及復(fù)雜的數(shù)學(xué)運(yùn)算,若硬件實(shí)時(shí)計(jì)算采用一般的算法來實(shí)現(xiàn),不僅資源消耗大,而且影響運(yùn)算速度。
由此,本文根據(jù)CORDIC算法通過簡單的移位和加減運(yùn)算就能計(jì)算包括乘、除、正余弦、反正切、向量旋轉(zhuǎn)以及指數(shù)運(yùn)算等的優(yōu)點(diǎn),將CORDIC算法引入到雙基地雷達(dá)目標(biāo)速度的計(jì)算中,可大大降低雙基地雷達(dá)目標(biāo)速度計(jì)算的復(fù)雜度,便于硬件實(shí)現(xiàn),從而可以有效提高雙基地雷達(dá)的跟蹤精度。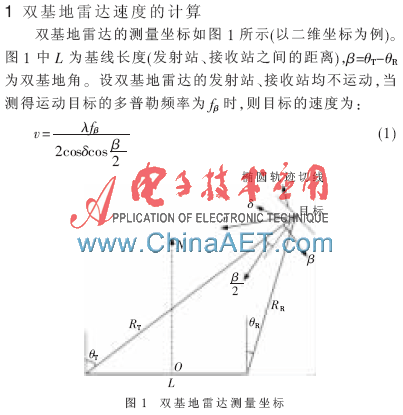


3 雙基地雷達(dá)目標(biāo)速度計(jì)算模塊的設(shè)計(jì)
3.1 角度預(yù)處理模塊的設(shè)計(jì)
在雙基地雷達(dá)目標(biāo)速度的計(jì)算中,β、δ的角度范圍均在0°~180°內(nèi),而CORDIC算法的角度的覆蓋范圍為-99.88°~99.88°,因此在用FPGA模塊進(jìn)行速度計(jì)算時(shí),需要對β、δ進(jìn)行預(yù)處理。
本文在QuartusII 7.2軟件環(huán)境下進(jìn)行FPGA實(shí)現(xiàn),并在EP2C70F896C6芯片上進(jìn)行驗(yàn)證。設(shè)輸入數(shù)據(jù)的長度為17 bit,最高位是符號位,接著是1個(gè)整數(shù)位,低15 bit為小數(shù)位。對于浮點(diǎn)數(shù)計(jì)算占用資源多并且實(shí)現(xiàn)復(fù)雜的問題,解決方法是采用定點(diǎn)運(yùn)算,將浮點(diǎn)數(shù)都擴(kuò)大215倍,最后將輸出的結(jié)果縮小215倍,就得到需要的結(jié)果[5]。由于數(shù)據(jù)用16 bit表示,所以90°表示為(90°×32 768)/360°=8 192。進(jìn)行角度預(yù)處理的關(guān)鍵VHDL代碼如下:
IF (Zin≥0) THEN
Zin0<=Zin-8192
ELSE Zin0<=Zin+8192
END IF
IF (Zin≥0) THEN
Xout15<=-Yout15_Zin0
Yout15<=Xout15_Zin0
ELSE
Xout15<=Yout15_Zin0
Yout15<=-Xout15_Zin0
END IF
3.2 正余弦值計(jì)算模塊的設(shè)計(jì)
在雙基地雷達(dá)目標(biāo)速度的計(jì)算中,關(guān)鍵技術(shù)是正余弦值的計(jì)算,正余弦值的計(jì)算速度直接關(guān)系到雙基地雷達(dá)目標(biāo)速度的數(shù)據(jù)率。綜合考慮計(jì)算的速率和FPGA硬件資源的消耗,本文采用流水線結(jié)構(gòu)CORDIC算法來實(shí)現(xiàn)正余弦值的計(jì)算。CORDIC流水線結(jié)構(gòu)利用N個(gè)相同的運(yùn)算單元,讓每次迭代同時(shí)進(jìn)行[6]。用流水線結(jié)構(gòu)實(shí)現(xiàn)CORDIC算法的結(jié)構(gòu)圖如圖3所示。其中,每一次迭代都由一個(gè)單獨(dú)的CORDIC單元來完成,每一次迭代后都有一個(gè)數(shù)據(jù)鎖存器。



從仿真結(jié)果可以看出,本文設(shè)計(jì)的流水線結(jié)構(gòu)CORDIC模塊計(jì)算出的正余弦值計(jì)算精度很高,可以滿足雙基地雷達(dá)計(jì)算精度的要求。
3.3 速度計(jì)算總體模塊的設(shè)計(jì)
前面已經(jīng)完成了正余弦值計(jì)算模塊和角度預(yù)處理模塊的設(shè)計(jì),最后只需要對運(yùn)算模塊進(jìn)行設(shè)計(jì),再將正余弦值計(jì)算模塊、角度預(yù)處理模塊和運(yùn)算模塊結(jié)合起來就可以完成速度計(jì)算總體模塊的設(shè)計(jì)。運(yùn)用原理圖設(shè)計(jì)法,用加法器、乘法器和移位寄存器可以方便地實(shí)現(xiàn)運(yùn)算模塊。運(yùn)算模塊的功能是將正余弦值計(jì)算模塊計(jì)算結(jié)果與雙基地雷達(dá)的波長和目標(biāo)的多普勒頻率進(jìn)行相應(yīng)的計(jì)算,最終得到雙基地雷達(dá)目標(biāo)的速度。
雙基地雷達(dá)的波長和目標(biāo)的多普勒頻率均用17 bit浮點(diǎn)數(shù)表示。設(shè)波長λ=3 cm,多普勒頻率為fβ=9 kHz,雙基地角β=60°,目標(biāo)速度矢量與雙基地角等分線之間的夾角?啄=57°。在QuartusII 7.2軟件中利用設(shè)計(jì)的速度計(jì)算總體模塊對目標(biāo)速度進(jìn)行仿真計(jì)算,可計(jì)算得到目標(biāo)速度v=285.9 m/s,與理論值v0=286.1 m/s十分接近,計(jì)算結(jié)果精度較高,可滿足雙基地雷達(dá)測速的精度要求。
另外,QuartusII 7.2的編譯報(bào)告顯示,實(shí)現(xiàn)此速度計(jì)算模塊消耗邏輯單元3 965個(gè),占總邏輯單元的6%。而若用傳統(tǒng)的查找表法先計(jì)算出角度正余弦值,再計(jì)算雙基地雷達(dá)目標(biāo)的速度,則需要較大的ROM來存儲角度的正余弦值,并且還會消耗較多的乘法器。所以采用CORDIC算法計(jì)算雙基地雷達(dá)目標(biāo)速度在保證計(jì)算精度的同時(shí),還能減少資源消耗,提高工作速度,提高了雙基地雷達(dá)的數(shù)據(jù)率。
本文根據(jù)雙基地雷達(dá)測速的要求,針對傳統(tǒng)速度計(jì)算方法速度慢、資源消耗大的缺點(diǎn),基于CORDIC算法設(shè)計(jì)了雙基地雷達(dá)測速模塊,并進(jìn)行了仿真驗(yàn)證和硬件FPGA的實(shí)現(xiàn)。仿真結(jié)果表明,本文設(shè)計(jì)的雙基地雷達(dá)測速模塊精度高、速度快、資源消耗少,能滿足雙基地雷達(dá)測速的實(shí)際要求。另外,本文利用VHDL語言和原理圖對測速模塊進(jìn)行設(shè)計(jì),采用模塊化設(shè)計(jì)思想,使得本設(shè)計(jì)靈活簡便,可移植性強(qiáng),通用性好,可以很好地應(yīng)用到實(shí)際工程領(lǐng)域中。
參考文獻(xiàn)
[1] 丁鷺飛,耿富錄,陳建春.雷達(dá)原理[M].北京:電子工業(yè)出版社,2009.
[2] VOLDER J E.The cordic trigonometric computing technique[J]. TRE Trans.Elec.Comp.,1959,8(3):330-334.
[3] VANKKA J.Methods of mapping from phase to sine amplitude in direct digital synthesis[C].Proc.of the 1996 IEEE International Frequency Control Symposium,USA:IEEE,1996:942-950.
[4] 駱艷卜,張會生,張斌,等.一種CORDIC算法的FPGA實(shí)現(xiàn)[J].計(jì)算機(jī)仿真,2009,26(9):305-307.
[5] 岳鴻鵬,王和明,任璟.一種基于CORDIC算法的復(fù)乘模塊設(shè)計(jì)及其FFT應(yīng)用[J].微電子學(xué),2010,40(4):539-542.
[6] 何賓.FPGA數(shù)字信號處理實(shí)現(xiàn)原理及方法[M].北京:清華大學(xué)版社,2010.

