摘 要: 提出了一種在非視距(NLOS)環(huán)境下對移動臺的定位算法。首先利用小波分析對AOA的測量值中的NLOS進行修正,再利用最小二乘(LS)算法確定移動臺的位置。仿真結果表明,該算法能夠有效地降低非視距環(huán)境誤差的影響,性能優(yōu)于基于AOA的LS算法以及神經(jīng)網(wǎng)絡算法。
關鍵詞: 非視距傳播;小波分析;最小二乘法;AOA
隨著現(xiàn)在移動通信技術的高速發(fā)展,很多運營商提供的通信服務也越來越多元化,尤其是無線定位技術在諸多領域里都有了非常普遍的應用,如今,移動臺的主要定位原理方法有:到達時間(TOA)定位、到達時間差(TDOA)定位、到達角(AOA)定位以及到達角與到達時間混合定位[1]等。
出現(xiàn)定位誤差的主要因素有測量器材引起的隨機誤差,還有無線電波的非視距傳播(NLOS)效應和多徑效應、多址干擾以及遠近效應的影響,從而使得定位估計出現(xiàn)較大的偏差。在這些誤差中,非視距傳播效應是造成定位誤差的首要原因。現(xiàn)有的AOA定位算法有基于神經(jīng)網(wǎng)絡定位[2]、基于遺傳算法定位[3]以及其他混合定位算法[3-5]。神經(jīng)網(wǎng)絡的AOA定位算法因前期訓練時間長,具有收斂速度慢、神經(jīng)網(wǎng)絡機構選擇不一等缺陷,而遺傳算法穩(wěn)定性較差。基于小波分析[6]是一種新的處理信號噪聲方法,通過進行變換能夠充分突出問題,某些方面的特征在信號的組成部分中,噪聲都處在信號的高頻部分,有用信號的頻譜處在低頻部分,小波分析就是通過母小波函數(shù)將信號進行平移和尺度變化,得到小波函數(shù)的疊加,在不同尺度用小波對其逐步分析以減小誤差,使得信號特征明顯、計算速度快且精度高。本文即采用小波變換法,先用小波分析其測量數(shù)據(jù)并進行優(yōu)化處理,在此基礎上使用最小二乘算法進行位置估計,并對該算法進行了仿真和分析。
1 信道模型
本文采用基于幾何結構的單次反射統(tǒng)計信道模型(GBSB),在無線定位研究中,這是一種常用的信道模型,其中宏蜂窩環(huán)境適合使用基于幾何結構的單次反射圓模型(GBSBCM),微蜂窩環(huán)境適合使用基于幾何結構的單次反射橢圓模型。本文主要采用基于幾何結構的GBSBCM,處在城市地區(qū)的微蜂窩環(huán)境來說,反射射頻信號的障礙物比較多,并且移動臺到基站的距離接近于小區(qū)半徑,這樣會產(chǎn)生較大的角測量誤差,因此這種情形下,基于AOA的單一定位方法沒有實際意義。
因宏蜂窩環(huán)境的基站相對在很高的位置,小區(qū)的半徑遠小于基站的高度,障礙物比較少,多處于移動臺附近,由NLOS效應引起的誤差較小,因此本文主要采用基于幾何結構的GBSBCM,如圖1所示。引起反射的障礙物均勻分布在中心為MS,半徑為R的圓上,實際應用中R的值由實際測得數(shù)據(jù)統(tǒng)計得出。



2.2.2 基于小波分析的AOA定位算法
因為對于AOA的LS算法誤差相對較小,所以在可視距(LOS)環(huán)境下具有優(yōu)良的的定位效果,然而對于NLOS環(huán)境下,那么最小二乘LS的算法引起的誤差就相對較大。利用小波分析對在NLOS環(huán)境下的AOA測量信號進行修正,從而減小數(shù)據(jù)中的NLOS誤差,最后在使用LS法來進行定位,這樣就可以有效地達到提高系統(tǒng)定位精度的目的。
定位步驟如下:
(1)假設先測得有K組在NLOS環(huán)境下的AOA數(shù)據(jù),建立小波函數(shù)式對其進行數(shù)據(jù)分解變換得到小波系數(shù)。
(2)利用門限閾值對小波系數(shù)進行處理,重構出AOA數(shù)據(jù)信號。
(3)對重構的AOA數(shù)據(jù)信號應用LS算法進行位置估算。
3 仿真與分析
為了檢驗算法的實際可能性,對于不同的AOA數(shù)據(jù)測量誤差以及在不同小區(qū)半徑下的定位,將本算法與直接采用最小二乘法的定位算法進行了仿真對比[8],如圖3所采用的標準蜂窩網(wǎng)絡結構,BS1(0,0)為服務基站的小區(qū)中心點,并且所有BS與MS之間均存在NLOS,且AOA系統(tǒng)的測量誤差為獨立同分布的均值為0,標準差為0.1 ?滋s(約30 m)的高斯隨機變量。
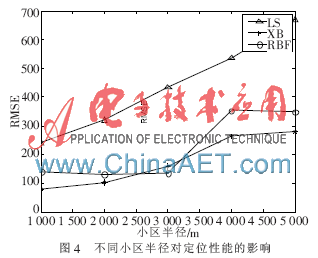
圖4為在不同的小區(qū)半徑下,本文所采用的定位算法與一般所用LS算法定位以及基于神經(jīng)網(wǎng)絡的定位算法[9]結果比較,在不同的小區(qū)半徑下縱坐標顯示為3種算法定位結果的均方誤差值。仿真結果表明,采用本文算法的定位性能比直接采用LS算法及其神經(jīng)網(wǎng)絡算法的要好。當小區(qū)半徑逐步增加,本文算法的誤差增長速度也低于LS算法,在4 km之后誤差增長速度才凸顯。以上說明,采用小波分析預處理數(shù)據(jù)在抑制NLOS誤差上效果顯著,因此對移動臺的定位效果同樣顯著。
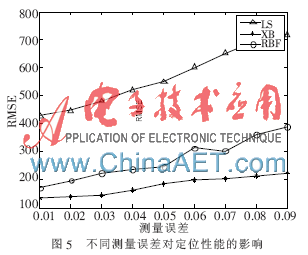
在不同測量誤差下,本文所采用的定位算法與LS算法和基于神經(jīng)網(wǎng)絡算法的結果比較如圖5所示。圖5縱坐標為3種算法在不同測量誤差下定位結果的均方誤差值。從仿真結果來看,當測量誤差逐漸增長時,本文所采用的算法定位效果變化不大,且本文算法的均方誤差增長緩慢,變化幅度不大,而對比其他兩種算法性能逐漸下降,由此說明本文算法能夠明顯地抑制NLOS誤差以及測量誤差,同樣在對移動臺的定位方面效果良好。
在實際應用中,NLOS誤差是影響移動臺定位的主要誤差,一般算法在其影響下定位效果很差,基于神經(jīng)網(wǎng)絡在移動臺定位方面效果明顯,但是因為訓練時間實在太長,收斂速度緩慢,因此無法付出實施。小波分析預處理測量數(shù)據(jù),多分辨、多尺度分析能良好地抑制其誤差,而且處理速度快。本文提出了一種在NLOS環(huán)境下基于小波分析的AOA定位算法,運用閾值對其信號過濾重構,達到消除噪聲的目的,從而使用LS算法進行定位,其效果良好。但是對于小波分析閾值法,在硬閾值函數(shù)存在不連續(xù)性,在軟閾值在小波系數(shù)的估計中存在恒定偏差等,因此有待繼續(xù)研究并改善。
參考文獻
[1] Xie Yaqin, Wang Yan, Zhu Pengcheng,et al,Grid-search-based hybrid TOA/AOA location techniques for NLOS environments[J]. IEEE Communications Letters,2009,13(4):254-256.
[2] 毛勇毅,李明遠,張寶軍.基于RBF神經(jīng)網(wǎng)絡的蜂窩無線定位算法[J].系統(tǒng)工程與電子技術,2008,30(9):1798-1800.
[3] 江波,薛磊.基于遺傳算法的TDOA/AOA定位系統(tǒng)的布站算法[J].計算機工程與應用,2009,45(24):219-221.
[4] 郭麗梅,羅大庸.非視距環(huán)境中TOA/AOA混合定位方法[J].電路與系統(tǒng)學報,2010,5(15):26-30.
[5] 陳奎,黃為勇,田傳耕.基于Matrix Pencil的OFDM信號的TOA/AOA定位[J].計算機應用研究,2013,30(2):534-536.
[6] Mao Jiandong. Noise reduction for lidar returns using local threshold wavelet analysis[J]. Optical and Quantum Electronics. 2012,43(1-5):59-68.
[7] 卓寧.小波分析技術在GPS數(shù)據(jù)預處理中的應用[J].中國慣性技術學報,2009,17(2):184-186.
[8] 叢爽.面向MATLAB工具箱的神經(jīng)網(wǎng)絡理論與應用[M].北京:中國科學技術大學出版社,2009.
[9] Tian Hui, Wang Shuang, Xie Huaiyao. Localization using cooperative AOA approach[J]. Wireless Communications, Networking and Mobile Compution, 2007,9(1):2416-2419.

