摘  要： 基于密度吸引點(diǎn)和其對(duì)相鄰節(jié)點(diǎn)的影響度,，提出了一種密度分布社區(qū)發(fā)現(xiàn)算法。該算法以節(jié)點(diǎn)度數(shù)最大的密度吸引點(diǎn)為初始社區(qū),，訪問社區(qū)的相鄰節(jié)點(diǎn),，把對(duì)社區(qū)影響度最大的節(jié)點(diǎn)加入到社區(qū)中，如果有些節(jié)點(diǎn)對(duì)多個(gè)社區(qū)都有影響,，則把它歸屬為影響度最大的那個(gè)社區(qū)中,，同時(shí)如果兩個(gè)社區(qū)之間的相互影響度很大，可以將這兩個(gè)社區(qū)合并為一個(gè)社區(qū),。將該算法應(yīng)用到Zachary空手道俱樂部網(wǎng)絡(luò)和隨機(jī)無標(biāo)度網(wǎng)絡(luò)中,，實(shí)驗(yàn)表明該算法能夠很好地分出網(wǎng)絡(luò)中的社區(qū)，同時(shí)實(shí)驗(yàn)還發(fā)現(xiàn)社區(qū)的收斂速度與冪率分布特性近似成反比,。
 關(guān)鍵詞： 復(fù)雜網(wǎng)絡(luò),；冪率分布；社區(qū)發(fā)現(xiàn),；密度分布,；影響度

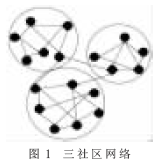
所謂社區(qū)，是指具有共同興趣,、愛好的人或者學(xué)有專精的專業(yè)人士,，通過一定的方式聚集在一起，彼此之間可以溝通、交流,、分享相關(guān)信息,。在現(xiàn)實(shí)世界中，存在著很多這樣的社區(qū),，例如社會(huì)關(guān)系網(wǎng)絡(luò)[1],、神經(jīng)網(wǎng)絡(luò)、食物鏈網(wǎng)絡(luò),、城市交通網(wǎng)絡(luò)等,。在這些社區(qū)中，有著復(fù)雜的內(nèi)部結(jié)構(gòu),，用節(jié)點(diǎn)表示實(shí)體,，用連線表示實(shí)體間的聯(lián)系，社區(qū)內(nèi)部節(jié)點(diǎn)之間的聯(lián)系非常緊密,，社區(qū)之間的聯(lián)系相對(duì)稀疏,。近幾年，隨著網(wǎng)絡(luò)的急速發(fā)展,，網(wǎng)絡(luò)社區(qū)也成為一個(gè)研究熱點(diǎn),，同時(shí)取得了很重要的進(jìn)展，并且發(fā)現(xiàn)了網(wǎng)絡(luò)社區(qū)的很多特點(diǎn),，其中包括小世界特性(即網(wǎng)絡(luò)中節(jié)點(diǎn)之間的平均距離很短,，對(duì)數(shù)依賴于網(wǎng)絡(luò)中的節(jié)點(diǎn)數(shù))、無標(biāo)度特性(即網(wǎng)絡(luò)中節(jié)點(diǎn)的度分布右偏斜,，具備冪函數(shù)或指數(shù)函數(shù)的形式),、聚集性或網(wǎng)絡(luò)傳遞性以及社區(qū)結(jié)構(gòu)特性，大量實(shí)證研究表明,，許多網(wǎng)絡(luò)是異構(gòu)的,，即復(fù)雜網(wǎng)絡(luò)不是大批性質(zhì)相同節(jié)點(diǎn)的隨機(jī)連接,，而是許多類型節(jié)點(diǎn)的組合,，其中相同類型的節(jié)點(diǎn)存在較多的連接，而不同類型節(jié)點(diǎn)的連接則相對(duì)較少,。把同一類型節(jié)點(diǎn)以及這些節(jié)點(diǎn)之間的邊所構(gòu)成的子圖稱為網(wǎng)絡(luò)中的社區(qū),。社區(qū)如圖1所示，圖中的小型網(wǎng)絡(luò)中包含3個(gè)社區(qū),，對(duì)應(yīng)圖中的3個(gè)橢圓,，在這些社區(qū)內(nèi)部，節(jié)點(diǎn)與節(jié)點(diǎn)之間的聯(lián)系非常緊密,，而社區(qū)之間的聯(lián)系則比較稀疏[2-4],。

    網(wǎng)絡(luò)社區(qū)發(fā)掘?qū)τ诹私饩W(wǎng)絡(luò)結(jié)構(gòu)和分析網(wǎng)絡(luò)特征具有重要的意義，目前已經(jīng)提出了具有基于節(jié)點(diǎn)集劃分的社區(qū)發(fā)現(xiàn)算法，例如基于貪婪算法原理的Kernighan-Lin算法,、基于譜思想的譜平分算法,、基于分裂思想的GN算法和基于凝聚思想的Newman快速算法等[5-7]。網(wǎng)絡(luò)社區(qū)發(fā)現(xiàn)的最終目的就是將網(wǎng)絡(luò)劃分為若干個(gè)互相獨(dú)立的社區(qū),，這些算法對(duì)研究社區(qū)發(fā)現(xiàn)都產(chǎn)生了重大的影響,。
1 算法設(shè)計(jì)
    由于網(wǎng)絡(luò)社區(qū)中節(jié)點(diǎn)之間的聯(lián)系相對(duì)緊密，社區(qū)之間節(jié)點(diǎn)的聯(lián)系相對(duì)稀疏,，根據(jù)這一特性,，本文提出了基于密度分布的社區(qū)發(fā)現(xiàn)算法。在實(shí)際網(wǎng)絡(luò)中,，存在一些節(jié)點(diǎn)與其他節(jié)點(diǎn)的聯(lián)系非常緊密,，即該節(jié)點(diǎn)的度最大，稱為“密度吸引點(diǎn)”,，其他節(jié)點(diǎn)以“密度吸引點(diǎn)”為中心,，從而形成社區(qū)。該算法的基本思想是以密度吸引點(diǎn)為初始社區(qū),，然后找出對(duì)該吸引點(diǎn)影響最大的節(jié)點(diǎn)依次加入到社區(qū),，一個(gè)網(wǎng)絡(luò)中存在可能不止一個(gè)吸引點(diǎn)，因此在網(wǎng)絡(luò)中可能存在多個(gè)社區(qū),，在計(jì)算節(jié)點(diǎn)影響度時(shí)要考慮對(duì)多個(gè)社區(qū)的影響,。直到所有的節(jié)點(diǎn)都被分到了各自的社區(qū)中。同時(shí)要考慮不同社區(qū)之間的影響度,，如果兩個(gè)社區(qū)之間的相互影響度非常大,，就認(rèn)為這兩個(gè)社區(qū)為一個(gè)社區(qū)，則合并這兩個(gè)社區(qū),。

1.2 算法描述
    本算法中,，假設(shè)社區(qū)內(nèi)部度數(shù)越大則社區(qū)密度越大；密度越大的社區(qū)對(duì)其周圍節(jié)點(diǎn)的吸引力越大,；對(duì)在同一個(gè)層次即相對(duì)密度吸引點(diǎn)來說密度相同的節(jié)點(diǎn)的吸引力相同,。
    (1)初始化網(wǎng)絡(luò)，將網(wǎng)絡(luò)中的每個(gè)節(jié)點(diǎn)看成是獨(dú)立的社區(qū),，計(jì)算社區(qū)的密度,，每個(gè)社區(qū)的初始密度為節(jié)點(diǎn)的度數(shù)；
    (2)找出網(wǎng)絡(luò)中密度最大的社區(qū),，該社區(qū)為密度吸引點(diǎn),；
    (3)根據(jù)影響函數(shù)，計(jì)算與密度吸引點(diǎn)相鄰社區(qū)對(duì)密度吸引點(diǎn)的影響度,，找出影響度最大的社區(qū),，此處認(rèn)為這個(gè)社區(qū)與密度吸引點(diǎn)為同一個(gè)社區(qū)（影響度最大的社區(qū)可能不止一個(gè)）,；
    (4)再次計(jì)算網(wǎng)絡(luò)中所有社區(qū)的密度，此時(shí)應(yīng)用密度函數(shù)進(jìn)行計(jì)算,，并找出密度最大的社區(qū)作為密度吸引點(diǎn),；
    (5)重復(fù)步驟(3)、步驟(4),，直到所有的社區(qū)都合并完成,，算法結(jié)束。
    算法流程圖如圖2所示,。

2 算法驗(yàn)證
    為了驗(yàn)證本算法的有效性,，將本算法應(yīng)用到Zachary′s Karate Club Network[9]和隨機(jī)的無標(biāo)度網(wǎng)絡(luò)。實(shí)驗(yàn)結(jié)果表明,，本算法可以將網(wǎng)絡(luò)劃分為大小不同的社區(qū),，且具有較好的效果。
2.1 Zachary′s Karate Club Network
    在復(fù)雜網(wǎng)絡(luò)社區(qū)結(jié)構(gòu)的研究中,，Zachary′s Karate Club Network是經(jīng)常被使用的經(jīng)典數(shù)據(jù)集,，它是20世紀(jì)70年代初期Zachary用了兩年的時(shí)間觀察得到的美國一所大學(xué)中空手道俱樂部成員的相互社會(huì)關(guān)系網(wǎng)絡(luò)。在這個(gè)網(wǎng)絡(luò)數(shù)據(jù)集中包含了34個(gè)節(jié)點(diǎn)和78條邊,，其中節(jié)點(diǎn)表示俱樂部成員,，邊表示成員之間的社會(huì)關(guān)系，網(wǎng)絡(luò)結(jié)構(gòu)如圖3所示,。
    通過應(yīng)用密度分布社區(qū)發(fā)現(xiàn)算法,，可以將該經(jīng)典網(wǎng)絡(luò)準(zhǔn)確地分為兩個(gè)社區(qū)，社區(qū)分布節(jié)點(diǎn)為：第一個(gè)社區(qū)(1,，2,，3，4,，5,，6，7,，8,，11，12,，13,，14，17,，18，20,，22),，第二個(gè)社區(qū)(9,，10，15,，16,，19，21,，23,，24，25,，26,，27，28,，29,，30，
31,，32,，33，34),。同時(shí)還發(fā)現(xiàn)由于網(wǎng)絡(luò)節(jié)點(diǎn)的分布遵循冪率分布定律,，因此社區(qū)合并的速度正好與冪率分布呈反比，即社區(qū)密度越小,，社區(qū)收斂的越快,。比較結(jié)果如圖4所示。

2.2 隨機(jī)無標(biāo)度網(wǎng)絡(luò)
    在現(xiàn)實(shí)網(wǎng)絡(luò)中,，大部分網(wǎng)絡(luò)都符合復(fù)雜網(wǎng)絡(luò)特性,，因此在第二個(gè)實(shí)驗(yàn)中，隨機(jī)截取了網(wǎng)絡(luò)中節(jié)點(diǎn)相互關(guān)聯(lián)的一部分隨機(jī)的無標(biāo)度網(wǎng)絡(luò)作為實(shí)驗(yàn)對(duì)象,，該網(wǎng)絡(luò)中共有62個(gè)節(jié)點(diǎn),，400條邊，節(jié)點(diǎn)代表其相應(yīng)的網(wǎng)頁,，邊代表網(wǎng)頁之間相互的連接關(guān)系,，其網(wǎng)絡(luò)結(jié)構(gòu)如圖5所示。
    在實(shí)驗(yàn)過程中,，對(duì)該網(wǎng)絡(luò)節(jié)點(diǎn)用1~62進(jìn)行了隨機(jī)的標(biāo)注,，通過應(yīng)用密度分布社區(qū)發(fā)現(xiàn)算法，成功地將社區(qū)分成了兩個(gè)部分,，社區(qū)收斂速度與冪率分布對(duì)比如圖6所示,。

    實(shí)驗(yàn)結(jié)果表明本算法可以準(zhǔn)確地將隨機(jī)無標(biāo)度網(wǎng)絡(luò)分為兩個(gè)社區(qū)，實(shí)驗(yàn)結(jié)果如圖7所示,。

    本文提出的基于密度分布的社區(qū)發(fā)現(xiàn)算法, 根據(jù)聚類算法中的密度分布函數(shù),，利用密度吸引點(diǎn),，通過計(jì)算影響函數(shù)，對(duì)網(wǎng)絡(luò)進(jìn)行聚類,，完成網(wǎng)絡(luò)社區(qū)的劃分,。利用兩個(gè)數(shù)據(jù)集對(duì)本算法進(jìn)行了有效性驗(yàn)證，結(jié)果表明,，該算法能準(zhǔn)確地找出網(wǎng)絡(luò)中存在的社區(qū),，并且發(fā)現(xiàn)社區(qū)收斂時(shí)與冪率分布的規(guī)律。本算法僅對(duì)部分社區(qū)進(jìn)行了實(shí)驗(yàn),，關(guān)于時(shí)間復(fù)雜度等并沒有進(jìn)行精確的計(jì)算,，以后還需要進(jìn)一步對(duì)該算法進(jìn)行驗(yàn)證和改進(jìn)。
參考文獻(xiàn)
[1] KERNIGHAN B W,，LIN S.An efficient heuristic procedure  for partitioning graphs[J].Bell System Technical Journal,，1970，49(2)：291-307.
[2] 馬興福,，王紅.一種新的重疊社區(qū)發(fā)現(xiàn)算法[J].計(jì)算機(jī)應(yīng)用研究,，2012，29(3)：844-846.
[3] 林友芳,，王天宇,，唐銳，等.一種有效的社會(huì)網(wǎng)絡(luò)社區(qū)發(fā)現(xiàn)模型和算法[J].計(jì)算機(jī)研究與發(fā)展,，2012,，49(2)：337-345.
[4] 李峻金，向陽,，牛鵬,，等.一種新的復(fù)雜網(wǎng)絡(luò)聚類算法[J]. 計(jì)算機(jī)應(yīng)用研究，2010,，27(6)：2097-2099.
[5] CAPOCCI A,，SERVEDIO V D P，CALDARELLI G,，et al.  Detecting communities in large networks[J].Physica A,，2005，352(2-4)：669-676.
[6] NEWMAN M E,，GIRVAN M.Finding and evaluating community structure in networks[J].Phys.Rev.E,，2004，69(2): 026113.
[7] DUCH J,，ARENAS A.Community detection in complex  networks using extreme optimization[J].Phys.Rev.E,，2005，72(2)：027104.
[8] 韓家煒,，坎伯.數(shù)據(jù)挖掘概念與技術(shù)[M].范明,，孟小峰,，譯. 北京：機(jī)械工業(yè)出版社,，2001.
[9] 汪小帆,，李翔，陳關(guān)榮.復(fù)雜網(wǎng)絡(luò)及其應(yīng)用[M].北京：清華大學(xué)出版社,，2006.