工程中的信號(hào)一般較微弱,，很容易被噪聲污染，如何有效地進(jìn)行檢測(cè)是信號(hào)處理領(lǐng)域的首要問題,。混沌振子是產(chǎn)生混沌現(xiàn)象的一種非線性系統(tǒng),，許多文獻(xiàn)已經(jīng)證實(shí)它對(duì)周期信號(hào)具有較強(qiáng)敏感性并對(duì)噪聲具有一定免疫性[1-2]，現(xiàn)已被廣泛應(yīng)用到工程中微弱周期信號(hào)檢測(cè)領(lǐng)域,，如生物醫(yī)學(xué)信號(hào)檢測(cè),、軍事雷電信號(hào)探測(cè)、地震信號(hào)遠(yuǎn)程檢測(cè),、工業(yè)機(jī)械故障診斷等,。然而，混沌振子用于周期信號(hào)的檢測(cè)還存在需進(jìn)一步完善的問題,，如噪聲對(duì)相變的影響程度什么情況下可以忽略,；初值和相位差影響的問題等。
　本文通過實(shí)驗(yàn)觀察噪聲對(duì)輸出量的影響,，闡述了噪聲對(duì)混沌振子檢測(cè)信號(hào)影響程度的大小,，提出了基于集合經(jīng)驗(yàn)?zāi)Ｊ椒纸?/a>(EEMD)的降噪方法；針對(duì)相位差影響問題,，通過理論計(jì)算檢測(cè)相位角范圍,，得出正反導(dǎo)入法最簡(jiǎn)單的解決方法，最后通過對(duì)仿真信號(hào)檢測(cè),，給出混沌振子結(jié)合EEMD降噪對(duì)信號(hào)進(jìn)行檢測(cè)的方法和步驟,，并驗(yàn)證了方法的有效性。

    由于非線性項(xiàng)的存在,，Holmes型混沌振子方程表現(xiàn)出豐富的動(dòng)力學(xué)特性,。相軌跡隨F有規(guī)律地發(fā)生相變，使得混沌振子方程檢測(cè)周期信號(hào)成為可能。設(shè)置F為相變臨界值,，將待測(cè)信號(hào)加載到式(1)右邊,，若加載前后發(fā)生相變，據(jù)此判斷待測(cè)信號(hào)含有與周期策動(dòng)力同頻的分量,，達(dá)到檢測(cè)周期信號(hào)的目的,。

   由式(5)可以得出結(jié)論：噪聲引起的混沌系統(tǒng)輸出的改變量方差與噪聲方差和計(jì)算步長(zhǎng)成正比。當(dāng)噪聲強(qiáng)度或計(jì)算步長(zhǎng)太大時(shí),，會(huì)對(duì)系統(tǒng)的輸出和相圖產(chǎn)生一定的影響,，所以需要先對(duì)含強(qiáng)噪聲的信號(hào)進(jìn)行降噪，再用混沌振子方程進(jìn)行檢測(cè),。
3 基于EEMD的信號(hào)降噪方法
    EEMD是由Huang等人于2008年提出的一種處理平穩(wěn)及非平穩(wěn)信號(hào)的新方法,，它將信號(hào)分解為多個(gè)固有模式函數(shù)分量IMF(Intrinsic Mode Function)，這些IMF的頻率由高到低依次分布,，具有很強(qiáng)的頻率選層性能,，是一種完全自適應(yīng)的分解方法，并且能克服模式混疊現(xiàn)象,、端點(diǎn)效應(yīng)等問題[5],。關(guān)于EEMD的分解原理及步驟，參考文獻(xiàn)[4]給出了詳細(xì)的闡述,，這里不再說明,。
    用EEMD實(shí)現(xiàn)降噪的步驟[6-7]如下：

　將降噪后的信號(hào)再次導(dǎo)入到混沌振子式(1)的右邊，得到其輸出信號(hào)波形和相軌跡如圖3所示,。由此看出,，先用EEMD抑制強(qiáng)噪聲，再用混沌振子檢測(cè)能有效克服噪聲的影響,。

5.2 故障軸承振動(dòng)信號(hào)的檢測(cè)
   用混沌振子檢測(cè)某故障軸承的振動(dòng)信號(hào),。已知故障軸承型號(hào)為N205EM，外徑為52 mm,、內(nèi)徑為25 mm,、滾動(dòng)體數(shù)12、滾動(dòng)體直徑為7.5 mm,、接觸角為0°,。將該軸承放在旋轉(zhuǎn)機(jī)械振動(dòng)故障試驗(yàn)平臺(tái)上做測(cè)試，設(shè)置轉(zhuǎn)速為600 r/min,，采樣頻率為20 kHz,，采集其振動(dòng)信號(hào)時(shí)域波形如圖4所示。由圖看出此軸承的振動(dòng)信號(hào)含有較強(qiáng)的噪聲,對(duì)其用EEMD方法進(jìn)行降噪處理,，降噪后波形如圖5所示,。

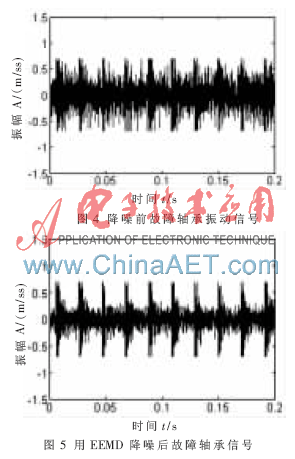
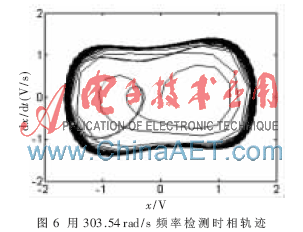
    理論上可以計(jì)算出該故障軸承的各特征頻率[10],。建立三個(gè)混沌檢測(cè)方程，設(shè)置對(duì)應(yīng)的頻率值,，調(diào)整對(duì)應(yīng)的相變閾值和計(jì)算步長(zhǎng),，使其相軌跡處于混沌態(tài)與大尺度周期態(tài)的臨界，對(duì)應(yīng)的數(shù)據(jù)如表2所示,。將降噪后的故障軸承信號(hào)導(dǎo)入到三個(gè)檢測(cè)方程中,，ω=303.54的檢測(cè)結(jié)果如圖6所示?？梢钥闯?，此時(shí)混沌振子的相軌跡進(jìn)入大尺度周期狀態(tài)，而其余的相軌跡仍處于混沌狀態(tài),，由此可以判斷軸承的振動(dòng)信號(hào)含有頻率為48.31 Hz的周期成分,，進(jìn)而判斷軸承外環(huán)故障，這與軸承的實(shí)際故障情況一致,。

    通過實(shí)驗(yàn)觀察說明混沌振子對(duì)噪聲的免疫力是相對(duì)的,，理論推導(dǎo)出噪聲對(duì)輸出的影響量噪聲方差和計(jì)算步長(zhǎng)成正比,。因此用混沌振子檢測(cè)信號(hào)時(shí),，不能忽視強(qiáng)噪聲對(duì)檢測(cè)結(jié)果的影響。
    提出了基于EEMD的信號(hào)降噪方法,，將其與混沌振子結(jié)合起來檢測(cè)周期信號(hào),，并采用正反導(dǎo)入法克服相位差對(duì)檢測(cè)的影響。對(duì)仿真信號(hào)和故障軸承振動(dòng)的檢測(cè)效果驗(yàn)證了該方法的有效性,。
參考文獻(xiàn)
[1] Liu Xuanchao. Weak signal detection research based on doffing oscillator used for downhole communication[J]. Journal of Computers., 2011,6(2):359-367.
[2] 陳偉,黃芮,林師善,等. 基于Launchpad微弱信號(hào)檢測(cè)裝置的研究[J].電子技術(shù)應(yīng)用, 2013,39(9):47-49.
[3] 李月,楊寶俊.檢測(cè)強(qiáng)噪聲背景下周期信號(hào)的混沌系統(tǒng)[J]. 科學(xué)通報(bào),2003,48(1):19-20.
[4] Su Liyun,Yang Qian, Zhang Yuli. Noise immunity of duffing oscillator and its applications in weak UWB signal detection [J]. Journal of Networks, 2012,7(3):540-546.
[5] WU Z H, HUANG N E. Ensemble empirical mode decomposition: a noise assisted data analysis method[J]. Advance in Adaptive Data Analysis, 2009,1(1):1-41.
[6] 王婷.EMD算法研究及其在信號(hào)去噪中的應(yīng)用[D].哈爾濱：哈爾濱工程大學(xué),，2010.
[7] YEH J R, SHIEH J S. Complementary ensemble empirical  mode decomposition: A noise enhanced data analysis method[J]. Advances in Adaptive Data Analysis, 2010,2(2):135-155.
[8] 李樹鈺.改進(jìn)的小波閾值去噪方法及其在MATLAB中的仿真[J]. 噪聲與振動(dòng)控制, 2010,4(2):121-124.
[9] 賴志慧，冷永剛,，孫建橋,等.基于Duffing振子的變尺度微弱特征信號(hào)的檢測(cè)方法研究[J]. 物理學(xué)報(bào),2012,61(5):50-53.
[10] 李強(qiáng). 機(jī)械設(shè)備早期故障預(yù)示中的微弱信號(hào)檢測(cè)技術(shù)研究[D].天津：天津大學(xué), 2008.