《電子技術(shù)應(yīng)用》
您所在的位置：首頁 > 嵌入式技術(shù) > 設(shè)計應(yīng)用 > 一種CABG手術(shù)輔助機器人運動補償方法研究
一種CABG手術(shù)輔助機器人運動補償方法研究
2014年電子技術(shù)應(yīng)用第6期
梁 帆， 崔世鋼,， 趙 麗,， 吳興利， 楊莉莉
天津職業(yè)技術(shù)師范大學(xué) 天津市信息傳感與智能控制重點實驗室, 天津 300222
摘要： 針對非體外循環(huán)心臟動脈旁路移植手術(shù)中輔助機器人的運動控制問題,，提出基于多測量耦合模型的多步預(yù)測控制算法,，該算法增加了加速度測量并采用卡爾曼濾波器作為狀態(tài)觀測器進行信息融合處理，增強了對機器人運動狀態(tài)的估計,，進而提高心臟運動信號的跟蹤性能,。同時超前的N步預(yù)測增加了系統(tǒng)的帶寬。實驗結(jié)果表明,，使用了耦合模型的多傳感器信息融合多步預(yù)測控制算法的機器人系統(tǒng)將跟蹤相對運動誤差減小了20%,。
中圖分類號： TP242.6
文獻標(biāo)識碼： A
文章編號： 0258-7998(2014)06-0074-04
Motion compensation of the CABG surgery assisted robot
Liang Fan，Cui Shigang,， Zhao Li,， Wu Xingli， Yang Lili
Tianjin Key Laboratory of Information Sensing & Intelligent Control, Tianjin University of Technology and Education, Tianjin 300222, China
Abstract： Aimming at the motion control of assisted robot in the off pump Coronary Artery Bypass Graft（CABG）surgery, we propose a coupled model based multi-sensor fused N step predictive control algorithm in this paper. The method takes Kalman filter as its state observer to improve the state estimation and thus enhance the tracking performance. Furthermore, The N step predictions enlarge the system bandwidth. The comparison experiment results shows that tracking error from the coupled model based model predictive control algorithm are 20% less than that using position only model.
Key words : tracking control; surgical assisted robotics; model predictive control; heart motion prediction; coupled model; extended Kalman filter

       冠心病是人類主要的致死疾病之一,。冠心病的手術(shù)治療方法是體外循環(huán)冠狀動脈旁路移植手術(shù),，但是手術(shù)中心臟停跳會給病人帶來術(shù)后并發(fā)癥[1]，不僅增加了醫(yī)療成本而且大大延長了病人術(shù)后恢復(fù)的時間,。為了解決這一問題,，醫(yī)生希望采用非體外循環(huán)的方法，即在手術(shù)過程中采用使心臟始終保持在完全跳動狀態(tài)(區(qū)別于使用機械靜止器的非完全跳動的情況)的手術(shù)方式完成操作,。由于心臟運動信號運動快,、幅度大，醫(yī)生無法手工跟蹤心臟運動來完成手術(shù)[2],。如今隨著機器人技術(shù)的發(fā)展,，機器手臂可以幫助醫(yī)生跟蹤心臟運動來完成心臟不停跳的非體外循環(huán)旁路移植手術(shù)。其工作是消除機器人手術(shù)工具端點與心臟表面某操作點的相對運動,，使得機器人與心臟保持相對靜止,。醫(yī)生在此基礎(chǔ)上，通過操作手柄疊加運動完成遠程遙控手術(shù)操作,。在這里只考慮運動跟蹤問題,，疊加運動作為以后研究的內(nèi)容。

        在心臟旁路移植手術(shù)中,，冠狀動脈血管的直徑范圍為0.5~2.0 mm,。為了保證手術(shù)安全，動態(tài)誤差應(yīng)保持在血管直徑的1%以內(nèi),，即對于高頻帶心臟運動的動態(tài)跟蹤誤差要保持在小于100 μm的范圍內(nèi),。在以往的研究中，NAKAMURA Y[3]等人使用了反饋控制方法,；OORTMAIER T[4]等人提出基于Taken原理心臟運動預(yù)測方法的控制方法,；GINHOUX R[5]等人提出廣義模型預(yù)測控制器；DUINDAM V和SASTRY S[6]提出基于模型的漸進控制算法,。參考文獻[7]提出心臟運動信號的自適應(yīng)時變線性回歸模型,，將心臟信號跟蹤問題轉(zhuǎn)化為基于心臟運動信號模型的運動跟隨問題，并應(yīng)用最優(yōu)跟蹤理論,，實現(xiàn)了基于心臟運動模型的隨動跟蹤控制,。以往的研究結(jié)果表明,基于模型的預(yù)測控制算法是解決心臟手術(shù)輔助機器人跟蹤控制問題的有效方法，其優(yōu)點是對心臟未來運動的預(yù)測增加了系統(tǒng)的帶寬,，讓控制器超前對心臟運動的位置做出判斷進而準(zhǔn)確跟蹤,。

        本文提出了一種基于位置與加速度信號的耦合模型的多步模型預(yù)測控制方法。該方法的優(yōu)勢表現(xiàn)在：(1)增加了對機器人端點的3D加速度測量,，因為加速度是位移的二階導(dǎo)數(shù),，所以在一定程度上擴大了加速度的測量系統(tǒng)的帶寬；多傳感測量信息經(jīng)過卡爾曼濾波器的融合處理為控制器提供了更多的超前運動信息,。(2)心臟運動時變模型提供超前并非單步的,，而是N步的參考輸入，這樣的做法同樣擴大了系統(tǒng)的帶寬,。

1 手術(shù)輔助機器人耦合模型

        圖1是PHANToM實驗平臺的坐標(biāo)系統(tǒng)和初始位置示意圖,。其中小寫的x-y-z代表基準(zhǔn)空間坐標(biāo)系，大寫的X-Y-Z代表工作空間的坐標(biāo)系,為了計算方便選取兩者重合,。

        機器人系統(tǒng)的動態(tài)模型用質(zhì)量-彈簧-阻尼物理系統(tǒng)來近似,，因為機器人實驗平臺端點可以在3D空間中自由運動，因此可以得到3個彼此獨立并且結(jié)構(gòu)相近的物理模型,。在此首先要研究一下3D機器人實驗平臺在笛卡爾坐標(biāo)系下的X軸運動方向上的狀態(tài)變量,。圖2展示了帶有加速度測量與位置測量的PHANToM實驗平臺的x軸質(zhì)量-阻尼-彈簧近似物理模型[8]。

        選擇狀態(tài)變量：

        

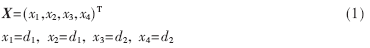
其中d1是M1的位移,，d2是M2的位移,，因此模型的狀態(tài)空間表達為:

        

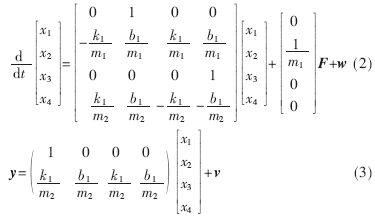
其中b1為扭轉(zhuǎn)粘性摩擦參數(shù),k1為彈簧系數(shù),F為施加在m1的外部作用力,w為過程噪聲向量,v為測量噪聲向量。通過式(3)可以看出m的加速度是狀態(tài)變量的線性組合,。其優(yōu)勢在于當(dāng)?shù)玫搅思铀俣葴y量值,，將加速度測量值和位置測量值用來作狀態(tài)估計比單獨的位置測量值能夠?qū)ο到y(tǒng)狀態(tài)提供更有效的估計，進而提高機器人動態(tài)跟蹤性能,。由式(2),、式(3)位移-轉(zhuǎn)矩和加速度-轉(zhuǎn)矩的傳遞函數(shù)分別由式(4)、式(5)所示：

        

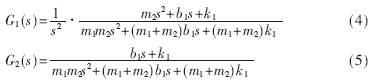
        以上兩個帶參數(shù)模型有部分相同的參數(shù),，是兩個相互耦合的模型,。當(dāng)?shù)玫捷斎胼敵鰯?shù)據(jù)的離散傅里葉變換后,，便可以利用非線性最優(yōu)化的方法來確定兩個傳遞函數(shù)的參數(shù)。

2 手術(shù)輔助機器人的控制算法

        控制算法是整個手術(shù)輔助機器人跟蹤控制的核心,。心臟表面的手術(shù)操作點的運動幅度高達12 mm,，最高運動頻率高達26 Hz?；谛呐K運動信號的分析,，心臟表面某點存在兩種運動模式，分別是1 Hz以下的呼吸運動主導(dǎo)的運動及2 Hz心臟運動主導(dǎo)的心跳運動,。呼吸運動的跟蹤僅僅可以通過反饋控制器來完成,，而心跳運動則要通過前饋控制器來超前消除。前饋控制器需要知道心臟運動值的超前信息來相應(yīng)地做出補償,，因此應(yīng)用模型預(yù)測控制首先要得到心臟運動的N步預(yù)測值,，將其作為模型預(yù)測控制器的參考輸入，基于耦合模型的預(yù)測控制器得到位置與加速度測量值,，運算得到的機器人輸出控制率的前饋部分和反饋部分便分別滿足對心臟運動兩個主導(dǎo)模式的跟蹤控制,。

2.1 基于心臟運動時變模型的N步預(yù)測

        參數(shù)時變模型來模擬心臟運動表示為：只受過程白噪聲干擾的隨機漫步過程。定義測量值h(t)=y(t),，時變參數(shù)傅里葉級數(shù)模型的狀態(tài)空間表示為：

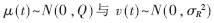分別為模型噪聲與測量噪聲,。噪聲默認(rèn)為白噪聲。對于心臟未來運動信號的預(yù)測需要通過估計模型中的狀態(tài)來解決,?？紤]到測量方程為非線性方程，擴展卡爾曼濾波器可以用來估計時變的狀態(tài)參數(shù),。首先將非線性的測量方程在當(dāng)前的狀態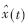(tài)點線性化得到測量矩陣C：

        

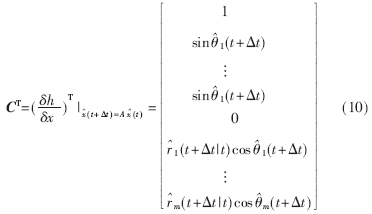
        接著按照卡爾曼濾波的遞推方程估計下一個時間的狀態(tài),。遞推方程表述為：

        

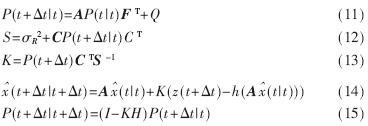
其中P為狀態(tài)估計均方值。利用上述遞推方程便可得到模型預(yù)測控制所需的心臟運動N步超前預(yù)測值：

        

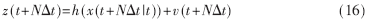
2.2 基于耦合模型的機器人模型預(yù)測控制算法

        模型預(yù)測控制的原理框圖如圖3表示,。與傳統(tǒng)預(yù)測控制的不同之處是將狀態(tài)觀測器改進為基于耦合模型的卡爾曼濾波器來對機器人運動狀態(tài)的估計,。同時保留前饋通路的控制率輸出。在應(yīng)用卡爾曼濾波器作狀態(tài)估計的過程中,，卡爾曼濾波器會考慮耦合模型的過程誤差和傳感器的測量誤差模型作為設(shè)計參數(shù)包含于整個算法之中,。這樣得到狀態(tài)估計優(yōu)于一般的狀態(tài)觀測器。因此,，基于耦合模型的預(yù)測控制問題可以描述為：已知未來N步參考輸入值,，應(yīng)用最優(yōu)化的方法求解目標(biāo)方程，其中機器人耦合模型作為目標(biāo)方程的約束條件,，求解出未來N步控制率輸出,，僅選取當(dāng)前點傳送給機器人。以下為推導(dǎo)過程。

        機器人耦合動態(tài)模型為：

        

        這里定義N步預(yù)測值為向量yest[k],，k0<k<k0+T指在時間k0與k0+T之間的采樣時間,。機器人的位置輸出逼近信號yest[k]，則最優(yōu)控制目標(biāo)方程為：

        改進的預(yù)測控制中,，式(27)中的x[k]由卡爾曼濾波器的輸出替代,。每個控制周期中，心臟運動時變信號模型提供超前N步的心臟運動估計值傳遞給控制器作為參考值,，控制器跟蹤參考值按照上述公式計算出前饋與反饋輸出率,。

3 實驗和結(jié)果

3.1 實驗平臺

        控制算法通過實驗平臺PHANToM Premium 1.5A實現(xiàn),。3D加速度傳感器使用是Freescale MMA7340L,。在實驗設(shè)置中，控制算法運行在2.6 GHz Intel Pentium4 PC 上Matlab xPC Target v2.8實時內(nèi)核中,。計算機控制系統(tǒng)的采樣頻率為0.5 ms,。在每次試驗前，先校準(zhǔn)機器人,。機器人的端點從系統(tǒng)初始位置開始跟蹤信號,。在實驗中，預(yù)先采集的心臟信號用于模擬實際的非體外循環(huán)手術(shù)中心臟在每個采樣時刻跳動位置的數(shù)值,。

3.2 實驗結(jié)果及討論

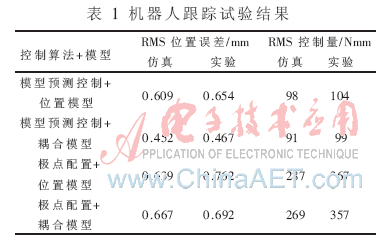
        實驗對比了模型預(yù)測控制器與極點配置控制器分別在單獨位置測量模型與耦合模型的情況下對心臟的運動跟蹤,。通過對算法結(jié)果比較得出基于耦合模型的多步預(yù)測控制算法在兩方面優(yōu)于其他控制算法：(1)增加加速度測量的耦合模型預(yù)測控制增加了系統(tǒng)帶寬，對所跟蹤的信號具有超前補償能力,。(2)多步預(yù)測增強了基于耦合模型的多步預(yù)測控制算法對于心跳信號快速變化的估計與跟蹤能力,，進而提高控制精度。表1總結(jié)了實驗得到的RMS跟蹤誤差與RMS控制量輸出,。圖4展示了在耦合模型與單獨位置模型的預(yù)測控制算法下,，機器人端點工作空間坐標(biāo)系中X軸位置、跟蹤誤差與控制量輸出,。圖中分別用不同的時間尺度表現(xiàn)兩個模型對應(yīng)的算法的優(yōu)劣,。

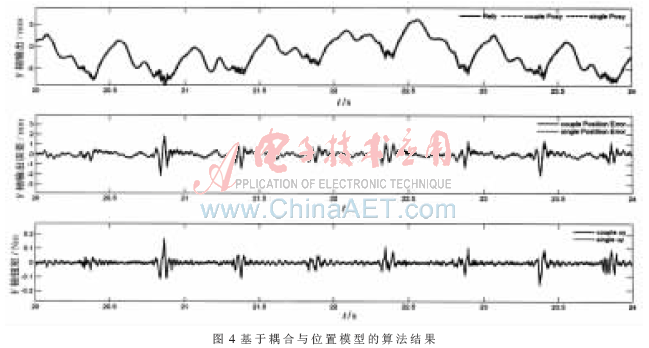
        本文中提出了基于速度與加速度測量的耦合模型的改進預(yù)測控制算法。在耦合模型的算法結(jié)構(gòu)下,，通過增加加速度傳感器對機器人端點運動的測量提高了跟蹤精度,。模型預(yù)測控制器按照心臟運動信號的特點分別對心臟運動中高頻與低頻分量分離出前饋控制率與反饋控制率，前饋部分的引入克服了測量在反饋環(huán)節(jié)產(chǎn)生滯后性,。

        本文結(jié)論如下：(1)模型預(yù)測控制算法具有超前預(yù)測的屬性,。將信號跟蹤問題歸結(jié)為參考信號預(yù)測問題，是算法前饋控制部分的必要基礎(chǔ),。通過提高模型預(yù)測的精度實現(xiàn)提高跟蹤控制的精度,，為高帶寬高精度的信號跟蹤提供了可能。(2)包含了加速度信號測量信息的耦合模型,，具備由于僅位置測量的超前相位的特征,，提高了機器人對高帶寬信號的準(zhǔn)確跟蹤能力,。試驗結(jié)果表明本文提出的帶有加速度測量耦合模型跟蹤算法比現(xiàn)有的位置測量算法的跟蹤誤差減小至少20%。

參考文獻

[1] NEWMAN M F,KIRCHNER J L,PHILLIPS-BUTE B,et al.Longitudinal assessment of neurocognitive function after coronary-artery bypass surgery [J]. New England J Med.,2001,6(344):395-402.

[2] FALK V. Manual control and tracking-A human factr analysis relevant for beating heart sugery[J].Thoracic Surg,2002,74:624-628.

[3] NAKAMURA Y, KISHI K,KAWAKAMI H. Heartbeat synchronization for robotic cardiac surgery[C]. in Proc.of IEEE International Conference on Robotics and Automation(ICRA),Seoul, Korea, May 2001,2. 2014-2019.

[4] ORTMAIER T, GROGER M, BOEHM D H, et al. Motion estimation in beating heart surgery[J]. IEEE Transactions on Biomedical Engineering, October 2005,52(10):1729-1740.

[5] GINHOUX R, GANGLOFF J A, DEMATHELIN M F,et al.Active filtering of physiological motion in robotized surgery using predictive control[J]. IEEE Transactions on Robotics, 2005,21(1):67-79.

[6] DUINDAM V, SASTRY S. Motion estimation and control for roboticassisted beating-heart surgery[C]. in Proc.of  IEEE/RSJ International Conference on Intelligent Robots  and Systems,San Diego,CA,USA,October-November 2007:871-876.

[7] 梁帆,，孟曉風(fēng),，董登峰.心臟動脈旁路手術(shù)中手術(shù)輔助機器人的模型跟隨控制[J]. 光學(xué)精密工程, 2012,20(1): 131-139

[8] MURAT CENK CAVUSOGLU DAVID FEYGIN and FRANK TENDICK. A Critical Study of the Mechanical and Electrical Properties of the PHANToM Haptic Interface and Improvements for High-Performance Control[J]. 2002,11(6): 555-568.

[9] ANDERSON B D, MOORE J B. Optimal control linear quadratic methods[M]. Englewood Cliffs, NJ: Prentice-Hall,1990.

此內(nèi)容為AET網(wǎng)站原創(chuàng)，未經(jīng)授權(quán)禁止轉(zhuǎn)載,。