早在1893年,，美國科學(xué)家TESLA N利用無線電能傳輸原理，在沒有任何導(dǎo)線相連接的情況下點亮了磷光照明燈^[1],，這是人類在無線能量傳輸初期的重要嘗試，同時也為人類向無線能量傳輸方向的發(fā)展提供了借鑒意義,。一個多世紀(jì)以來國內(nèi)外的學(xué)者對該技術(shù)進(jìn)行長期,、大量的研究,，在近距離和遠(yuǎn)距離無線電能傳輸理論和應(yīng)用層次上已經(jīng)取得了很大的進(jìn)展，但是在中等距離(傳輸距離一般為傳輸線圈直徑的幾倍)的傳輸范圍一直沒有突破性進(jìn)展,。直到2007年，MIT的SOLJACIC M教授領(lǐng)導(dǎo)的小組利用電磁諧振原理,，成功地在實驗室實現(xiàn)了近場內(nèi)電能的中距離無線傳輸^[2],。該技術(shù)的提出為中程距離無線電能傳輸技術(shù)的發(fā)展開辟了一個嶄新的方向,。

        目前,，諧振式無線能量傳輸已成為學(xué)術(shù)界和產(chǎn)業(yè)界共同關(guān)注的熱點。在實際應(yīng)用中,，隨著用電設(shè)備的種類和數(shù)量的增加,，特別是移動電子產(chǎn)品的不斷增加，利用單一電源給多個負(fù)載進(jìn)行無線充電具有廣闊的市場前景,。參考文獻(xiàn)[3]研究了多個接收線圈的情況,，但忽略了線圈間的電感交叉耦合影響。而多接收線圈的引入會帶來一些新的問題,，如接收線圈之間的交叉耦合效應(yīng)會擾動系統(tǒng)的工作狀態(tài)，結(jié)果不但使系統(tǒng)的分析和設(shè)計復(fù)雜化,，還會影響系統(tǒng)在諧振頻率點處的傳輸效率與傳輸功率,。因此有必要采取方法來補(bǔ)償交叉耦合的影響。

        為此,，本文從單電源,、雙負(fù)載無線充電系統(tǒng)的等效電路模型出發(fā)，詳細(xì)研究和分析了三諧振線圈系統(tǒng)的交叉耦合對各線圈電流和系統(tǒng)的傳輸功率,、效率的影響,。在此基礎(chǔ)上，提出了一種在回路中附加電抗來補(bǔ)償交叉耦合效應(yīng)的方法,，并通過仿真與實驗證明了這種補(bǔ)償?shù)目尚行院陀行浴?/p>

1 理論分析

1.1 集總參數(shù)的等效電路模型

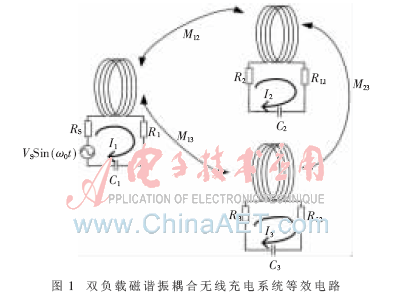
        圖1所示為兩個負(fù)載線圈的磁諧振耦合無線充電系統(tǒng)等效電路,。R_S,、R_L1、R_L2為電源等效內(nèi)阻以及兩負(fù)載電阻,，R₁,、R₂、R₃是各回路的損耗電阻,，包括線圈和電容上的耗散電阻,；M₁₂、M₁₃,、M₂₃分別為兩兩線圈之間的互感,；L₁,、L₂,、L₃與C₁、C₂,、C₃分別為源端和接收端的電感和調(diào)諧電容,，并且滿足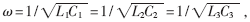ω與驅(qū)動源的角頻率一致。

        根據(jù)基爾霍夫定律,，可得描述電路的方程：

其中I=[I₁  I₂  I₃]^T,，I₁、I₂,、I₃分別為3個耦合線圈上的電流,，V=[V_S  0  0]^T為電壓列向量。當(dāng)系統(tǒng)發(fā)生諧振時,，即系統(tǒng)工作在諧振頻率點ω₀時,，滿足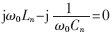(n=1，2,，3),。Z為電路的阻抗矩陣，如式(2)所示：

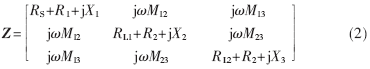
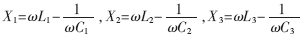        分別為發(fā)射端,、接收負(fù)載1和接收負(fù)載2端的電抗,。電感耦合系數(shù)：

其中k₂₃是兩接收線圈間的交叉耦合系數(shù)。兩負(fù)載所獲得的平均傳輸功率定義為：

1.2 無交叉耦合時系統(tǒng)的最佳工作狀態(tài)

        為了控制兩接收線圈的功率分配比,，除了可以調(diào)節(jié)兩接收線圈與發(fā)射線圈間的距離比之外,，還能通過調(diào)整線圈間的負(fù)載阻抗比來完成。由參考文獻(xiàn)[4]可知,，兩負(fù)載端在源端的等效阻抗分別為：

        當(dāng)電源內(nèi)阻抗和負(fù)載等效阻抗共軛匹配時,，負(fù)載能獲得最大的傳輸功率，因此負(fù)載獲得最大功率的條件是：

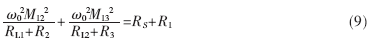
1.3 交叉耦合的影響

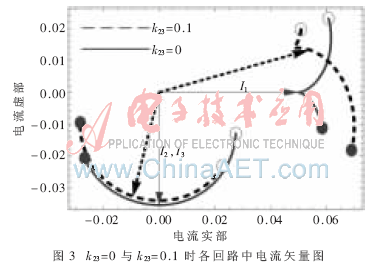
        上文中忽略了交叉耦合效應(yīng),，然而在實際的電路中,，交叉耦合系數(shù)往往并不為零,，而兩負(fù)載之間的交叉耦合有可能影響甚至惡化系統(tǒng)整體的傳輸性能。為方便分析,，本文僅僅考慮收發(fā)線圈在同軸且兩負(fù)載線圈鏡像的情況,。根據(jù)式(1)～式(5)，利用數(shù)值方法,，給出了考慮交叉耦合和不考慮交叉耦合情況下系統(tǒng)的傳輸功率及傳輸效率數(shù)值解和三線圈各回路的電流矢量圖,。計算中取R_L1=R_L2=R_S=50 Ω，R₁=R₂=R₂=1 Ω,，f=4.6 MHz,，將以上取值代入式(9)求得系統(tǒng)處于最佳工作狀態(tài)時的耦合系數(shù)為k₁₂=k₁₃=0.122，此時由諾依曼公式可以算出兩負(fù)載線圈之間的交叉耦合系數(shù)k₂₃約為0.1,，并與k₂₃=0時系統(tǒng)的傳輸功率、傳輸效率以及三線圈電流矢量圖進(jìn)行對比,，如圖2和圖3所示,。

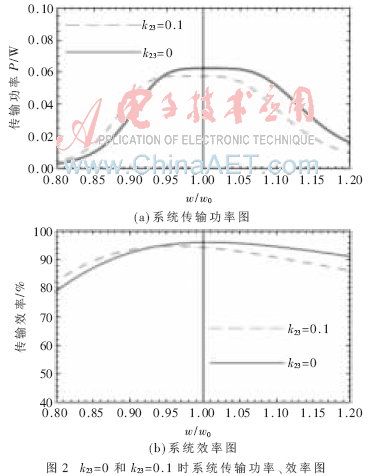
        由圖2可知，若k₂₃=0,，則系統(tǒng)的輸出功率和效率極值點均在諧振頻率點ω₀處,；若k₂₃=0.1，則不僅會造成系統(tǒng)傳輸功率極值點產(chǎn)生漂移,，還會導(dǎo)致系統(tǒng)在諧振頻率ω₀處傳輸功率和效率的降低,。

        圖3中給出了k₂₃=0和k₂₃=0.1兩種情況下三線圈中的電流矢量圖。圖中空心圓圈,、實心圓圈和箭頭分別代表ω/ω₀=0.92,、1.08和1時的電流矢量。若不考慮交叉耦合效應(yīng),，在諧振頻率ω₀處,，發(fā)射線圈的電流與電源電壓同相，兩個接收線圈上的電流相位和幅值都相同,，且比發(fā)射線圈滯后90°,。若考慮交叉耦合效應(yīng)，在諧振頻率ω₀處,，發(fā)射線圈電流與電源電壓不再同相,，兩負(fù)載線圈電流滯后發(fā)射線圈大于90°，且電流I₂,、I₃幅值略有減小,。

1.4 電抗補(bǔ)償原理

        為了克服交叉耦合對系統(tǒng)傳輸性能的不利影響，本文提出一種利用附加電抗來彌補(bǔ)交叉耦合效應(yīng)的方法——電抗補(bǔ)償法,。其原理如圖4所示,，為補(bǔ)償非相鄰線圈的交叉耦合效應(yīng)而附加的電抗元件(電感或電容),。

        在各回路串聯(lián)了補(bǔ)償電抗后，希望在諧振角頻率ω₀處,，各回路電流的相位和幅值大小與忽略交叉耦合時一致,。為此，分別寫出ω=ω₀并考慮交叉耦合且有補(bǔ)償電抗和忽略交叉耦合但無補(bǔ)償電抗時的電流回路方程,，如式(10),、式(11)所示。因為兩系統(tǒng)工作在諧振頻率點ω₀時,，均滿足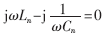(n=1,，2，3),即有X₁=X₂=X₃=0,。

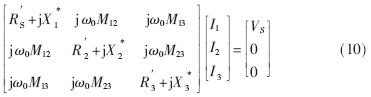
        采用與1.3節(jié)相同的數(shù)據(jù)R_L1=R_L2=R_S=50 Ω,，R₁=R₂=R₃=1 Ω，f=4.6 MHz,，計算得到補(bǔ)償電抗29 Ω,。用數(shù)值計算方法仿真以上兩系統(tǒng)補(bǔ)償前后的電流幅值圖，如圖5所示,。

        圖5中,，空心圓圈、實心圓圈和箭頭分別代表ω/ω₀=0.92,、1.08和1時的電流矢量,。可以看出,，電抗補(bǔ)償后各回路的電流矢量圖與無交叉耦合時的電流矢量圖恰好完全重合,，即補(bǔ)償前后三線圈電流的幅值大小相等、相位相同,，表明回路中加入補(bǔ)償電抗后能徹底抵消交叉耦合帶來的影響,，從而也說明了這種補(bǔ)償方法的理論可行性。

2 補(bǔ)償電抗的實現(xiàn)

        前面討論中使用的補(bǔ)償電抗是頻率無關(guān)器件,，現(xiàn)實中可用電感或者電容來實現(xiàn),。雖然電感或電容的電抗值與頻率有關(guān)，但考慮到諧振式無線能量傳輸系統(tǒng)是窄帶工作的,，因此影響不大,。

        假設(shè)補(bǔ)償電抗(即分別用電感來補(bǔ)償系統(tǒng))時，三回路的電抗部分均可以寫成如下形式：        

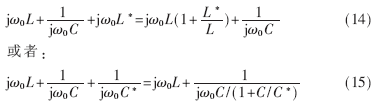
式(14)表示原來的回路電感應(yīng)修正為,，即給原有的線圈串聯(lián)一個電感量為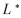的電感,。對于磁諧振耦合無線能量傳輸系統(tǒng)，回路中補(bǔ)償電感的引入有可能會明顯擾動系統(tǒng)原有的磁場的分布,，從而影響線圈原有的耦合狀態(tài),。為避免這一不利影響,，本文采用電容補(bǔ)償方式。

        當(dāng)采用電容補(bǔ)償時,，根據(jù)式(15),，只需將原回路可調(diào)電容調(diào)整為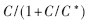即可達(dá)到目的。

3 數(shù)值仿真與實驗結(jié)果

        實驗中用到的測試平臺為EE1640C系列函數(shù)信號發(fā)生器和GDS-2202數(shù)字存儲示波器,。實驗中用到的3個線圈都是由線徑1.5 mm的漆包銅線繞制5圈而成,，線圈直徑16 cm,電感值約為10 μH,可調(diào)諧電容為120 pF，工作頻率為4.6 MHz,，三線圈依次按照接收線圈1,、發(fā)射線圈、接收線圈2的順序同軸等間距放置,，相鄰線圈之間距離為5 cm,，則兩負(fù)載線圈之間的距離為10 cm，由諾依曼公式可以算出此時交叉耦合系數(shù)約為0.1,，函數(shù)信號發(fā)生器的輸出阻抗R_S=R_L1=R_L2=50 Ω,。圖6為三線圈發(fā)生諧振時的雙負(fù)載電壓波形。

        從圖6中可以看出,，兩個接收線圈的電壓基本一致，說明發(fā)射線圈傳輸?shù)剿鼈兊墓β适窍嗤?，且試驗中發(fā)現(xiàn),，此時三線圈發(fā)生諧振，系統(tǒng)工作在最佳傳輸狀態(tài),，這也與式（7）的理論分析一致,。

        實驗中采用電容補(bǔ)償，由式(13)求得三線圈的補(bǔ)償電容分別為則由式(15)可得出補(bǔ)償后三線圈的可調(diào)諧電容分別為120 pF,、110 pF,、110 pF，此時三線圈同軸等間距5 cm放置時的雙負(fù)載電壓波形如圖7所示,。

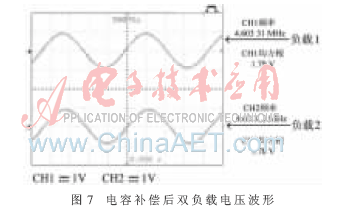
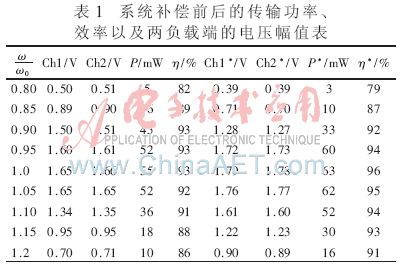
        從圖7中可以看出,，補(bǔ)償后兩負(fù)載電壓仍基本一樣，但是較未補(bǔ)償前電壓幅值有明顯提升,，且實驗中發(fā)現(xiàn),，此時效率是最高的。三線圈空間位置不變,，將系統(tǒng)的工作頻率分別調(diào)整為滿足ω/ω₀=0.8,、0.85、0.9,、0.95,、1.0,、1.05、1.1,、1.15,、1.2時，系統(tǒng)補(bǔ)償前后的傳輸功率,、效率以及兩負(fù)載端的電壓幅值如表1所示,。

        將以上實驗測量結(jié)果值在數(shù)值仿真解曲線圖中做出標(biāo)注，如圖8所示,。

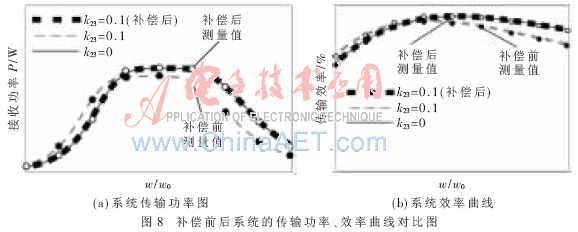
        從圖8的數(shù)值仿真曲線中可以發(fā)現(xiàn),，電容補(bǔ)償后系統(tǒng)的傳輸功率、效率曲線與k₂₃=0時系統(tǒng)的傳輸功率,、效率曲線完全重合,。將實驗測量結(jié)果值（表1）在數(shù)值解曲線中標(biāo)注后可以看出，實驗測量結(jié)果值在各測試點處與數(shù)值仿真解基本一致,，而且實驗中發(fā)現(xiàn),，在諧振頻率點4.6 MHz左右處系統(tǒng)所獲得的傳輸功率、效率也達(dá)到最大值,，兩負(fù)載端的傳輸功率最大為63 mW,，此時傳輸效率達(dá)到96 %左右。因此,，數(shù)值解和實驗測量值相比較的一致性充分說明本文所提出電抗補(bǔ)償方法的可行性和有效性,。

        對于兩個負(fù)載的諧振耦合式無線能量傳輸系統(tǒng)，兩負(fù)載間的交叉耦合效應(yīng)會對系統(tǒng)帶來一些不利的影響,，具體表現(xiàn)在兩負(fù)載線圈的電流幅值明顯減小,，電流相位發(fā)生偏離，系統(tǒng)的傳輸功率,、效率明顯降低,。通過在電路中附加電容補(bǔ)償?shù)姆椒苡行У氐窒徊骜詈闲?yīng)帶來的影響。從仿真和實驗的結(jié)果來看,，經(jīng)電容補(bǔ)償后,，無論是負(fù)載端電流幅值還是系統(tǒng)傳輸功率、效率都與無交叉耦合時幾乎相同,，很好地補(bǔ)償了交叉耦合對系統(tǒng)傳輸性能的影響,。本文分析和實驗中采用的是相同的收發(fā)線圈而且是同軸等間距放置的情況，不失一般性,，這種方法對于多個不同尺寸的線圈以及不同的線圈空間位置都具有指導(dǎo)意義和借鑒價值,。

參考文獻(xiàn)

[1] 趙爭鳴，張藝明，陳凱楠.磁耦合諧振式無線電能傳輸技術(shù)新進(jìn)展[J].中國電機(jī)工程學(xué)報,，2013,，33(3)：1-13.

[2] SOLJACJC M，KURS A,，KARALIS A,，et al.Wireless power transfer via strongly coupled magnetic resonances[J].Science，2007,，317(6)：83-85.

[3] KURS A,，MOFFATT R，SOLJACIC M.Simultaneous midrange power transfer to multiple devices[J].Applied Physics Letters,，2010,，96(4)：044102.

[4] 劉好．基于WiTricity技術(shù)的無線功率傳輸?shù)钠ヅ潆娐贩桨冈O(shè)計[D]．南昌：南昌大學(xué)，2012.