0 引言

    航空攝影（Aerial Photography）又稱航拍,，是指在飛機(jī)或其他航空飛行器上利用航空攝影機(jī)攝取地面景物相片的技術(shù),。目前，航空攝影應(yīng)用廣泛,，是獲取地理信息的主要手段^[1-2],。在航空攝影中，存在著一個(gè)難題需要解決：飛機(jī)在飛行攝影時(shí)會(huì)受到本機(jī)和氣流等的影響,，從而產(chǎn)生機(jī)體振動(dòng),，相機(jī)的姿態(tài)角也會(huì)隨著改變，相機(jī)姿態(tài)時(shí)刻改變就會(huì)給高精度拍攝帶來困難,。所以為提高航拍質(zhì)量,，必須對(duì)相機(jī)姿態(tài)進(jìn)行校正^[3]。

    校正的前提是獲取相機(jī)姿態(tài),，所以慣性測(cè)量元件必不可少,，但是單一的慣性測(cè)量元件無法給出準(zhǔn)確的姿態(tài)角，需要對(duì)多個(gè)慣性測(cè)量元件的數(shù)據(jù)進(jìn)行數(shù)據(jù)融合,。使用比較普遍的慣性測(cè)量元件的組合是加速度計(jì)和陀螺儀,。它們輸出的數(shù)據(jù)各有優(yōu)缺點(diǎn)，可以使用Kalman濾波對(duì)其進(jìn)行數(shù)據(jù)融合以得到準(zhǔn)確的姿態(tài)角^[4-5],。

    現(xiàn)有的實(shí)現(xiàn)Kalman濾波的方式主要有兩種：PC機(jī)和DSP,，兩者都存在著系統(tǒng)性能和成本不能兼顧的問題。而FPGA卻可以很好地解決這個(gè)問題,。本文主要講述的便是用FPGA實(shí)現(xiàn)Kalman濾波來獲取準(zhǔn)確的相機(jī)姿態(tài),。

1 坐標(biāo)模型

    在進(jìn)行航拍作業(yè)時(shí),，相機(jī)搭載在云臺(tái)上，云臺(tái)和飛機(jī)是一體的,，當(dāng)相機(jī)拍攝地面照片時(shí),，相機(jī)拍攝方向應(yīng)與地面垂直，如圖1所示,。

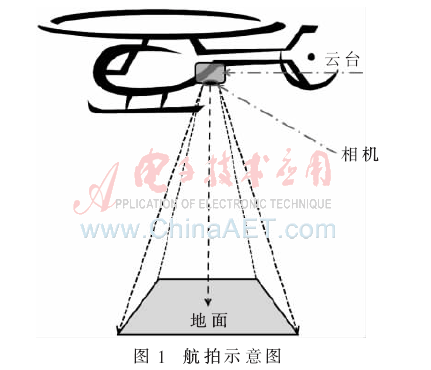
    為獲取相機(jī)姿態(tài),，首先以相機(jī)為原點(diǎn)，建立坐標(biāo)系,，如圖2所示,。其中，XY平面與地面平行,，Z軸垂直于地面,，Y軸方向?yàn)轱w機(jī)飛行方向。

    將加速度計(jì)固定在相機(jī)上,，當(dāng)相機(jī)姿態(tài)發(fā)生改變時(shí),，加速度的3個(gè)敏感軸便可以輸出在其相應(yīng)方向產(chǎn)生的重力分量信號(hào)，如圖2中的G_x,，G_y,，G_z所示。陀螺儀是一種角速度傳感器,，它可以輸出對(duì)應(yīng)軸上的瞬時(shí)角速度,，如圖2中的W_x，W_y,，W_z所示,。

    根據(jù)以上坐標(biāo)系，可以得到姿態(tài)角θ_x,，θ_y,，θ_z（分別代表著俯仰角、橫滾角,、偏航角）,，如式1所示，其中ΔT為采樣時(shí)間,，Δθ為采樣時(shí)間內(nèi)的姿態(tài)角變化,。

    可見，由加速度計(jì)或者陀螺儀都可以初步得到姿態(tài)角,，但是無論是加速度計(jì)還是陀螺儀,，它們輸出的原始數(shù)據(jù)都存在著固有缺陷：當(dāng)相機(jī)處于變速運(yùn)動(dòng)狀態(tài)時(shí)，加速度計(jì)的輸出并不是重力加速度,，而是重力加速度和其自身加速度的矢量和,。陀螺儀是通過對(duì)角速度積分得到姿態(tài)角，隨著時(shí)間的推移,，姿態(tài)角的誤差會(huì)越來越大。所以單一的加速度計(jì)或者陀螺儀都無法獲得正確的姿態(tài)角,，必須對(duì)兩者進(jìn)行數(shù)據(jù)融合,。

2 Kalman濾波模型的建立

    Kalman濾波是在時(shí)域內(nèi)以信號(hào)的一、二階統(tǒng)計(jì)特性已知為前提,、以均方誤差極小為判據(jù),，能自動(dòng)跟蹤信號(hào)統(tǒng)計(jì)性質(zhì)的非平穩(wěn)變化，具有遞歸性質(zhì)的一種算法^[5],。Kalman濾波的狀態(tài)方程和預(yù)測(cè)方程如式(2)所示：

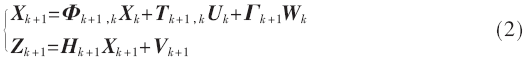
其中,，X_k+1為系統(tǒng)的狀態(tài)向量，Φ_k+1,，k為狀態(tài)轉(zhuǎn)移矩陣,，T_k+1，k為控制系數(shù)矩陣,，U_k為系統(tǒng)控制輸入,，Γ_k+1為噪聲系數(shù)矩陣，W_k為系統(tǒng)的過程噪聲序列,，Z_k+1為系統(tǒng)的觀測(cè)序列,，H_k+1為觀測(cè)矩陣，V_k+1為觀測(cè)噪聲序列,。

    使用陀螺儀數(shù)據(jù)建立線性模型,，如式(3)所示：

其中，θ_k為飛行姿態(tài)角,，β_k為陀螺儀輸出的誤差,，U_k是陀螺儀輸出的角速度數(shù)據(jù)，ΔT是采樣時(shí)間間隔,。因?yàn)橥勇輧x輸出的誤差整體來看變化不大,，可認(rèn)為β_k+1=β_k。因W_k對(duì)系統(tǒng)影響甚小,，這里規(guī)定W_k=0,。

    由以上建立狀態(tài)矩陣方程，如式(4)所示：

    陀螺儀和加速度計(jì)測(cè)量姿態(tài)角時(shí)各有優(yōu)缺點(diǎn),，為獲得比較可靠的姿態(tài)角數(shù)據(jù),，必須對(duì)兩者的數(shù)據(jù)優(yōu)勢(shì)互補(bǔ)。以上算法用加速度計(jì)數(shù)據(jù)得到不同階段的測(cè)量噪聲協(xié)方差,，并帶入解算過程中,，大大減少了姿態(tài)角的測(cè)量誤差。

3 Kalman硬件實(shí)現(xiàn)

    目前Kalman濾波器的實(shí)現(xiàn)方式主要有PC機(jī)和DSP兩種方式,，PC機(jī)可以同時(shí)滿足計(jì)算精度和實(shí)時(shí)性的要求,，但是PC機(jī)體積大、質(zhì)量重,、成本高,；DSP實(shí)現(xiàn)的Kalman濾波器雖然體積小，質(zhì)量輕,，但是因其指令順序執(zhí)行的CPU架構(gòu),，在系統(tǒng)復(fù)雜時(shí)無法滿足系統(tǒng)的實(shí)時(shí)性要求^[6-7],。

    因此,，Kalman濾波器在工程應(yīng)用中的實(shí)現(xiàn)遇到了系統(tǒng)體積,、重量,、成本與系統(tǒng)精度、速度等性能不能兼顧的問題,。FPGA是解決這一問題的有效途徑，F(xiàn)PGA具有極高并行度的信號(hào)處理能力,、高度的靈活性,、現(xiàn)場(chǎng)可以編程、較短的開發(fā)周期和較低的成本等優(yōu)勢(shì),，在數(shù)字信號(hào)處理領(lǐng)域已經(jīng)得到廣泛的應(yīng)用^[8]。

    本系統(tǒng)使用的FPGA芯片是Altera公司Cyclone II系列中的EP2C35F672C6,，它共有33 216個(gè)邏輯單元,、483 840個(gè)存儲(chǔ)單元,、70個(gè)乘法器單元（9 bit）,。雖然Altera公司提供了很多功能強(qiáng)大的IP核，其中就包括加減乘除單精度浮點(diǎn)數(shù)運(yùn)算,，但是提供的IP核占用資源過多,，所以使用自己編寫的運(yùn)算模塊。下面以除法模塊為例說明浮點(diǎn)數(shù)運(yùn)算的硬件實(shí)現(xiàn),。

3.1 浮點(diǎn)數(shù)除法模塊

    根據(jù)IEEE754標(biāo)準(zhǔn),，單精度浮點(diǎn)數(shù)的格式如圖2所示。

    通常可用式(11)表示一個(gè)單精度浮點(diǎn)數(shù)：

    從式(12)中可以看到,，符號(hào)位和階碼的運(yùn)算比較簡(jiǎn)單,，尾數(shù)的運(yùn)算較為復(fù)雜。

    設(shè)被除數(shù)為a,，除數(shù)為b,，第i次的商為qi，第i次得到的臨時(shí)余數(shù)為mi,，令m0=a,，則有式(13)：

    這樣一直進(jìn)行23次運(yùn)算便可以獲得全部的q_i,，23位q_i按先后順序組合起來便是尾數(shù)運(yùn)算的結(jié)果。

    除法模塊資源使用情況如圖3所示,，只使用了1%的邏輯單元,，相比較于IP核的實(shí)現(xiàn)方式，大大減少了使用資源,。

    再用ModelSim仿真觀察除法模塊運(yùn)算速度,，結(jié)果如圖4所示。x1,，x2是除數(shù)和被除數(shù),，y是商，isdone是標(biāo)志信號(hào),，當(dāng)完成一次除法運(yùn)算后產(chǎn)生一個(gè)正脈沖,。

    由圖4可以看到，除法模塊運(yùn)算一次共使用了25個(gè)CLK周期,，完全可以滿足運(yùn)算要求,。

3.2 Kalman硬件模塊

    以第2節(jié)中建立的卡爾曼濾波模型搭建硬件模塊，硬件模塊的結(jié)構(gòu)如圖5所示,。其中,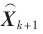，為整個(gè)Kalman濾波的結(jié)果矩陣，包括橫滾角,、俯仰角,、偏航角。

    Kalman硬件模塊使用資源情況如圖6所示,?？梢姡还彩褂昧?5%的邏輯單元,。雖然占用資源非常多,，但是45%的資源使用還是可以接受的。

    利用Multisim仿真，查看此Kalman硬件模塊的運(yùn)行速度,，結(jié)果如圖7所示,。

q1、q2,、q3是Kalman濾波解算一次后的3個(gè)偏轉(zhuǎn)角（橫滾角,、俯仰角、航向角）,，q1st,、q2st、q3st是解算一次完成后產(chǎn)生的負(fù)脈沖信號(hào),。從仿真結(jié)果來看,，在仿真頻率為100 MHz情況下，Kalman解算一次需要的時(shí)間是1 ms,，可見用FPGA來實(shí)現(xiàn)Kalman濾波速度是很快的,。

4 實(shí)驗(yàn)結(jié)果

    為檢驗(yàn)Kalman濾波硬件模塊實(shí)際效果，設(shè)計(jì)了一次模擬實(shí)驗(yàn)：將云臺(tái)置于振動(dòng)環(huán)境中,，改變?cè)婆_(tái)姿態(tài)角,，觀察未經(jīng)濾波處理和經(jīng)過濾波處理的姿態(tài)角。

    實(shí)驗(yàn)中使用MPU6050作為系統(tǒng)的姿態(tài)傳感器,，MPU-6050是一款整合了3軸陀螺儀,、3軸加速度計(jì)的6軸運(yùn)動(dòng)處理組件，相比較于多組件方案,，免除了組合陀螺儀與加速度計(jì)時(shí)之軸間差的問題,，減少了大量的包裝空間。

    設(shè)置采樣頻率為1 kHz,，以橫滾角為示例,，實(shí)驗(yàn)結(jié)果如圖8所示。

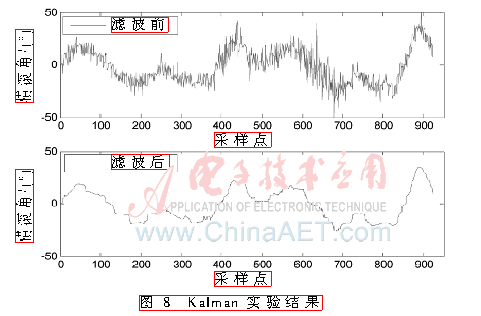
    濾波前的橫滾角由三軸加速度和式（1）得到,，可以看到明顯的噪聲和毛刺,。經(jīng)過Kalman濾波后，大部分的噪聲和毛刺都被去除掉了,，而且通過濾波前后的橫坐標(biāo)對(duì)比可以看到此濾波模塊有著很好的實(shí)時(shí)性能,。

    觀察濾波結(jié)果與真實(shí)值之間的誤差，如圖9所示,。從圖中可以看到,，濾波誤差控制在-1.5°～1.5°范圍內(nèi)?？梢詽M足航拍系統(tǒng)的精度要求,。

5 結(jié)論

    實(shí)驗(yàn)證明,，本文所介紹的硬件Kalman濾波器適用于航拍相機(jī)平臺(tái)的姿態(tài)獲取?；贔PGA的硬件架構(gòu)具有靈活的可移植特性和優(yōu)良的抗干擾能力,，相比較于DSP和PC機(jī)的實(shí)現(xiàn)方式，它在保證航拍系統(tǒng)的精度要求的前提下解決了性能和成本不能兼顧的問題,，因此它具有更廣泛的應(yīng)用性和實(shí)際工程意義,。

參考文獻(xiàn)

[1] 劉先林，段福洲,，宮輝力.航空攝影科技發(fā)展成就與未來展望[J].前沿科學(xué),，2007，3(3)：10-14.

[2] 張祖勛.數(shù)字?jǐn)z影測(cè)量發(fā)展與展望[J].地理信息世界,，2004,，2(3)：1-5.

[3] 高同躍，丁衛(wèi),，高新聞，等.機(jī)載慣性穩(wěn)定云臺(tái)系統(tǒng)的研究[J].2010,，18(2)：344-347.

[4] 卞鴻巍,李安,覃方君,，等.現(xiàn)代信息融合技術(shù)在組合導(dǎo)航中的應(yīng)用[M].北京：國防工業(yè)出版社，2010.

[5] 付夢(mèng)印,，鄧志紅,，閆莉萍.Kalman濾波理論及其在導(dǎo)航系統(tǒng)中的應(yīng)用(第二版)[M].北京：科學(xué)出版社，2010.

[6] 謝鑫,，郭美鳳,，周斌.基于雙DSP和FPGA的高性能導(dǎo)航計(jì)算機(jī)設(shè)計(jì)[J].微計(jì)算機(jī)信息，2009(3)：1-2,，60.

[7] 張沖,，吳秋平.基于PC104和DSP的分布式導(dǎo)航計(jì)算機(jī)設(shè)計(jì)[J].微計(jì)算機(jī)信息，2010(8)：27-29.

[8] 米月琴,，黃軍榮.基于FPGA的Kalman濾波器的設(shè)計(jì)[J].電子科技,，2010，23(2)：52-55.