摘 要: 提出了一種過濾冗余特征的算法框架,利用組特征選擇算法去除冗余特征,。在組構造階段為了彌補單一聚類算法的不足,,引入聚類集成的思想,先利用k-means方法通過多次聚類得到一個聚類集體,,在集成階段再利用層次聚類算法對聚類集體進行集成得到最終的結果,。實驗結果表明,這種算法框架能有效消除冗余特征,,在保證算法穩(wěn)定性的同時還能獲得很好的性能,。
關鍵詞: 穩(wěn)定性;組特征選擇,;聚類集成,;層次聚類
特征選擇[1]指從一組特征中挑選出一些最有效的特征以達到降低特征空間維數(shù)的目的的過程,是模式識別和機器學習領域中一項必不可少的技術,,在數(shù)據(jù)預處理中發(fā)揮重要作用,,它廣泛應用于文本分類,、生物信息學和信息檢索等方面,。尤其在海量高維數(shù)據(jù)不斷涌現(xiàn)的今天,許多機器學習算法受不相關和冗余特征的影響,,而通過選擇合適的特征選擇算法,,可以有效地去除不相關、冗余特征,,加速數(shù)據(jù)挖掘的過程,,提高學習算法的泛化性能和運行效率,得到更加簡單和容易理解的學習模型[2-3],。
圍繞提高分類性能和降低特征維數(shù)已經(jīng)提出了很多算法,,但是人們往往忽視特征選擇的穩(wěn)定性即特征選擇算法的結果對于訓練集變化的敏感程度,用于度量訓練集的細微變化對最優(yōu)特征子集的影響[4],。這個問題在很多應用中是很重要的,,例如在分析微陣列數(shù)據(jù)時,由于訓練數(shù)據(jù)的微小變化,,同一個特征選擇算法可能會選擇出差異很大的特征子集,,雖然大多數(shù)的特征子集在分類性能方面同樣優(yōu)秀[5-6]。這種不穩(wěn)定性挫傷了領域專家對于生物標志物識別的信心,。
目前,,穩(wěn)定性問題已成為特征選擇的一個研究熱點,吸引了眾多學者的研究,。提高特征選擇穩(wěn)定性的方法主要有3種:(1)借鑒集成學習的思想,,利用集成特征選擇有效地提高特征選擇的穩(wěn)定性;(2)樣本注入的方式;(3)組特征選擇[7],。
本文將集成方法和組特征選擇方法進行結合,,提出了一種基于特征聚類集成技術的組特征選擇方法,用于提高算法的穩(wěn)定性,。在組構造階段利用聚類集成的思想對特征進行聚類,,彌補單一聚類方法的不足。在組變換階段,,從每個特征組中選出一個特征來代表這個組,,最終就得到了最優(yōu)的特征子集。
1 組特征選擇
相關的特征組通常存在于高維數(shù)據(jù)中,,并且這樣的特征組對于訓練樣本的改變存在抵抗作用[8],。如果把每個特征組看作是一個相關的單獨實體,這樣既可以去除冗余特征,,也可以起到提高特征選擇穩(wěn)定性的效果?,F(xiàn)有的組特征選擇算法的通用算法框架如圖1所示。組特征選擇包括組構造和組變換兩個關鍵步驟,。

1.1 特征組構造
組構造是識別相關特征組的過程,,特征組的識別包括知識驅動方法和數(shù)據(jù)驅動方法兩類不同的方法。知識驅動方法利用領域知識使得特征組的產(chǎn)生變得容易,;而數(shù)據(jù)驅動方法僅考慮原始的數(shù)據(jù),,并不考慮領域相關的信息。
數(shù)據(jù)驅動方法利用聚類分析[9]或者密度估計[6]來識別特征簇(組),。在聚類分析方法中通常采用經(jīng)典的劃分算法,,例如層次聚類或者k均值等方法來產(chǎn)生特征組。需要注意的是,,大多數(shù)現(xiàn)有的聚類方法沒有明顯地考慮特征組的穩(wěn)定性,。
數(shù)據(jù)驅動方法充分地利用了目標數(shù)據(jù)的特性,因此現(xiàn)在被廣泛應用,。它的一個最主要的缺點就是不容易解釋和驗證所選擇的特征組,。
1.2 特征組變換
特征組變換即從每個特征組中產(chǎn)生一個單獨的相關特征來代表這個特征組。通過從每個組中選擇一個代表特征,,這樣就解決了特征冗余的問題,。變換方法從簡單的特征值平均[10]到復雜的組成分分析方法[11]等。本文采用的是求中心點的策略,。
2 特征聚類集成方法
假設給定一個訓練樣本D,,它包括n個樣本,D={X,,Y}={xi,,yi},,該數(shù)據(jù)集中的第i個元素xi為一個d維向量xi=(xi1,xi2,,…,,xid)∈Rd。
聚類集成算法要解決的主要問題有兩個,,一是如何產(chǎn)生不同的聚類從而形式一個聚類集體,,二是如何從這個聚類中得到一個統(tǒng)一的聚類結果,也可稱為集成問題,。
2.1 聚類集體生成
在知識驅動方法中采用的聚類分析方法,,是無監(jiān)督特征選擇的一個重要方法。但由于聚類分析的不可能性定理[12],,即任何一個聚類算法不可能同時滿足尺度不變性,、豐富性和一致性,這樣就導致沒有一個聚類算法可以很好地適用于任何問題,。為了解決這個問題,,借鑒集成學習[13]的思想,通過組合不同的弱基類模型得到一個性能好的集成模型,。因此本文提出一個新的組構造策略,,即聚類集成的方法,它可以在不同領域和數(shù)據(jù)集上有更好的平均性能,,能發(fā)現(xiàn)任何單個聚類算法無法得到的結合解答[14],。
在組構造階段,,使用相同的算法在數(shù)據(jù)集的不同采樣集合上聚類,,從而得到多個聚類結果[15]?;赽agging[16]方法,,通過可放回抽樣獲取不同的訓練樣本子集來訓練基聚類器。假設通過bagging方法得到m個不同的訓練子集{D1,,D2,,…,Dm},,單個聚類器采用k-means方法,,其中特征之間的相似性度量策略選用相關系數(shù)。
在m個訓練子集上進行多次k-means聚類,,得到m個聚類結果,,每個聚類結果包括多個特征組,即{F,,F(xiàn),,…,,F(xiàn),…,,F(xiàn)},,F(xiàn)代表在i次k-means聚類得到的第j個特征組,F(xiàn)代表第m次聚類得到Lm個特征組,。
2.2 特征聚類集成策略
在組構造階段得到聚類集體后,,就需要設計合適的集成方法對多個聚類結果進行集成,這也是聚類集成中的關鍵問題,。本文采用基于互聯(lián)合矩陣[17]的方法,,即在得到的聚類集體{F,F(xiàn),,…,,F(xiàn),…,,F(xiàn)}中,,計算在所有的特征組F中每對特征被分到一個組的次數(shù),除以集成的次數(shù)m,,得到每個特征對的相似性Wi,,j,再利用凝聚的層次聚類將所有的特征進行聚類得到集成的特征組{EF1,,EF2,,…,EFL},。為了降低異常值的影響,,采用類平均法利用兩組特征的相似性來決定是否將它們合并。合并的過程一直持續(xù)只要兩個特征組的相似性>閾值?茲,。?茲是一個用戶參數(shù),,可以根據(jù)不同的數(shù)據(jù)集進行調整。
層次聚類算法需要計算簇與簇之間的距離,,目前常用的計算簇間距離的方法有:最短距離法,、最長距離法和類平均法。其中類平均法很好地利用所有樣本之間的信息,,它傾向于合并差異小的兩個類,,考慮到類的結構,產(chǎn)生的分類具有相對的魯棒性,。
本文中提出的算法使用類平均法,,兩個簇間的距離等于所有分別來自兩個簇的點對間的距離的平均值,給定要聚類的對象即d個特征以及d×d的相似行矩陣W,,具體的層次聚類方法的步驟如下:
?。?)將每個特征歸為一簇,,共得到d簇,每簇僅包含一個特征,。簇與簇之間的距離就是兩個特征間的相似性,。
(2)根據(jù)相似性矩陣W,,若兩簇的相似性Wi,,j大于閾值?茲,則將這兩簇合并成一簇,,于是總的簇數(shù)少了一個,。
(3)重新計算新的簇與所有舊簇之間的相似性,,計算方法采用類平均法,。
(4)重復(2),、(3)步,,直到類之間的相似性全都小于閾值?茲,則聚類結束,。
經(jīng)過以上步驟得到組構造階段產(chǎn)生的集成特征組{EF1,,EF2,…,,EFL},,在組變換階段,需要從每個特征組中產(chǎn)生一個單獨的相關特征來代表這個特征組,。先對組構造階段產(chǎn)生的特征組中的所有特征求平均,,得到每個組的中心點,再計算組中的所有點到中心點的距離,,最后將距離中心點最近的那個點作為特征組的代表特征,。這樣在組特征選擇階段就得到去除了冗余特征的特征子集{f1,f2,,…,fL},。算法的偽代碼如下:
基于特征聚類集成技術的組特征選擇方法
輸入:數(shù)據(jù)集D,,m個子樣本
輸出:選擇出的特征{f1,f2,,…,,fL}
//組構造階段
for i=1,2,,…,,m
從D中可放回抽樣得到訓練樣本Di
調用k-means方法得到特征組
end for
for對每一個特征對xi,,xj∈D
令Wij=xi和xj分到一組的次數(shù)/m
end for
基于Wij將所有的特征進行層次聚類,得到集成特征組{EF1,,EF2,,…,EFL}
//組變換階段
for i=1,,2,,…,L
從EFi中獲取代表特征xi
end for
3 實驗
為了驗證所提算法的性能,,將在不同的基準數(shù)據(jù)集上進行實驗以此來驗證算法的穩(wěn)定性和分類性能,。實驗所用數(shù)據(jù)集為:Sonar,Toy,,Hill-Valley,,Spect Heart,Madelon,,Genes均來自UCI數(shù)據(jù)庫[18],,Colon cancer diagnosis數(shù)據(jù)集來自參考文獻[19]。各個數(shù)據(jù)集的詳細信息如表1所示,。
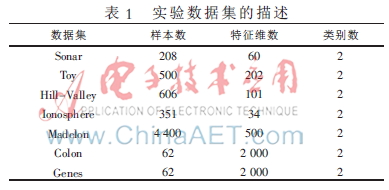
實驗選取兩種集成特征選擇方法和一種樣本加權方法,,用來和本文提出的EFC算法進行對比。它們分別是集成Relief算法(En-relief),、集成fisher score[20]算法(En-fisher score)和樣本加權算法VR-Lmba,。
3.1 穩(wěn)定性實驗
為了驗證本文所提算法的穩(wěn)定性,采取基于bagging方法的可放回抽樣,。首先,,對于非集成方法VR-Lmba,對原始數(shù)據(jù)集進行10次可放回抽樣,,每次隨機抽取90%(觀察樣本的微小變化)的樣本構成新的訓練樣本子集,,計算VR-Lmba算法的平均穩(wěn)定性;其次,,計算En-relief,、En-fisher score兩個集成算法的穩(wěn)定性,利用集成思想在訓練子集上進行二次抽樣,,采樣比例為90%,,在得到的樣本子集上進行集成特征選擇,得到m個不同的特征權重向量,。再利用線性加權集成方法,,獲取每個訓練子集的集成結果,最后計算特征子集間的平均穩(wěn)定性,;對于EFC算法,,與上述集成方法的實驗方法相同,,不同的是EFC算法的輸出是10個特征子集,無需線性集成的過程,。其中,,計算一對特征子集穩(wěn)定性的方法是杰卡德系數(shù)[21],最終的穩(wěn)定性是所有不同特征子集對的平均穩(wěn)定性,。算法的穩(wěn)定性對比實驗結果如圖2所示,。X軸代表基特征選擇器的個數(shù)m。VR-Lmba算法不是集成算法,,因此它的穩(wěn)定性不會隨m值變化,。
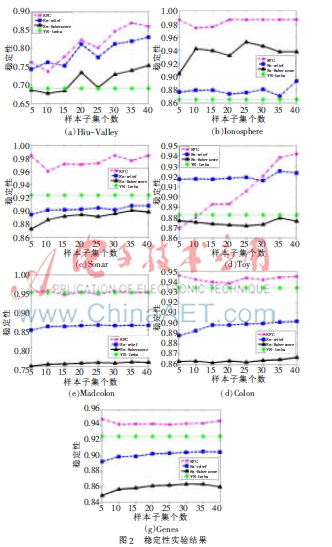
通過以上穩(wěn)定性的對比實驗,可以觀察到EFC算法的穩(wěn)定性與其他算法相比有相似或者高于它們的穩(wěn)定性,。而且隨著基特征選擇器數(shù)目的增加,,穩(wěn)定性也隨之提高,當基特征選擇器到達一定數(shù)目后,,穩(wěn)定性基本保持不變,。
3.2 分類準確率實驗
由于不存在普遍接受的聚類性能的評價指標,本文將利用分類準確率來驗證所提算法的性能,。實驗采用10次交叉驗證,,分類器選取k(k=3)近鄰分類器和線性SVM(C=1)分類器,集成特征選擇基分類器的個數(shù)m=20,。4種算法的分類準確率實驗結果如表2和表3所示,,分別對應3NN和SVM分類器。
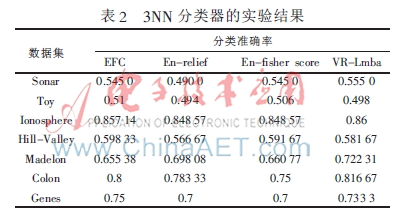
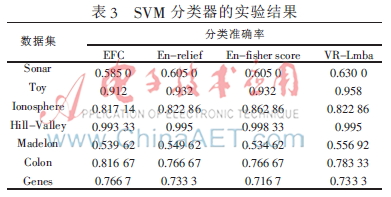
本文提出了一種過濾冗余特征的算法框架,,利用組特征選擇算法去除冗余特征,,在組構造階段引入聚類集成的思想,集成方法采用基于互聯(lián)合矩陣的方法,,利用基于相似性的層次聚類算法對聚類集體進行集成,。
實驗結果表明所提算法能有效消除冗余特征,保證算法穩(wěn)定性的同時還能獲得很好的性能,,能有效地處理高維和噪聲數(shù)據(jù),。算法的不足之處就是集成階段,由于層次聚類中使用距離矩陣,,所以它的時間和空間復雜性都是二次以上的,,這也是未來對本論文所提算法的一個改進方向。
參考文獻
[1] 張學工.模式識別(第三版)[M].北京:清華大學出版社,,2010.
[2] DASH M, LIU H. Feature selection for classification[J]. Intelligent data analysis,, 1997,, 1(1-4):131-156.
[3] KOHAVI R,, JOHN G H. Wrappers for feature subset selection[J]. Artificial intelligence,1997,,97(1):273-324.
[4] K P,, K J, H V. Improving stability of feature selection methods[C]. Proceedings of the 12th International Conference on Computer Analysis of Images and Patterns,, 2007:929-936.
[5] KALOUSIS A,, PRADOS J, HILARIO M. Stability of feature selection algorithms: a study on high-dimensional spaces[J]. Knowledge and Information Systems,, 2007(12):95-116.
[6] YU L,, DING C, LOSCALZO S. Stable feature selection via dense feature groups[J]. Proceedings of the 14th ACM International Conference on Knowledge Discovery and Data Mining,, 2008:803-811.
[7] AWADA W,, KHOSHGOFTAAR T M, DITTMAN D,, et al. A review of the stability of feature selection techniques for bioinformatics data[C]. 2012 IEEE 13th International Conference on,, Information Reuse and Integration, IEEE,, 2012: 356-363.
[8] LOSCALZO S,, YU L, DING C. Consensus group stable feature selection[C]. Proceedings of the 15th ACM SIGKDD international conference on Knowledge discovery and data mining,, 2009: 567-576.
[9] AU W H,, CHAN K C C, WONG A K C,, et al. Attribute clustering for grouping,, selection, and classification of gene expression data[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics (TCBB),, 2005,, 2(2): 83-101.
[10] GUO Z, ZHANG T,, LI X,, et al. Towards precise classification of cancers based on robust gene functional expression profiles[J]. BMC Bioinformatics,2005,,6(1):58.
[11] RAPAPORT F,, ZINOVYEV A, DUTREIX M,, et al. Classification of microarray data using gene networks[J]. BMC Bioinformatics,, 2007,8(1):35.
[12] KLEINBERGJ. An impossibility theorem for clustering[C]. Advances in Neural Information Processing Systems, 2002:446-453.
[13] DIETTERICH T G. Ensemble methods in machine learning[C]. Proceedings of the 1st International Workshop on Multiple Classifier Systems,, Cagliari,, Italy, 2000:1-15.
[14] 羅會蘭.聚類集成關鍵技術研究[D].浙江:浙江大學,,2007.
[15] STREHL A,, GHOSH J. Cluster ensembles-a knowledge reuse framework for combining multiple partitions[J]. Journal of Machine Learning Research, 2002(3):583-617.
[16] GAO J,, FAN W,, HAN J. On the power of ensemble: Supervised and unsupervised methods reconciled[C]. Tutorial on SIAM Data Mining Conference (SDM),2010.
[17] FRED ALN. Finding consistent clusters in data partitions[C]. Multiple Classifier Systems,,2001:309-318.
[18] FRANK A,, ASUNCION A. UCI machine learning repository[DB]. http://archive.ics.uci.edu/ml.2010.
[19] ALON U, BARKAI N,, NOTTERMAN D A,, et al. Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon cancer tissues probed by oligonucleotide arrays[J]. Proceedings of the National Academy of Sciences of the United States of America, 1999: 6745-6750.
[20] TSUDA K,, KAWANABE M,, MO?譈LLER K R. Clustering with the fisher score[J]. Advances in Neural Information Processing Systems, 2002(15):729-736.
[21] HE Z Y,, YU W C. Stable feature selection for biomarker discovery[J]. Computational Biology and Chemistry,, 2010,
34(4):215-225.

