摘  要： 在高空高速條件下，GPS信號失鎖致使常規(guī)的卡爾曼濾波器發(fā)散，從而導致組合導航系統(tǒng)精度嚴重下降,。以BP神經(jīng)網(wǎng)絡輔助技術手段對GPS/INS組合導航濾波算法實施精度補償,，即在GPS信號鎖定時，對神經(jīng)網(wǎng)絡進行實時在線訓練,，而當在GPS信號失鎖時,，利用之前訓練好的神經(jīng)網(wǎng)絡進行組合導航濾波，以解決精度嚴重下降問題,。算法采用多神經(jīng)網(wǎng)絡并行結構,，以減少神經(jīng)網(wǎng)絡在訓練過程中的交叉耦合，提高訓練速度,。通過MATLAB仿真,，驗證了算法的可靠性與可行性，并證明其在GPS信號丟失時,，精度較純慣性導航系統(tǒng)有較大提高,。

    關鍵詞： 卡爾曼濾波；組合導航,；GPS/INS,； BP神經(jīng)網(wǎng)絡

0 引言

    GPS/INS組合導航系統(tǒng)由于其高精度、高可靠性,、具有全天候工作能力等突出優(yōu)點,，成為組合導航系統(tǒng)的主要發(fā)展方向之一，被廣泛應用于軍事和民用等領域的導航,。

    卡爾曼濾波技術和BP神經(jīng)網(wǎng)絡技術都是現(xiàn)今發(fā)展較為成熟的技術,，但其單獨作為組合導航系統(tǒng)濾波算法時，都存在一些不足,?？柭鼮V波技術是現(xiàn)今發(fā)展較好的組合導航系統(tǒng)濾波技術，大量應用于生產(chǎn)生活中,，其設計簡單,、適用性好、精度高的特點受到人們的青睞,。然而,，在高空高速條件下，GPS信號容易失鎖,，從而造成卡爾曼濾波器發(fā)散等問題,。BP神經(jīng)網(wǎng)絡本身具有非線性、自組織和自學習能力,，適合于解決非線性問題,，但是,，將其單獨應用于組合導航濾波時，精度相對較低,，不能滿足導航精度要求,。

    本文將BP神經(jīng)網(wǎng)絡輔助卡爾曼濾波算法應用于GPS/INS組合導航系統(tǒng)，其精度要明顯優(yōu)于兩者單獨采用時的濾波器,。兩者的組合方式分為松散組合和緊密組合兩種,，其各有優(yōu)缺點。緊密組合的導航精度雖然較松散組合更高,，但當GPS衛(wèi)星失鎖完全無信號輸出時,，該組合方式失效，不能起到濾波作用,。另外,，采用緊密組合方式結構復雜，計算量大,，故本文采用了松散組合方式,。此方式具有結構簡單、可靠性高,、容錯能力強等優(yōu)點,，是動態(tài)測量質(zhì)量的可靠保證。

1 系統(tǒng)結構

    基于BP神經(jīng)網(wǎng)絡輔助卡爾曼濾波的GPS/INS組合導航系統(tǒng)結構如圖1所示,。組合導航系統(tǒng)濾波分為2種模式：卡爾曼濾波模式和BP神經(jīng)網(wǎng)絡預測模式,。當GPS信號鎖定時，組合導航系統(tǒng)采用卡爾曼濾波模式,，卡爾曼濾波器的輸入為INS和GPS的速度,、位置差值，經(jīng)過卡爾曼濾波之后,，輸出量為：

式中：[ΔV_E  ΔV_N  ΔV_U]為東向,、北向、天向速度誤差,，[Δλ  ΔL  Δh]為經(jīng)度,、緯度、高度誤差,。

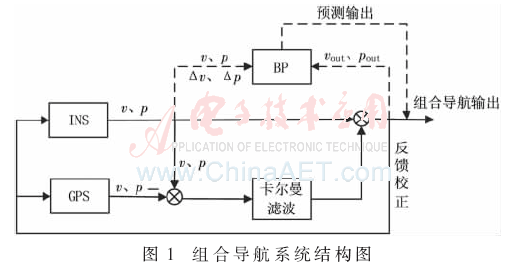
    卡爾曼濾波的輸出量與INS的輸出量相組合,，得到組合導航系統(tǒng)的最終輸出，并用該最終輸出對INS和GPS子導航系統(tǒng)進行反饋校正,。與此同時，對BP神經(jīng)網(wǎng)絡進行在線訓練,。

    BP神經(jīng)網(wǎng)絡在線訓練時,，為了避免訓練過程中的交叉耦合,，提高訓練精度和速度，減少神經(jīng)網(wǎng)絡權值不必要的調(diào)整,，本文采用了多BP神經(jīng)網(wǎng)絡并行結構,，訓練BP神經(jīng)網(wǎng)絡時的輸入分別為INS的3個速度分量和3個位置分量，以及其與前一時刻的速度分量,、位置分量的差值,，組合導航系統(tǒng)的最終輸出作為訓練神經(jīng)網(wǎng)絡的目標，對BP神經(jīng)網(wǎng)絡進行在線訓練,。

    當GPS信號失鎖不可用時,，卡爾曼濾波模式發(fā)散，精度嚴重下降,，故采用BP神經(jīng)網(wǎng)絡預測模式,。

2 卡爾曼濾波設計

    卡爾曼濾波的狀態(tài)方程和量測方程分別為：

    式中，Φ_K,，K-1為一步轉移陣,，Γ_K-1為系統(tǒng)噪聲驅動陣，H_K為量測陣,；V_K為量測噪聲序列,；W_K為系統(tǒng)激勵噪聲序列。

    在組合導航系統(tǒng)濾波算法設計時,，將GPS的位置,、速度信號和INS的位置、速度信號的差值作為卡爾曼濾波器的觀測量,，X_K按下面方程求解[1]：

3 BP神經(jīng)網(wǎng)絡設計

    BP神經(jīng)網(wǎng)絡具有非線性,、自組織和自學習能力，適合于解決非線性問題,，是現(xiàn)今發(fā)展較為成熟的技術,。理論研究表明，單隱層的BP神經(jīng)網(wǎng)絡可以進行任意的曲線逼近,，結構簡單,，效果明顯。

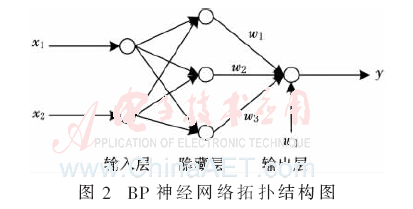
3.1 BP神經(jīng)網(wǎng)絡模型設計

    BP神經(jīng)網(wǎng)絡拓撲結構分為輸入層,、隱含層,、輸出層，如圖2所示,。其中,，隱含層為非線性層，采用sigmoid函數(shù)：

    而輸出層為線性層,，采用的函數(shù)為線性函數(shù),。

    BP神經(jīng)網(wǎng)絡的前向計算公式為^[2]：

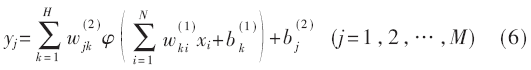
式中,，w為神經(jīng)元之間的權值，M為輸出層節(jié)點數(shù),，H為隱層節(jié)點數(shù),，N為輸入層節(jié)點數(shù)，b為神經(jīng)元內(nèi)的閾值,。

    本文采用的神經(jīng)網(wǎng)絡輸入層有2個神經(jīng)元,，輸出層為1個神經(jīng)元。隱含層神經(jīng)元數(shù)目由式(7)確定：

式中,，k為訓練樣本個數(shù),。

3.2 神經(jīng)網(wǎng)絡的工作模式

    本文設計的神經(jīng)網(wǎng)絡主要有在線訓練模式和預測輸出模式。當GPS信號鎖定時,，利用組合導航系統(tǒng)最終輸出對神經(jīng)網(wǎng)絡的在線實時訓練,，當GPS信號失鎖時，組合導航系統(tǒng)只剩下INS輸出,，這時,，采用神經(jīng)網(wǎng)絡預測模式，對INS輸出進行調(diào)整,，達到減少組合導航系統(tǒng)誤差,、提高導航精度的目的。

4 仿真驗證

    本文采用MATLAB軟件對神經(jīng)網(wǎng)絡輔助的組合導航濾波算法進行仿真驗證,，仿真時間為900 s,。仿真中，陀螺漂移,、GPS速度和位置都看作是馬爾科夫過程,，參數(shù)設置如下^[3]：

    陀螺漂移均方值0.1°/h，相關時間100 s,；GPS速度誤差均方值0.1 m/s,，相關時間5 s；GPS位置誤差均方值20 m,、相關時間10 s,。

    由以上參數(shù)設置得到純慣導的速度誤差、位置誤差的仿真圖像如圖3,、圖4所示,。

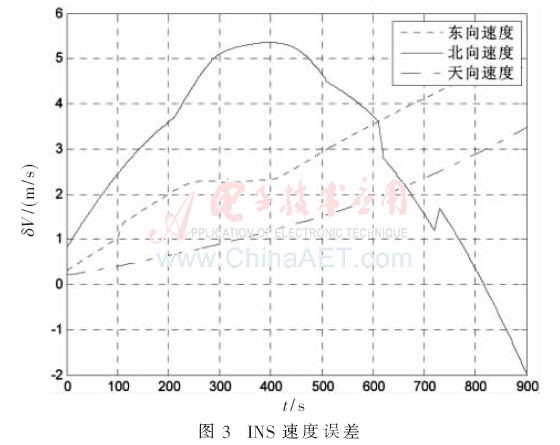
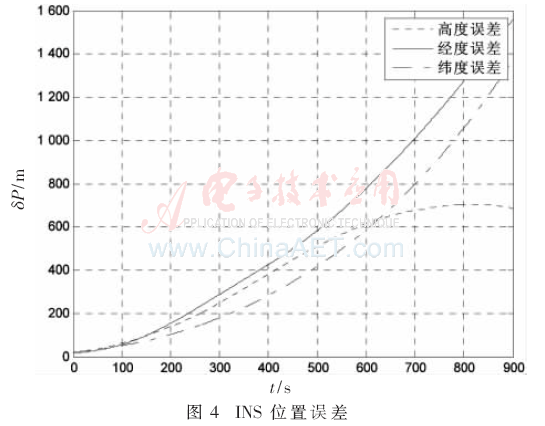
    通過理論與仿真圖像可知，純慣導的速度誤差和位置誤差隨著時間發(fā)散,，在仿真的900s中,，東向速度最大誤差為5 m，北向速度最大誤差為6 m，天向速度最大誤差為4 m,。所得數(shù)據(jù)與實際相符合,，仿真有效,。

    在仿真中,，設置t=700 s之前組合導航系統(tǒng)鎖定GPS，所用的濾波算法為卡爾曼濾波,，同時,，在線實時訓練神經(jīng)網(wǎng)絡，700 s之后,，仿真設置為對GPS信號失鎖,，濾波算法采用訓練好的神經(jīng)網(wǎng)絡，所得到的速度誤差如圖5,、圖6,、圖7所示。

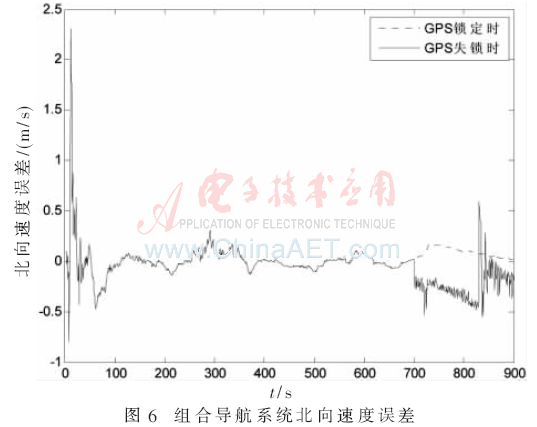
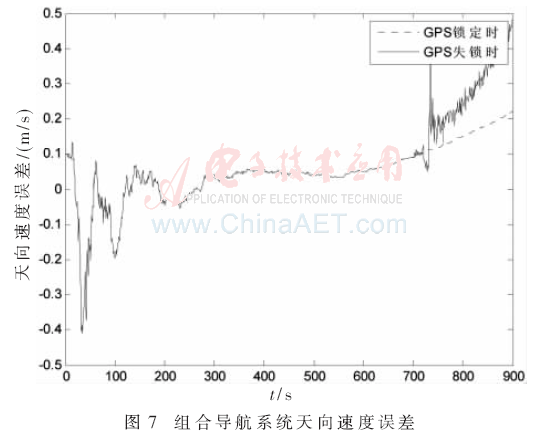
    通過速度誤差分析不難發(fā)現(xiàn)：衛(wèi)星失鎖后,，東向速度最大誤差小于0.5 m/s,，北向速度誤差也小于1 m/s，天向速度誤差也小于0.5 m/s,，采用神經(jīng)網(wǎng)絡輔助方法濾波的速度誤差幾乎能比擬在衛(wèi)星鎖定時的速度誤差,。各個方向的速度誤差與純慣導的速度誤差相比有較大改善，充分證明了算法的有效性,。

    通過仿真進一步得到組合導航的經(jīng)度誤差,、緯度誤差以及高度誤差，如圖8,、圖9,、圖10所示。

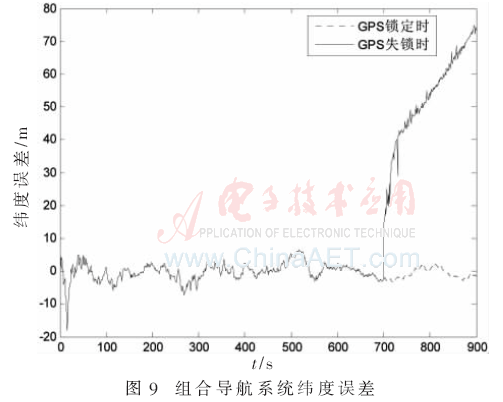
    從仿真結果看,，經(jīng)度最大誤差優(yōu)于70 m,，緯度最大誤差優(yōu)于80 m，高度最大誤差優(yōu)于20 m,。經(jīng)度和緯度的仿真誤差較GPS鎖定時稍差,，但短時間內(nèi)可以滿足實際精度需求。BP神經(jīng)網(wǎng)絡輔助的組合導航系統(tǒng)濾波算法相比于純慣導系統(tǒng)的位置誤差,，精度提高較大,。

5 結論

    通過仿真驗證，證實了在短時間內(nèi),，基于BP神經(jīng)網(wǎng)絡輔助的GPS/INS組合導航系統(tǒng)濾波算法的有效性,，能夠在組合導航系統(tǒng)對GPS衛(wèi)星失鎖的條件下，極大地改善組合導航系統(tǒng)精度,。但若是GPS信號長期失鎖,，采用該濾波方法,，組合導航系統(tǒng)的精度得不到保證。然而,，在實際應用中,，GPS信號不可能長時間失鎖，仿真中所采用的時段基本能夠滿足要求,，因此,，本文所述方法具有一定的實際意義。

參考文獻

[1] 秦永元.卡爾曼濾波與組合導航原理[M].西安：西北工業(yè)大學出版社,，2007.

[2] 陳燃,，劉繁明.基于BP神經(jīng)網(wǎng)絡對INS/GPS組合導航數(shù)據(jù)融合技術的研究[D].哈爾濱：哈爾濱工程大學，2009.

[3] 嚴恭敏,，秦永元.捷聯(lián)慣導算法及車載組合導航系統(tǒng)研究[D],，西安：西北工業(yè)大學，2004.

[4] 崔留爭.神經(jīng)網(wǎng)絡輔助卡爾曼濾波在組合導航中的應用[J].光學精密工程,，2014,，22(5).

[5] 張敏虎，任章.神經(jīng)網(wǎng)絡輔助高動態(tài)GPS/INS組合導航融合算法[C].Proceedings of the 27th Chinese Control Conference July 16-18,，2008,，Kunming Yunnan，China.

[6] 林雪原,，鞠建波.利用神經(jīng)網(wǎng)絡預測的GPS/SINS組合導航系統(tǒng)算法研究[J].武漢大學學報信息科學版,，2011，36(5).

[7] 耿世松,，裴?？。奁竭h.基于神經(jīng)網(wǎng)絡輔助觀測的連續(xù)組合導航算法研究[J].高技術通訊,，2009,，19(1).