引言

　　三軸陀螺儀常用來測量物體三個方向的角速率信息,，及估計設(shè)備姿態(tài)信息。相對于傳統(tǒng)陀螺儀,，采用MEMS集成制造工藝的陀螺儀具有重量輕,、體積小、成本低,、可靠性高等優(yōu)點，在機載導(dǎo)航及車載導(dǎo)航等領(lǐng)域得到了廣泛應(yīng)用,。系統(tǒng)姿態(tài)測量的精度除了與姿態(tài)解算算法有關(guān)外,，還與MEMS陀螺儀的加工工藝及安裝精度相關(guān)。因而,，對MEMS陀螺儀誤差估計和標(biāo)定的研究具有重要意義[1-2],。

　　陀螺儀的標(biāo)定方法主要有基于轉(zhuǎn)臺的多位置角速率試驗標(biāo)定方法[3]和現(xiàn)場多位置標(biāo)定方法[4-5]。傳統(tǒng)的標(biāo)定方法以高精度轉(zhuǎn)臺為測試基礎(chǔ),，標(biāo)定過程非常復(fù)雜?，F(xiàn)場標(biāo)定能夠降低工作量，但標(biāo)定精度相對較差,。文獻(xiàn)[6]在陀螺速率試驗和24位置實驗的基礎(chǔ)上,，提出一種無需基準(zhǔn)北向的陀螺標(biāo)定方法，消除了不對北誤差影響,。文獻(xiàn)[7,，8]結(jié)合傳統(tǒng)的靜態(tài)多位置和速率標(biāo)定方法，提出基于雙軸旋轉(zhuǎn)機構(gòu)的6位置標(biāo)定方法,，該方法求解標(biāo)度因子和安裝誤差較為方便,，但在求解常值漂移時步驟繁瑣。文獻(xiàn)[9]分別采用24位置,、12位置和8位置對陀螺儀進(jìn)行標(biāo)定試驗,，表明標(biāo)定位置減少，能夠降低標(biāo)定成本,，但標(biāo)定精度隨之降低,。因而要探究有效的標(biāo)定位置，在降低標(biāo)定成本的同時提高標(biāo)定精度,。

　　本文對陀螺儀的誤差源進(jìn)行分析,，建立了測量誤差的數(shù)學(xué)模型，提出了一種新型4位置陀螺儀標(biāo)定方法,，補償了零偏,，安裝誤差及標(biāo)度因子對陀螺儀的影響,，并進(jìn)行相關(guān)實驗測試。測試結(jié)果表明,，該方法簡化了現(xiàn)有標(biāo)定步驟,，節(jié)約了標(biāo)定時間；標(biāo)定結(jié)果滿足預(yù)期試驗要求,，標(biāo)定方法合理,、可行。

1 陀螺儀的誤差模型

　　在三軸陀螺儀中,，三個軸向的陀螺分別安裝于三個正交面上,，構(gòu)成右手坐標(biāo)系。由于陀螺儀自身工作原理,、結(jié)構(gòu),，以及集成制造、安裝等因素影響,，導(dǎo)致陀螺儀的輸入軸坐標(biāo)系之間不能正交,，存在一定的安裝誤差。陀螺儀標(biāo)定的目的就是補償輸出值與測量值之間的偏差,，補償測量值為零而實際輸出值不為零的零偏,，補償由加工精度、裝配工藝等原因引起的安裝耦合誤差,，因此MEMS陀螺的輸出模型可以表示為：

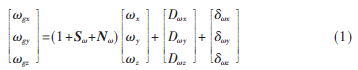
　　其中,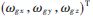，為敏感軸測量的角速度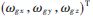，為真實角速度,，?啄?棕為線性刻度因子誤差矢量,，N為非正交因子矢量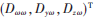，為常值漂移(零偏),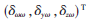，為陀螺噪聲誤差,。考慮到陀螺噪聲誤差對標(biāo)定結(jié)果的影響較小,，忽略噪聲誤差對測量結(jié)果影響,。令K=1+S+N，則上述公式可以變換為：

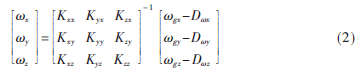
　　其中,，Ky x,、Kz x為敏感軸x對應(yīng)的安裝誤差耦合系數(shù)；Kx y,、Kz y為敏感軸y對應(yīng)的安裝誤差耦合系數(shù),；Kx z、Ky z為敏感軸z對應(yīng)的安裝誤差耦合系數(shù),；Kx x,、Ky y ,、Kz z 為3個敏感軸對應(yīng)的標(biāo)定因數(shù)；D x ,、D y ,、D z是陀螺敏感軸x、y,、z的常值漂移(零偏),。

2 4位置標(biāo)定方案

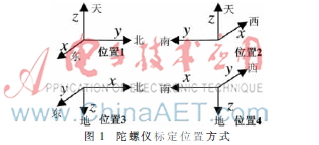
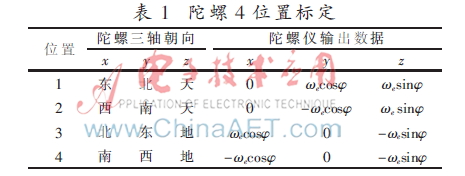
　　為了標(biāo)定陀螺儀的標(biāo)度因數(shù)和安裝誤差，需要進(jìn)行標(biāo)定試驗,。由文獻(xiàn)[6]可知,，三軸陀螺儀在東北天坐標(biāo)系中共有24種位置。為了減少標(biāo)定狀態(tài),，使陀螺的敏感軸指向東向或西向,，則地球自轉(zhuǎn)速率在該軸向的分量為零。依此原則,，從24個狀態(tài)中優(yōu)選出4個狀態(tài)進(jìn)行陀螺標(biāo)定。將陀螺儀旋轉(zhuǎn)至如圖1所示位置,，陀螺儀在上述4個位置的理想輸出如表1所示,。具體方法如下：在三維轉(zhuǎn)臺上記錄一段時間內(nèi)軸向陀螺在每一位置的輸出數(shù)據(jù)。當(dāng)某一個位置采樣結(jié)束后,，轉(zhuǎn)動試驗臺至另一位置繼續(xù)完成上述試驗,，依次進(jìn)行4個位置的試驗。根據(jù)不同位置獲取的數(shù)據(jù)標(biāo)定陀螺的零偏,、標(biāo)度因數(shù)和安裝誤差,。

　　2.1 陀螺儀零偏估算

　　分別求上述4位置陀螺輸出數(shù)據(jù)的平均值xi，則陀螺的零偏為：

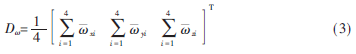
　　2.2 標(biāo)度因數(shù)估算

　　陀螺在位置1的理想輸入和輸出分別為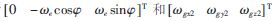,，在位置2的理想輸入和輸出分別為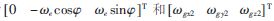,，其中We為地球自轉(zhuǎn)角速率，為當(dāng)?shù)氐乩砭暥?，由?1)可知,，陀螺在位置1和位置2的測量值分別為：

　　陀螺在位置3的理想輸入和輸出，在位置4的理想輸入和輸出,，由式(1)可知,，陀螺在位置3和位置4的測量值分別為：

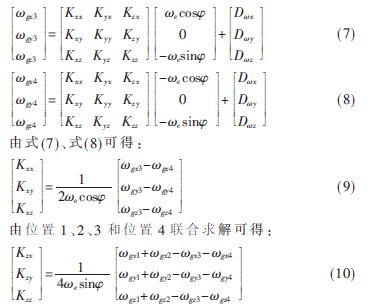
3 陀螺儀標(biāo)定實驗結(jié)果

　　利用上述標(biāo)定方法，將陀螺儀安裝于三軸轉(zhuǎn)臺內(nèi)框的固定板上,，使陀螺的敏感軸x,、y、z軸與轉(zhuǎn)臺的三個轉(zhuǎn)動軸平行,。利用數(shù)據(jù)記錄模塊接收高速率的陀螺儀輸出數(shù)據(jù)幀,，并將數(shù)據(jù)幀寫入SD卡,。待實驗結(jié)束后，從SD卡中讀出數(shù)據(jù)幀并解算陀螺參數(shù),，進(jìn)行陀螺儀標(biāo)定,。經(jīng)標(biāo)定實驗后，陀螺儀的標(biāo)定因數(shù)矩陣和零偏分別為：

　　轉(zhuǎn)臺以30°/s的角速率分別繞x軸,、y軸和z軸旋轉(zhuǎn)5 min,，利用數(shù)據(jù)記錄模塊獲取陀螺儀輸出的三軸角速率數(shù)據(jù)，對陀螺儀輸出的三軸角速率數(shù)據(jù)進(jìn)行分析,。標(biāo)定補償前陀螺儀三軸輸出數(shù)據(jù)為[29.821 441  29.853 325  29.761 518],，標(biāo)定補償后提高到[29.968 197  29.930 426  29.967 598]，標(biāo)定前,、后誤差分析如表2所示,。由分析可知陀螺儀標(biāo)定補償后輸出精度比補償前提高約1個數(shù)量級。

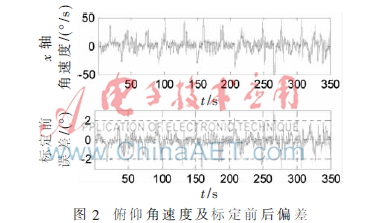
　　將標(biāo)定后的陀螺儀應(yīng)用于某小型飛行控制,，進(jìn)行相關(guān)飛行試驗,。圖2為飛行過程中俯仰角速率標(biāo)定后的試驗曲線和標(biāo)定前、后之間偏差曲線,；圖3為飛行過程中滾轉(zhuǎn)角速率標(biāo)定后的試驗曲線和標(biāo)定前,、后之間偏差曲線；圖4為飛行過程中偏航角速率標(biāo)定后的試驗曲線和標(biāo)定前,、后之間偏差曲線,。

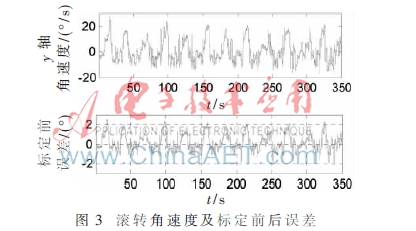
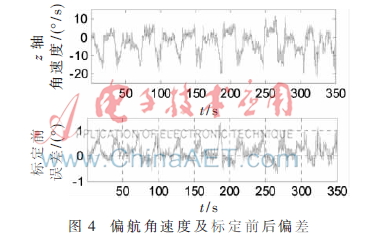
　　從圖中可以看出：x軸陀螺儀輸出數(shù)據(jù)范圍集中為(-40  40)，標(biāo)定補償?shù)慕嵌确秶鸀?-2  2),；y軸陀螺儀輸出數(shù)據(jù)范圍為(-20  20),，標(biāo)定補償?shù)慕嵌确秶鸀?-1.5  2)；z軸陀螺儀輸出數(shù)據(jù)范圍為(-20  10),，標(biāo)定補償?shù)慕嵌确秶鸀?-0.5  1),。

　　從實際試驗結(jié)果可知，采用本文提出的4位置姿態(tài)標(biāo)定算法,，陀螺儀的安裝誤差,、零偏和標(biāo)度因子能得到有效補償，補償后陀螺儀輸出參數(shù)解算的飛行器姿態(tài)更符合實際飛行姿態(tài),。

4 結(jié)論

　　本文針對低成本陀螺儀存在零偏,、標(biāo)度因數(shù)和安裝誤差角等問題，建立了陀螺儀誤差模型,，提出了4位置標(biāo)定方法,，并將該方法應(yīng)用于陀螺儀進(jìn)行標(biāo)定，給出了標(biāo)定后測試結(jié)果，簡化了標(biāo)定過程,，提高了標(biāo)定精度,，驗證了該補償方法的正確性和有效性。

　　參考文獻(xiàn)

　　[1] 范建英,，李杰,，陳文蓉，等.高精度數(shù)字陀螺儀安裝誤差標(biāo)定與補償方法[J].傳感技術(shù)學(xué)報,，2013(4)：525-529.

　　[2] 彭孝東,，陳瑜，李繼宇,，等.MEMS三軸數(shù)字陀螺儀標(biāo)定方法研究[J].傳感器與微系統(tǒng),，2013(6)：63-65.

　　[3] ARTESE G，TRECROCI A.Calibration of a low cost MEMSINS sensor for an integrated navigation system[C].The 21stISPRS,，2008：877-882.

　　[4] AYDEMIR G A,，SARANLL A.Characterization and calibra-tion of MEMS inertial sensors for state and parameter esti-mation applications[J].Measurement，2012,，45(5)：1210-1225.

　　[5] SCHOPP P,，KLINGBEIL L，PETERS C,，et al.Sensor fusion algorithm and calibration for a gyroscope-free IMU[J].Pro-cedia Chemistry,，2009，1(1)：1323-1326.

　　[6] FU L,，ZHU Y,，WANG L,，et al.A D-optimal multi-posi-tion calibration method for dynamically tuned gyroscopes[J].Chinese Journal of Aeronautics,，2011，24(2)：210-218.

　　[7] 吳旭,，孫楓,，陳軍.FOG雙軸旋轉(zhuǎn)六位置現(xiàn)場標(biāo)定方法[J].傳感器與微系統(tǒng)，2012(9)：50-53.

　　[8] 孫楓,，孫偉.基于雙軸轉(zhuǎn)位機構(gòu)的光纖陀螺標(biāo)定方法[J].控制與決策,，2011，26(3)：346-350.

　　[9] FU L,，YANG X,，WANG L L.A novel calibration procedurefor dynamically tuned gyroscope designed by D-optimal approach[J].Measurement，2013,，46(9)：3173-3180.