0 引言

    多天線多輸入多輸出(Multiple Input and Multiple Output，MIMO)技術及其應用已成為當今移動通信技術中最重要的研究領域之一,，MIMO無線通信技術可以顯著提高無線傳輸系統(tǒng)的性能^[1],，MIMO系統(tǒng)是增大帶寬效率的有效方法^[2]。MIMO系統(tǒng)頻譜效率通過同時在相同的頻率信道發(fā)送不同的天線及信號得到,，并使用多個接收天線和相應的接收算法來實現(xiàn)^[3],。由于系統(tǒng)采用多發(fā)射天線和多接收天線，所述多個二維統(tǒng)計特性對MIMO系統(tǒng)有著最重要的意義^[6],。最近公布的眾多研究工作都量化了這個MIMO系統(tǒng)的潛在性能,，考慮將不同類型的天線調(diào)校放置在各種環(huán)境中^[3]。建模過程中由于散射體的隨機分布導致了信道參數(shù)估計的復雜性,，根據(jù)文獻[3]所述仍然缺乏一個簡單而準確的相關模型,。

    本文主要是為MIMO系統(tǒng)介紹均勻線性陣列（Uniform Linear Array，ULA）,、均勻圓陣（Uniform Circular Array,，UCA）在拉普拉斯分布下的簡單空間相關性模型^[4]，推導出波達信號在拉普拉斯分布下的衰落相關性解析公式,，并分析兩種線性陣列下的接收信號相關性及其影響因素,。文獻[5]給出了MIMO系統(tǒng)信道容量的計算公式。本文利用衰減因子α,、陣元間距,、中心到達角（Angle of Arrival，AOA）,、信噪比等參數(shù)分析兩種天線陣列下的系統(tǒng)信道容量,，并比較ULA與UCA對于MIMO系統(tǒng)信道容量的影響。

1 拉普拉斯分布下空間衰落相關性

1.1 線性天線陣列MIMO空間衰落相關性

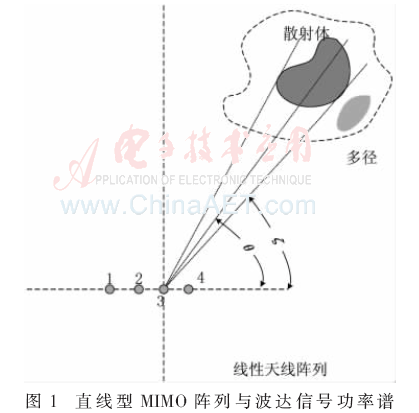
式中,，d和m分別表示天線間距和陣列天線陣元數(shù)目,。因此陣元m和n的空間相關性可以表示為^[7]：

其中，a是拉普拉斯分布函數(shù)衰減因子,，其大小與角度擴展相關,，K是分布密度函數(shù)歸一化常數(shù)，本文中可假設K值為1,，ζ是平均到達方向角,。隨著a的增加，角度擴展減小,。

    將式(4)代入式(3)中,，經(jīng)推導和變換可得到線性天線陣列下拉普拉斯分布的空間衰落相關性公式：

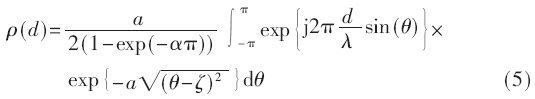
1.2 圓形天線陣列MIMO空間衰落相關性

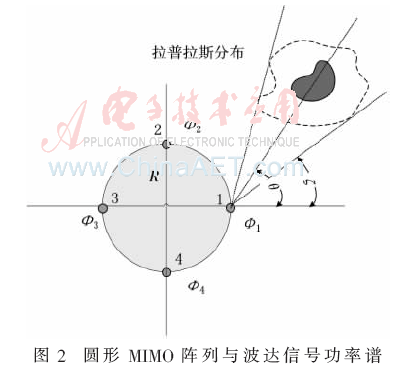
    其中:

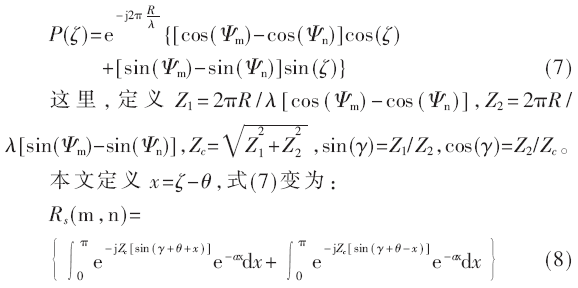
2 MIMO多天線系統(tǒng)信道容量

    在移動通信系統(tǒng)中信道容量在根本上決定了無線系統(tǒng)性能,，許多文獻研究了IID復高斯信道模型, 奠定了信道容量分析的理論基礎^[8]。假設發(fā)射端不具有信道信息, 則發(fā)射功率將均勻分配在每個發(fā)射元上, 此時一個突發(fā)時間內(nèi)信道容量的統(tǒng)計均值為：

    根據(jù)詹森不等式^[9]Elogx≤logEx和log₂|·|的容量,，式(9)平均容量可設置界限為：

3 數(shù)值結果與分析

    根據(jù)式(5),、式(8)仿真得到圖3、圖4,。圖3,、圖4分別表示線性陣列和圓形陣列拉普拉斯分布在不同衰減因子值情況下空間衰落相關性與陣元間距的關系。從圖3可以發(fā)現(xiàn),，當衰減因子a為固定值時,，隨著陣元之間距離的增加，空間相關性呈現(xiàn)下降趨勢,。圖4中,，衰落相關性隨著R的增加而減小。隨著a的增加(即角度擴展減小),，衰落相關性增加,。

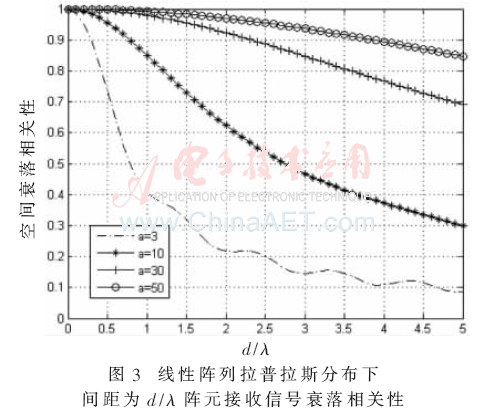
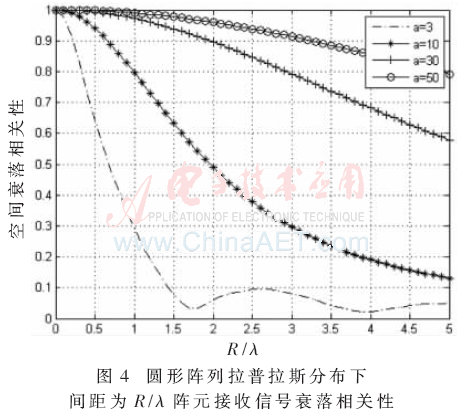
    圖5是當d/λ和θ為固定值時，線性陣列拉普拉斯分布下MIMO系統(tǒng)信道容量在衰減因子a為不同值時與信噪比SNR的關系,。從圖中可以發(fā)現(xiàn)隨著信噪比SNR的增大,，信道容量逐漸增大。圖5中取衰減因子a三個不同的值,，衰減因子a越小時信道容量越大。

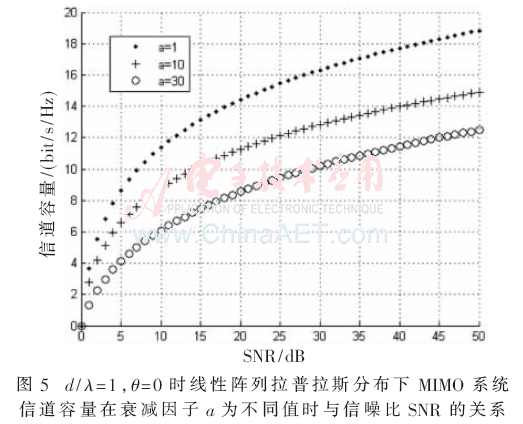
    圖6是a=30,，θ=0為固定值時線性陣列拉普拉斯分布下MIMO系統(tǒng)信道容量在R/?姿為不同值時與信噪比SNR的關系,。從圖6可以推導出結論，隨著參數(shù)d/λ的增加,，線性MIMO系統(tǒng)的容量更高,。

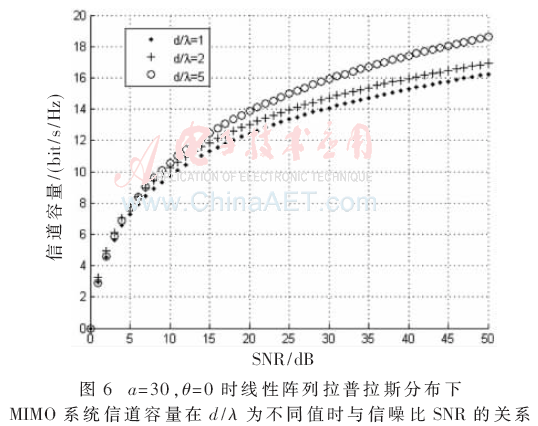
    圖7所示為當R/λ和θ為固定值時，圓形陣列拉普拉斯分布下衰減因子a為不同值時信噪比SNR對MIMO系統(tǒng)信道容量的影響,。同樣,，如在圖5中看到的，衰減因子a越小時信道容量越大,，衰減因子a減小,，角度擴展增大，空間相關性隨之減小,，信道容量隨之增大,。

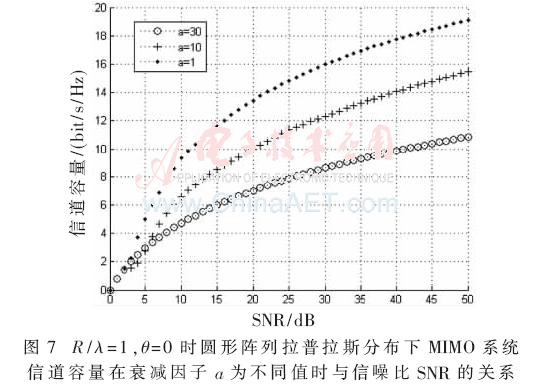
    圖8是a=30、θ=0為固定值時圓形陣列拉普拉斯分布下R/λ為不同值時信噪比SNR對MIMO系統(tǒng)信道容量的影響,。結合圖8可以發(fā)現(xiàn)R/λ值越大時MIMO系統(tǒng)的信道容量更高,，這與線性陣列下分析的結果是相同的,，R/λ增加意味著天線間距離增大，天線之間的相關性會減小,，所以系統(tǒng)信道容量會增大,。

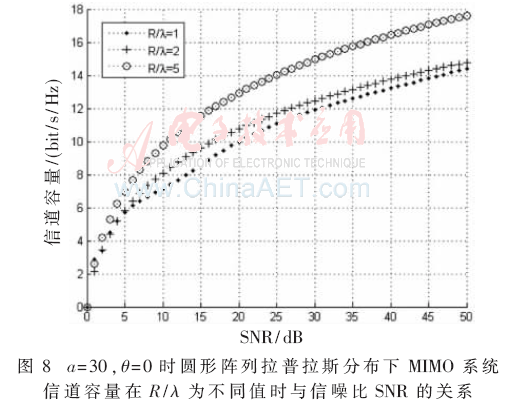
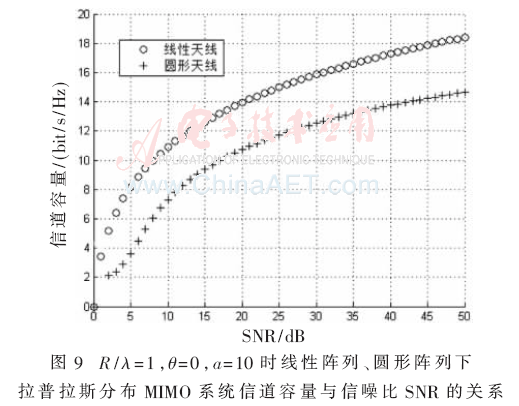
    圖9是R/λ=1，θ=0,，a=10時在SNR為不同值時,，線性陣列與圓形陣列下拉普拉斯分布MIMO系統(tǒng)信道容量的比較。從圖9中可以明顯發(fā)現(xiàn),，當參數(shù)a,、R或者d、θ全部為定值時,，系統(tǒng)信道容量隨著信噪比SNR的增加而增加,，當SNR為取某一值時，圓形陣列下的系統(tǒng)信道容量比線性陣列下的更高,。因此可以得出結論拉普拉斯分布在參數(shù)為定值情況下,，UCA比ULA更具優(yōu)勢，可以更好地提高系統(tǒng)性能,。

4 結論

    本文主要是為MIMO系統(tǒng)介紹均勻線性陣列,、均勻圓陣在拉普拉斯分布下的空間相關性模型，推導了波達信號在拉普拉斯分布下的相關性解析公式,，并利用衰減因子a,、陣元間距、AOA,、信噪比等參數(shù)來分析,，比較ULA與UCA對于MIMO系統(tǒng)性能的影響。分析結果發(fā)現(xiàn)衰減因子a減小,，角度擴展隨之增大,，空間衰落相關性減小，這使得MIMO系統(tǒng)信道容量增加,，提高了無線信道多天線MIMO系統(tǒng)性能,。同樣，半徑R增加使得空間相關性增加,，系統(tǒng)信道容量也隨之增加,。在線均勻陣ULA與均勻圓陣UCA對于MIMO系統(tǒng)信道容量的比較中，UCA比ULA更具優(yōu)勢,，可以更好地提高系統(tǒng)信道容量,。

參考文獻

[1] JAKES W C.Microwave mobile communications[M]．New York：Wiley，1974.

[2] MOLISCH A F,，WIN M Z.MIMO systems with antenna selection[J].Microwave Magazine,，IEEE,，2004，5(1)：46-56.

[3] LOYKA S L.Channel capacity of MIMO architecture using the exponential correlation matrix[J].Communications Letters,，IEEE,，2001，5(9)：369-371.

[4] TSAI J A,，WOERNER B D.The fading correlation function of a circular antenna array in mobile radio environment[C].GlobalTele Communications Conference,，2001.GLOBECOM′01.IEEE.IEEE，2001,，5：3232-3236.

[5] HANLEN L,，GRANT A.Capacity analysis of correlated MIMO channels[D].IEEE，2003.

[6] JAKES W C.Microwave mobile communications[M].New York：Wiley Inter science,，1974.

[7] 陳靖峰,，周杰.角能量分布及互耦效應對MIMO天線系統(tǒng)性能影響的研究[D].南京：南京信息工程大學圖書館，2012.

[8] KAFLE P L,，INTARAPANICH A,，SESAY A B，et al.Spatial correlation and capacity measurements for wideband MIMO channels in indoor office environment[J].Wireless Communications,，IEEE Transactions on,，2008，7(5)：1560-1571.

[9] LOYKA S,，KOUKI A.On the use of Jensen's inequality for MIMO channel capacity estimation[C].Electrical and Computer Engineering,，2001.Canadian Conference on.IEEE，2001,，1：75-480.