0 引言

　　高復(fù)雜度、樣本數(shù)據(jù)規(guī)模的持續(xù)增長是時間序列的兩大特點[1],。時間序列預(yù)測算法是從傳統(tǒng)的以ARIMA模型為核心的線性預(yù)測算法發(fā)展到以機(jī)器學(xué)習(xí)算法為核心的非線性預(yù)測算法,。線性預(yù)測算法能夠以較低的計算復(fù)雜度獲得較為理想的運(yùn)算結(jié)果，非線性預(yù)測算法能夠很好地逼近任意復(fù)雜度的非線性函數(shù),。而組合預(yù)測算法針對同一時間序列，結(jié)合線性和非線性模型的優(yōu)點,，可以獲得更佳預(yù)測效果,。

　　組合預(yù)測方法由J.M.Bates和C.WJ.Granger在1969年首次提出，并廣泛應(yīng)用于各個領(lǐng)域,。如ARIMA模型和SVM算法的組合在預(yù)測股票走勢時,，預(yù)測精度與單一模型相比有明顯提高[2]。利用粒子群算法優(yōu)化的BP神經(jīng)網(wǎng)絡(luò)的學(xué)習(xí)算法,，結(jié)合ARIMA和GM灰色預(yù)測的三個模型的組合預(yù)測也證明了其有效性與精確性[3-4],。ARIMA和BP的組合方案被應(yīng)用于海洋流速、城市交通客流量的預(yù)測中[5-6],。

　　時間序列預(yù)測屬于對時間序列規(guī)律的總結(jié)歸納,，是犯罪數(shù)據(jù)挖掘的重要應(yīng)用之一[7-8]。在犯罪預(yù)測領(lǐng)域，國內(nèi)外學(xué)者進(jìn)行了一系列研究,。如對犯罪預(yù)測的研究方法的探索[9],；通過相空間重構(gòu)針對時間序列進(jìn)行重構(gòu)，并使用基于粒子群(Particle Swarm Optimized,，PSO)優(yōu)化的最小二乘支持向量機(jī)LSSVM建立犯罪趨勢預(yù)測模型[10],；使用SVD算法對犯罪時間序列進(jìn)行分解及預(yù)測[11]等，但單一模型預(yù)測的精度還有待改善,?；诖耍绾螌Ψ缸飼r間序列進(jìn)行精確和高效的預(yù)測成為一個重要的研究課題,。本文提出的混合模型利用ARIMA,、LSSVM和組合預(yù)測法的優(yōu)勢，對微軟公共犯罪數(shù)據(jù)集進(jìn)行建模與預(yù)測,。通過仿真實驗得出結(jié)論,，ARIMA-LSSVM混合模型與常用的ARIMA-BP混合模型相比，預(yù)測精確度有明顯提高,。

1 時間序列預(yù)處理-相空間重構(gòu)

　　對于高維時間序列數(shù)據(jù),，在建模之前需對序列預(yù)先進(jìn)行相空間重構(gòu)PSR處理。

　　首先對長度為N的原始時間序列Xt={x1,，x2,，…，xN}進(jìn)行處理,，得到延遲序列Y(t)：

　　其中,，?子稱為延遲算子或采樣算子，m稱為嵌入的維度,。

　　然后建立Y(t)到Y(jié)(t+T)的映射函數(shù)關(guān)系：

　　YF(t+T)=f(Y(t))+et(2)

　　其中,，Y(t)為原始序列，YF(t+T)為預(yù)測序列,，et為典型噪聲因子,。

　　由式(2)可得：

　　因此預(yù)測結(jié)果可以表示為：

　　其中，x為t+T+(m-1)子時刻時間序列的取值,。由式(3)和式(4)可知,，YF(t+T)中包含主要預(yù)測結(jié)果。

　　2 ARIMA模型

　　ARIMA(Autoregressive Integrated Moving Average Model)模型表達(dá)式為ARIMA(p,，d,，q)。其中d代表差分次數(shù),，p和q分別代表自回歸和移動平均系數(shù),。

　　模型定義如下：

　　引入延遲算子(B)：

　　模型簡化為：

　　若xt為非平穩(wěn)序列,，通過差分得到平穩(wěn)序列zt：

　　其中，d為差分次數(shù),。

　　3 LSSVM模型

　　最小二乘支持向量機(jī)LSSVM 是結(jié)構(gòu)最小化風(fēng)險函數(shù)為二次損失函數(shù)的支持向量機(jī),。

　　支持向量機(jī)分類器的表達(dá)式為：

　　其中，k=1,，…,，N；?棕為權(quán)重值,，b為結(jié)構(gòu)風(fēng)險規(guī)則,。xk為輸入模式，yk為輸出,。?準(zhǔn)為將輸入數(shù)據(jù)映射到高維特征空間的非線性映射,。?著k為誤差變量。

　　對于最小二乘支持向量機(jī),，基于結(jié)構(gòu)風(fēng)險最小化原則,，優(yōu)化問題為：

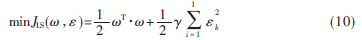
　　其中，?酌>0,，為正則化參數(shù),。

　　根據(jù)Karush-Kuhn-Tucker(KKT)條件和Mercer條件，LSSVM的優(yōu)化問題轉(zhuǎn)化為求解線性方程,，最后得到方程：

　　LSSVM的核函數(shù)徑向基RBF核：

　　其中,，?滓為核寬度。RBF內(nèi)核適用于大多數(shù)預(yù)測問題,，且效率高,，處理速度快。使用粒子群優(yōu)化算法PSO優(yōu)化的LSSVM比傳統(tǒng)LSSVM具有更好的分類效果[12],。

　　4 ARIMA-LSSVM混合模型

　　混合模型包括一個線性模型和一個或多個非線性模型,。混合模型Zt可以表示為：

　　Ht=Lt+Nt(13)

　　其中,，Lt和Nt分別為混合模型的線性和非線性成分,。

　　首先由線性模型ARIMA得出序列預(yù)測值t，與原序列值相減計算得到預(yù)測殘差?著t：

　　然后用非線性模型LSSVM對殘差序列進(jìn)行建模：

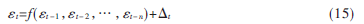
　　其中,，f(·)為非線性函數(shù)，?著t-n為t-n時刻的殘差,，?駐t為隨機(jī)誤差,。

　　最后，殘差序列經(jīng)過非線性模型修正后得到t,，相加得到最終結(jié)果：

　　Granger的實驗證明混合模型要取得最優(yōu)預(yù)測效果,，成員模型應(yīng)該是次優(yōu)的[13],。ARIMA模型在短期預(yù)測中預(yù)測誤差較小[14]，混合模型首先利用ARIMA獲取較為精確的預(yù)測序列,，與原序列相減得到殘差序列,。殘差序列對應(yīng)于ARIMA無法解釋的非線性規(guī)律，然后使用LSSVM模型對非線性部分進(jìn)行建模與預(yù)測,。最后將兩部分的結(jié)果相加得到混合模型最終預(yù)測結(jié)果,。算法框架圖如圖1所示。

　　5 實驗

　　5.1 數(shù)據(jù)集

　　實驗數(shù)據(jù)集為1993年~2009年美國警方記錄在案的犯罪數(shù)據(jù)[15],，實驗環(huán)境為SPSS16.0和MatlabR2011a,。

　　5.2 預(yù)測模型的評判標(biāo)準(zhǔn)

　　使用如下統(tǒng)計量檢驗?zāi)Ｐ偷臄M合效果和預(yù)測效果：

　　其中，Zt,、t分別為真實值和預(yù)測值,。MSE和MAPE分別為均方誤差和平均絕對百分比誤差。n為預(yù)測樣本個數(shù),。eMSE和eMAPE值越小,表明模型的預(yù)測精度越高,。

　　5.3 預(yù)測模型的參數(shù)選擇

　　ARIMA模型的參數(shù)根據(jù)自相關(guān)函數(shù)圖ACF和偏自相關(guān)函數(shù)圖PACF進(jìn)行選擇。LSSVM模型使用RBF核函數(shù)和二維柵格搜索方法尋找最優(yōu)核參數(shù),。BP神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)設(shè)置為3-10-5-1,。

　　5.4 實驗方案

　　首先對模型ARIMA、GM,、BP,、LSSVM進(jìn)行時間序列建模，計算其預(yù)測誤差,，結(jié)果見表1,。

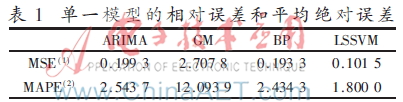
　　結(jié)果表明，ARIMA,、BP,、LSSVM 3種算法的誤差較小。綜合建模和預(yù)測效果,，選取ARIMA,、LSSVM、BP作為對比模型,。

　　然后使用本文提出的 ARIMA-LSSVM 混合模型進(jìn)行預(yù)測,，預(yù)測的結(jié)果對比如圖2所示。橫坐標(biāo)表示時間序列的序列號K,，縱坐標(biāo)表示對應(yīng)時刻的犯罪數(shù)據(jù),。K=12，13,，14時曲線對應(yīng)于2007～2009年的預(yù)測值,。算法預(yù)測參數(shù)對比見表2,。

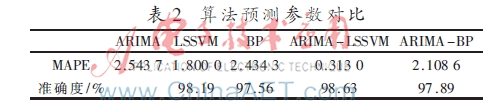
　　實驗結(jié)果表明，ARIMA-LSSVM對犯罪時間序列的預(yù)測誤差 MAPE遠(yuǎn)小于其他預(yù)測模型,預(yù)測準(zhǔn)確度也較高,。由于單一的線性模型或者非線性模型預(yù)測具有不穩(wěn)定性,，而本文選取的模型充分考慮了時間序列的平穩(wěn)和非平穩(wěn)性，使預(yù)測容納更多隱含信息,，結(jié)合模型的優(yōu)勢,，大大提高了預(yù)測的穩(wěn)定性和精確性，預(yù)測的結(jié)果更有實際意義,。

6 結(jié)論

　　本文使用ARIMA-LSSVM混合模型對犯罪時間序列進(jìn)行組合預(yù)測,，結(jié)果表明與ARIMA-BP混合模型相比, 該模型對小樣本的犯罪時間序列具有更高的預(yù)測精度和有效性。本文屬于針對時間信息的歸納與推測,，而結(jié)合空間信息和時間信息的時空分析與預(yù)測更能體現(xiàn)犯罪數(shù)據(jù)之間的緊密聯(lián)系,，分析結(jié)果包含更多信息，是未來進(jìn)一步的研究方向,。

　　參考文獻(xiàn)

　　[1] 何書元.應(yīng)用時間序列分析[M].北京：北京大學(xué)出版社,，2004：185-229.

　　[2] Pai Pingfeng，Lin Chih-Sheng.A hybrid ARIMA and supportvector machines model in stock price forecasting[J].Omega,，2005,，33(6)：497-505.

　　[3] 崔吉峰，乞建勛,，楊尚東.基于粒子群改進(jìn)BP神經(jīng)網(wǎng)絡(luò)的組合預(yù)測模型及其應(yīng)用[J].中南大學(xué)學(xué)報：自然科學(xué)版,，2009，40(1)：190-194.

　　[4] 單銳,，王淑花,，李玲玲,等.基于ARIMA，BP神經(jīng)網(wǎng)絡(luò)與GM的組合模型[J].遼寧工程技術(shù)大學(xué)學(xué)報：自然科學(xué)版,，2012,，31(1)：118-122.

　　[5] 董世超.基于ARIMA-BP神經(jīng)網(wǎng)絡(luò)模型海流流速預(yù)測研究[J].中國科技信息，2014(2)：86-88.

　　[6] 劉杰.城市交通樞紐短期客流量的組合預(yù)測模型[J].交通信息與安全,，2014(2)：41-44.

　　[7] Fu Tak-chung.A review on time series data mining[C].Engineering Applications of Artificial Intelligence,，2011，24(1)：164-181.

　　[8] Yu Chung-Hsien.Crime forecasting using data mining techniques[C].Data Mining Workshops(ICDMW),，2011 IEEE11th International Conference on.IEEE,，2011：779-786.

　　[9] 黃超，李繼紅.犯罪預(yù)測的方法[J].江蘇警官學(xué)院學(xué)報,，2011,，26(1)：107-110.

　　[10] 王少軍.時間序列預(yù)測的可重構(gòu)計算研究[D].哈爾濱：哈爾濱工業(yè)大學(xué), 2012.

　　[11] JIANG Q，BARRICARTE J J S.A crime rate forecast and decomposition method[J].International Journal of Crimino-logy and Sociological Theory，2011,，4(2)：648-656.

　　[12] ALWEE R，SHAMSUDDIN S M,，SALLEHUDDIN R.Hybrid support vector regression and autoregressive integ-rated moving average models improved by particle swarm optimization for property crime rates forecasting with economic indicators[J].The Scientific World Journal,，2013(1)：951475.

　　[13] Yearly time series(1993-2012)，provided by Eurostat(website)[DB/CD].https：//datamarket.com/data/set/1c05/crimes-recorded-by-the-police#!ds=1c05!vwx=6:6fwj=3.6.a.11.19&display=l.

　　[14] 陳昌和,，李清海,，張衍國，等.爐排-循環(huán)床復(fù)合垃圾焚燒爐燃燒過程模型[J].清華大學(xué)學(xué)報(自然科學(xué)版),，2008,，48(5)：832-835.

　　[15] Yang Xiaoguang.An empirical study on stock price based on ARIMA model[C].International Conference on LogisticsEngineering，Management and Computer Science,，LEMCS,，2014：273-276.