摘 要: 傳統(tǒng)FCM聚類(lèi)算法存在初始聚類(lèi)中心較為敏感的問(wèn)題,易陷入局部最優(yōu)。針對(duì)此問(wèn)題,提出了基于密度權(quán)值和自適應(yīng)免疫系統(tǒng)的FCM算法(d-AIFCM)。算法在對(duì)Web用戶進(jìn)行聚類(lèi)分析的過(guò)程中,基于用戶群體之間的相似性,引入密度權(quán)值生成候選初始聚類(lèi)中心,采用自適應(yīng)免疫系統(tǒng)的原理確定初始聚類(lèi)中心,自動(dòng)生成最佳分類(lèi),解決傳統(tǒng)FCM算法對(duì)初始聚類(lèi)中心敏感的問(wèn)題。實(shí)驗(yàn)結(jié)果表明,d-AIFCM算法在收斂次數(shù)和聚類(lèi)效果方面較其他同類(lèi)算法有所提升。
關(guān)鍵詞: 初始聚類(lèi)中心;FCM;自適應(yīng)免疫算法;Web用戶聚類(lèi)
0 引言
在互聯(lián)網(wǎng)高速發(fā)展的時(shí)代,Web服務(wù)的方式趨于多元化,如何為不同需求的Web用戶提供個(gè)性化服務(wù)是當(dāng)前網(wǎng)絡(luò)服務(wù)的研究熱點(diǎn)。目前,多個(gè)研究小組通過(guò)對(duì)Web用戶進(jìn)行聚類(lèi)分析,研究用戶的行為、興趣等信息,從而為用戶提供個(gè)性化服務(wù)。在實(shí)際應(yīng)用中,用戶的興趣受多方面影響,采用FCM進(jìn)行聚類(lèi)分析能較客觀地反映現(xiàn)實(shí)世界。本文對(duì)傳統(tǒng)的FCM算法進(jìn)行改進(jìn),并將其應(yīng)用于Web用戶聚類(lèi)分析,具有一定的研究意義。
1 相關(guān)工作
FCM算法對(duì)初始化數(shù)據(jù)較敏感,易陷入局部最優(yōu)。針對(duì)該問(wèn)題有兩種解決辦法:一種是在聚類(lèi)過(guò)程中進(jìn)行全局隨機(jī)搜索,參考文獻(xiàn)[1]利用模擬退火算法擾動(dòng)當(dāng)前聚類(lèi)結(jié)果,擾動(dòng)結(jié)果以一定的概率被認(rèn)為是當(dāng)前的全局最優(yōu)解,但計(jì)算耗時(shí)長(zhǎng)。另一種是改善初始化條件,參考文獻(xiàn)[2]提出的FaiNet算法利用生物克隆免疫系統(tǒng)的原理對(duì)原始數(shù)據(jù)進(jìn)行初始化,但其初始抗體群是隨機(jī)生成的;參考文獻(xiàn)[3]利用參考區(qū)域獲取聚類(lèi)中心,算法的性能依賴于區(qū)域半徑的選取。本文引入密度權(quán)值,將自適應(yīng)免疫原理與FCM算法結(jié)合提出d-AIFCM算法,該算法可自動(dòng)生成最佳分類(lèi),解決了FCM算法對(duì)初始聚類(lèi)中心敏感的問(wèn)題,能夠最大程度找到全局最優(yōu)解。
2 算法設(shè)計(jì)
2.1 用戶興趣矩陣
設(shè)pj為網(wǎng)站頁(yè)面,ui為訪問(wèn)用戶,則ui對(duì)pj的興趣度Iij為:

其中,ω表示ui對(duì)pj的瀏覽次數(shù),Tijt表示ui第t次訪問(wèn)pj的瀏覽時(shí)間。
定義1 (用戶興趣矩陣)以pj為橫坐標(biāo),以u(píng)i為縱坐標(biāo),以Iij為矩陣元素構(gòu)造用戶興趣矩陣:
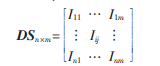
2.2 算法思路
設(shè)DS為樣本數(shù)據(jù)集合,D為樣本的密度權(quán)值;RS為候選初始聚類(lèi)中心集合;MS為初始聚類(lèi)中心集合。
2.2.1 確定候選聚類(lèi)中心
聚類(lèi)中心處于所代表類(lèi)的中心位置,且在樣本點(diǎn)密度連續(xù)的范圍內(nèi)應(yīng)該只具有一個(gè)聚類(lèi)中心,以防止兩個(gè)類(lèi)高度重疊。故聚類(lèi)中心的選取應(yīng)該滿足:具有較高的密度且與其他中心的距離盡可能大。
本文對(duì)每一個(gè)樣本點(diǎn)賦予密度權(quán)值:
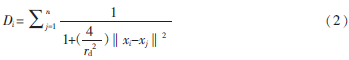
其中,‖xi-xj‖2為樣本點(diǎn)間的歐氏距離,rd表示領(lǐng)域密度半徑:
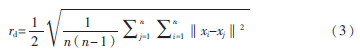
2.2.2 確定初始聚類(lèi)中心
自適應(yīng)免疫系統(tǒng)是人體的重要防御系統(tǒng)。當(dāng)機(jī)體受到抗原性異物刺激時(shí),被激活的抗體會(huì)發(fā)生選擇性克隆與變異,部分與抗原具有較高親和力的個(gè)體保存并組建成為該抗原的記憶細(xì)胞。受自適應(yīng)免疫系統(tǒng)的啟發(fā),抗體的克隆過(guò)程相當(dāng)于用戶興趣的傳播過(guò)程,變異過(guò)程相當(dāng)于用戶的興趣變化,記憶細(xì)胞類(lèi)似于聚類(lèi)中心。將RS中的元素Ri視為抗體,DS中的元素Gj視為抗原,產(chǎn)生的記憶細(xì)胞即為初始聚類(lèi)中心。
定義2 (親和度)親和度用來(lái)衡量抗體與抗原之間的匹配性,用τij表示:

定義3 (克隆)克隆是抗體進(jìn)行的自我復(fù)制過(guò)程,其克隆體的數(shù)量為:

定義4 (變異)變異是抗體在克隆過(guò)程中為增加個(gè)體多樣性而進(jìn)行的操作,變異公式如式(6)所示:
Ri=Ri-α(Ri-Gj)(6)
其中,α表示變異率,計(jì)算公式為:

其中,r為[0,1]之間的隨機(jī)數(shù),![[DY(`LHZM]FH)W]`][Z4_)D.png [DY(`LHZM]FH)W]`][Z4_)D.png](http://files.chinaaet.com/images/2015/08/07/6357457713829300009313298.png) ,DGj表示抗原Gj的密度權(quán)值。
,DGj表示抗原Gj的密度權(quán)值。
2.2.3 算法實(shí)施
d-AIFCM算法的具體實(shí)施過(guò)程如下:
(1)選取候選聚類(lèi)中心。
輸入:DS
輸出:RS
①初始化樣本密度權(quán)值D;
②選取擁有最大密度權(quán)值的樣本點(diǎn)xi,RS←xi,Set←xi,從DS中移除xi;
③選擇與xi最近的樣本點(diǎn)xl,Seti←xl,從DS中移除xl;
④選取xk,xk與Set中的樣本點(diǎn)距離最近;
⑤如果Dk小于Set中所有樣本點(diǎn)的密度權(quán)值,從DS中移除xk,轉(zhuǎn)到步驟④,否則轉(zhuǎn)至步驟②;
⑥輸出RS。
(2)確定初始聚類(lèi)中心。
輸入:DS,RS
輸出:MS
初始閾值σ、ε;
For Gj in DS;
If Gj與MS中的記憶細(xì)胞的距離大于ε;
計(jì)算RS中抗體Ri與抗原Gj的親和度;
選取親和度最大的前n個(gè)抗體→RS′;
For Ri in RS′
![`44%46O)1J03Z]LVHP2F}2H.jpg `44%46O)1J03Z]LVHP2F}2H.jpg](http://files.chinaaet.com/images/2015/08/07/6357457708621600007032826.jpg)
Rit=Ri-α(Ri-Gj)
End for
End for
計(jì)算Rit與Gj的親和度,按一定比例保留親和度較大的克隆體→MS′;
計(jì)算MS′中克隆體之間的歐式距離,刪除距離小于閾值σ的克隆體;
計(jì)算MS′的重心,得到記憶細(xì)胞M,M→MS;
End if
End for
(3)以MS中數(shù)據(jù)為初始聚類(lèi)中心執(zhí)行FCM算法的迭代過(guò)程。
3 實(shí)驗(yàn)結(jié)果與分析
3.1 實(shí)驗(yàn)數(shù)據(jù)與環(huán)境
實(shí)驗(yàn)數(shù)據(jù):實(shí)驗(yàn)數(shù)據(jù)采用某學(xué)院網(wǎng)站2012年1月份一周內(nèi)的Web日志,對(duì)Web日志進(jìn)行預(yù)處理,處理后共有2 786個(gè)用戶,28個(gè)網(wǎng)站頁(yè)面。
實(shí)驗(yàn)環(huán)境:Intel(R)Core(TM)[email protected] GHz CPU,4 GB內(nèi)存,Windows XP 32位操作系統(tǒng)。采用JAVA實(shí)現(xiàn)算法,并利用MATLAB制作實(shí)驗(yàn)圖表。
3.2 評(píng)價(jià)指標(biāo)
實(shí)驗(yàn)分別從迭代次數(shù)(I)、分支系數(shù)(PC)[4]和分配熵系數(shù)(PE)[5]對(duì)本文算法、原始的FCM算法以及參考文獻(xiàn)[3]的FaiNet算法進(jìn)行了比較分析。
PC值反應(yīng)了模糊集群之間成員共享的程度,值越高,集群之間的重疊就越小,計(jì)算公式為:

PE是驗(yàn)證模糊聚類(lèi)的另一個(gè)指標(biāo),值越小,算法就越穩(wěn)定,計(jì)算公式為:
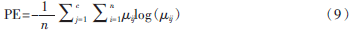
3.3 實(shí)驗(yàn)分析
在本實(shí)驗(yàn)中,F(xiàn)CM算法中的加權(quán)指數(shù)b取值為2,閾值σ取0.18~0.98共9個(gè)值,進(jìn)行9組實(shí)驗(yàn)。實(shí)驗(yàn)過(guò)程發(fā)現(xiàn),類(lèi)別數(shù)與σ相關(guān),σ越小,產(chǎn)生的記憶細(xì)胞數(shù)越多,類(lèi)別數(shù)越多,反之亦然,如圖1所示。
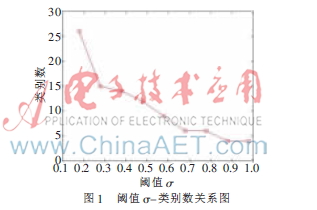
3.3.1 迭代次數(shù)的比較
FaiNet算法中的抗體群是隨機(jī)生成的,屬不完全匹配的記憶細(xì)胞法。d-AIFCM算法在進(jìn)行聚類(lèi)之前已經(jīng)充分考慮密度權(quán)值和距離等因素,又經(jīng)過(guò)克隆和變異操作,挑選出一批較精確的初始聚類(lèi)中心,類(lèi)別數(shù)也隨之確定,屬完全匹配記憶細(xì)胞法,避免了原始FCM算法隨機(jī)選取初始聚類(lèi)中心的弊端,這樣可以加快聚類(lèi)過(guò)程的收斂速度。可以通過(guò)實(shí)驗(yàn)來(lái)進(jìn)行驗(yàn)證,實(shí)驗(yàn)結(jié)果如圖2所示。
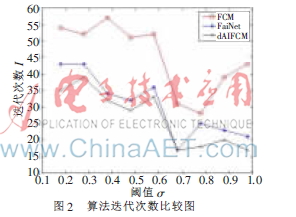
3.3.2 PC和PE的比較
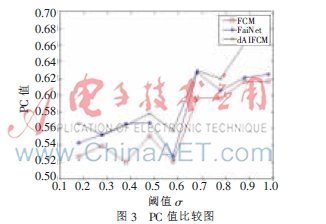
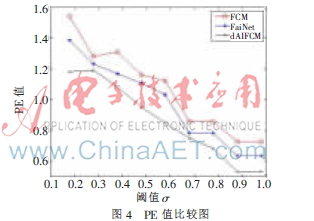
PC值和PE值的對(duì)比分別如圖3、圖4所示。從圖3及圖4可知,d-AIFCM算法具有較小的重疊性和較大的穩(wěn)定性。同時(shí),算法的PC值呈上升狀態(tài)最后趨于平穩(wěn),PE值呈下降狀態(tài)最后趨于平穩(wěn),說(shuō)明當(dāng)類(lèi)別數(shù)越多,針對(duì)用戶的分類(lèi)越詳細(xì),一個(gè)用戶所歸屬的類(lèi)別數(shù)也越多,則類(lèi)間的重疊性就會(huì)增加;當(dāng)類(lèi)別數(shù)越少,分類(lèi)結(jié)果趨于平穩(wěn),極端情況下,所有用戶同屬于一個(gè)類(lèi),則重疊性最小且最穩(wěn)定,但是這不符合實(shí)際情況,故在實(shí)際應(yīng)用中應(yīng)根據(jù)實(shí)際的需要選擇合適的σ值。
可以注意到,實(shí)驗(yàn)中閾值σ取不同的值時(shí),PC值的跳躍性較大,且PE值明顯均較高,這與數(shù)據(jù)集的特性有關(guān),數(shù)據(jù)集是從實(shí)際的Web日志中提煉出來(lái)的,數(shù)據(jù)稀疏性較大,可能影響算法的性能。
4 結(jié)論
本文針對(duì)FCM算法中存在的對(duì)初始聚類(lèi)中心敏感的問(wèn)題,在自適應(yīng)免疫算法的啟發(fā)下,提出了一種新的基于Web日志的聚類(lèi)方法。該方法無(wú)需人工作指定類(lèi)別數(shù),類(lèi)別數(shù)可在算法實(shí)施過(guò)程中自動(dòng)生成,并減輕了數(shù)據(jù)初始化對(duì)聚類(lèi)結(jié)果的影響。實(shí)驗(yàn)表明,該算法與相關(guān)算法相比,在收斂次數(shù)和聚類(lèi)效果上具有一定的優(yōu)越性。在后續(xù)的工作中,將圍繞如何降低數(shù)據(jù)稀疏性對(duì)算法性能的影響等方面展開(kāi)。
參考文獻(xiàn)
[1] Zhao Xinchao. Simulated annealing algorithm with adaptive neighborhood[J]. Applied Soft Computing, 2011,11(2): 1827-1836.
[2] SZABO A, DE CASTRO L N, DELGADO M R. FaiNet: an immune algorithm for fuzzy clustering[C]. Fuzzy Systems (FUZZ-IEEE), IEEE, 2012: 1-9.
[3] 李鑫,張繼福,蔡江輝.一種基于大密度區(qū)域的模糊聚類(lèi)算法[J].小型微型計(jì)算機(jī)系統(tǒng),2012,33(6):1310-1315.
[4] Xie Xuanli, BENI G. A validity measure for fuzzy clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(8): 841-847.
[5] AMIG?魷 E, GONZALO J, ARTILES J, et al. A comparison of extrinsic clustering evaluation metrics based on formal constraints[J]. Information Retrieval, 2009, 12(4):461-486.

