摘 要: 子空間理論中被用于奇異值分解或特征值分解的自相關(guān)矩陣,通常可表示為接收向量與其自身轉(zhuǎn)置的乘積。提出了自相關(guān)矩陣的新型構(gòu)造算法。該算法構(gòu)造的自相關(guān)矩陣,特征值分解后其對噪聲不敏感,克服了常規(guī)子空間方法的弱點。仿真試驗表明,該方法應(yīng)用在高噪聲、低信噪比的實際通信環(huán)境下,特征值不會被噪聲湮沒,從根本上解決了傳統(tǒng)子空間分辨率不足的問題。同時,仿真表明,該方法對于多用戶擴頻信號同樣適用,可解決多用戶擴頻信號的碼元分離問題,其計算結(jié)果與理論計算一致,驗證了算法的正確性。
關(guān)鍵詞: 子空間理論;相關(guān)矩陣;特征值分解;直序列擴頻
0 引言
基于特征值分解(EVD)和基于奇異值分解(SVD)的子空間算法是近年來研究的熱門方向。其在信號處理方面,如信號的頻譜估計、陣列傳感器數(shù)據(jù)估計和其他參數(shù)估計[1]等方面越來越受到廣泛重視。但上述研究都是針對普通高信噪比情況下的調(diào)制信號而言,對于噪聲環(huán)境中的擴頻后的直擴信號罕有研究,對此,本文改進了子空間算法的分解矩陣——相關(guān)矩陣,對含噪情況下的直擴信號的分解算法做出了研究。
子空間[2]的相關(guān)矩陣(這里用R表示)可以用如下公式表示:
![]_XQP9)SK@_`SE}UIO0T)2I.png ]_XQP9)SK@_`SE}UIO0T)2I.png](http://files.chinaaet.com/images/2015/08/29/6357646658376200001385372.png)
其中yi代表第i個采樣窗口內(nèi)的采樣點數(shù)(共M個采樣點);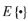 代表N個窗口內(nèi)所有數(shù)據(jù)的平均值。
代表N個窗口內(nèi)所有數(shù)據(jù)的平均值。
從上式可以看出,特征值的大小取決于信噪比而與統(tǒng)計窗口累計次數(shù)的多少并無關(guān)聯(lián)。由此可以得出結(jié)論,傳統(tǒng)子空間方法[3-4],僅僅依靠增加統(tǒng)計窗口個數(shù)是無法解決提取信號特征值[5],每個窗口如果都是處于較低信噪比的條件下,信號特征值仍然會湮沒在噪聲中。
區(qū)別于傳統(tǒng)子空間方法,本文提出的重構(gòu)方法,對R的建立不再采用missing image file的方式,而改用累乘的方法,即采樣后的一段數(shù)據(jù),各個窗口累乘,從而構(gòu)造出新的相關(guān)矩陣。下文簡稱該方法為累乘算法(Matrix Multiplication based Subspace,MMS)。
該算法構(gòu)造的新型矩陣具備如下特點:
(1)保留傳統(tǒng)子空間方法構(gòu)造矩陣的特性(在信號特征值與信噪比函數(shù)之間建立聯(lián)系)。
(2)分解后的信號特征值大小與累計窗口數(shù)量相關(guān)。即信號特征值既是信噪比(SNR)ρ的函數(shù)也是累積窗口分段數(shù)K的函數(shù)。
(3)分析窗口數(shù)量越多,信號特征值增長越快,而噪聲特征值幾乎不隨分析窗口的數(shù)量增長而增長。當累計窗口數(shù)量達到一定程度時,就能明顯區(qū)分出信號特征值與噪聲特征值。
文中最后將該算法構(gòu)造的相關(guān)矩陣用矩陣特征值分解后得到新的特性,并將直擴信號作為算法的輸入信號源,最終成功提取出多用戶直擴信號碼型。
1 直序列擴頻信號數(shù)學模型
直序列擴頻是將一個較窄的用戶信號,通過直接相乘,使其變成一種寬帶、高速率的碼元信號。由于信號速率提高,從頻域上看,其占用的帶寬相應(yīng)也變寬。
對本文使用到的各種數(shù)學符號作如下定義:
missing image file :用戶擴頻序列;
P:序列位數(shù)(長度);
Ts: 符號周期;
Te: 采樣周期;
Tc:碼片周期(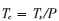 );
);
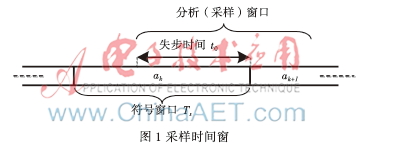
t0: 失步時間(采樣窗口與實際的符號起止窗口時間差),如圖1所示;
h(t):信號傳輸過程中所有信號畸變帶來的影響總和,也可以理解為傳輸鏈中發(fā)射端濾波器、信道濾波器、接收端濾波器和其他信道畸變影響帶來失真的卷積,表示如下:

missing image file:h(t)的矢量表示;
s(t): 擴頻信號經(jīng)接收機接收、解調(diào)后的基帶信號:

n(t):噪聲;
σ2: 噪聲方差;
y(t)=s(t)+n(t): 接收機解調(diào)輸出含噪信號。
對上述變量和以下要推導的公式,需做如下限定:
(1) 擴頻前用戶基帶信號ak在較長期限內(nèi)“+1”、“-1”數(shù)量大體相等,均值為零;
(2)n(t)為與信號ak相互獨立的(完全不相關(guān)的)高斯型白噪聲;
(3)通過參考文獻[6-7],已經(jīng)獲取到該擴頻信號的一些參數(shù),如射頻載波頻率f0、符號周期Ts、碼片周期Tc等。
對于假設(shè)(3),使用循環(huán)譜相關(guān)方法能夠在極低SNR下計算出碼片周期Tc和載波頻率f0。一旦f0可得,可以設(shè)計相應(yīng)下變頻接收機,通過NCO產(chǎn)生f0頻率,對射頻信號f0進行相乘,從而下變頻到基帶。
若Tc已知,為了后續(xù)計算的簡便,可將仿真采樣周期Te直接設(shè)置成Tc,但這樣僅僅為了計算方便,并非必要,即Tc可不知。
同樣,采用倒譜技術(shù)能估計出擴頻信號的符號周期Ts,將采樣窗口周期設(shè)置為Ts。
2 累乘算法
按照上節(jié)所述,每個采樣窗口時長為Ts,每個窗口內(nèi)再分為K段,K段內(nèi)又包含N個獨立計算窗口,每段單獨計算自相關(guān)。將K個自相關(guān)矩陣相乘,得到新算法后的帶分解矩陣:
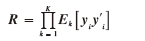
式中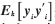 表示第k個N組窗口的均值;yi表示k段第i個窗口中采樣序列。yi為列矢量。
表示第k個N組窗口的均值;yi表示k段第i個窗口中采樣序列。yi為列矢量。
按照上述理論,采樣窗口周期設(shè)置為符號周期,單個采樣周期內(nèi)應(yīng)該橫跨兩個符號,其中一個符號為ak,保持時間為t0(t0為失步時間,未知);第二個符號表示為 ak+1,保持時間為整個符號周期減去上一個符號的保持周期(Ts-t0)。由于單個采樣周期內(nèi)存在兩個符號,對該采樣周期內(nèi)的相關(guān)矩陣分解后,將呈現(xiàn)兩個較大特征值,該特征值分別表示上述兩個符號,而其他特征值均為噪聲特征值:

![{P)%K7IX6I1K}22]7H$A2%G.png {P)%K7IX6I1K}22]7H$A2%G.png](http://files.chinaaet.com/images/2015/08/29/6357646702364600006359573.png)
根據(jù)式(3),有:
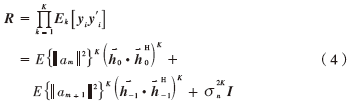
其中I為單位矩陣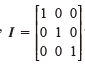 。由式(4)可以得出:矩陣
。由式(4)可以得出:矩陣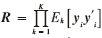 中存在兩個較大的特征值,每個值對應(yīng)特征矢量為missing image file/missing image file與系數(shù)的乘積。
中存在兩個較大的特征值,每個值對應(yīng)特征矢量為missing image file/missing image file與系數(shù)的乘積。
根據(jù)如下定義,可改寫式(4),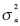 為基帶符號的方差,定義:
為基帶符號的方差,定義:
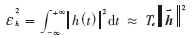
定義![5JUCE)KPOOVG}]917R{T46K.png 5JUCE)KPOOVG}]917R{T46K.png](http://files.chinaaet.com/images/2015/08/29/6357646789219500002607059.png) 如下:
如下:
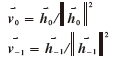
式(4)可改寫為式(5):
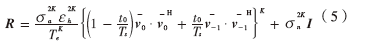
擴頻后的信號方差可表示為:
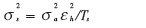
信噪比不直接采用信號比噪聲,也不采用dB為單位的對數(shù)表達式,定義如下:
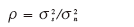
式(5)可改寫為:
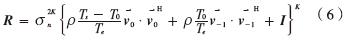
對矩陣(6)進行特征值分解,R的特征值中λ1、 λ2為上述表達符號矢量的兩個較大特征值(信號特征值),其他特征值λi(i≥3)則可稱為噪聲特征值,由系統(tǒng)中的各類噪聲引起。
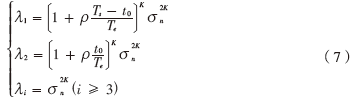
根據(jù)式(7),使用新型累乘構(gòu)造方法,λ1、λ2不僅與信噪比ρ有關(guān),同時也與分段數(shù)量K相關(guān)(即λ1、 λ2是ρ和K的函數(shù))。
比較傳統(tǒng)子空間相關(guān)函數(shù)構(gòu)造方法:
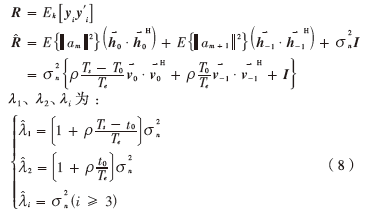
從式(8)可以得到,傳統(tǒng)方法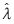 僅是信噪比ρ的函數(shù),而與參與計算的窗口數(shù)量沒有關(guān)系,窗口數(shù)量的提升不會改善信號特征值的分辨率。
僅是信噪比ρ的函數(shù),而與參與計算的窗口數(shù)量沒有關(guān)系,窗口數(shù)量的提升不會改善信號特征值的分辨率。
式(7)、式(8)之間關(guān)系為:

式(9)按級數(shù)序列展開公式簡化后得到:

為了進一步簡化,這里假設(shè):
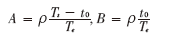
根據(jù)式(10),得到新算法特征值 λ1、λ2和λi之間的關(guān)系:
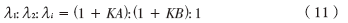
根據(jù)式(8),得到傳統(tǒng)算法特征值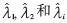 之間關(guān)系:
之間關(guān)系:
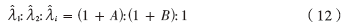
比較式(11)、式(12),低信噪比條件下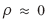 ,根據(jù)定義
,根據(jù)定義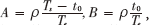 ,此時
,此時 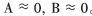 得出結(jié)論:使用傳統(tǒng)自相關(guān)算法構(gòu)造的矩陣,分解后得到的結(jié)果不能從噪聲特征值
得出結(jié)論:使用傳統(tǒng)自相關(guān)算法構(gòu)造的矩陣,分解后得到的結(jié)果不能從噪聲特征值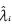 中有效地分辨出信號特征值
中有效地分辨出信號特征值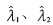 。而采用MMS累計得到的相關(guān)矩陣,分解后由于K為一個大的正整數(shù),能有效增加λ1、λ2與其他特征值λi之間的差異。
。而采用MMS累計得到的相關(guān)矩陣,分解后由于K為一個大的正整數(shù),能有效增加λ1、λ2與其他特征值λi之間的差異。
3 實驗結(jié)果
考慮到計算量的問題,在驗證該算法的有效性時,文中使用自相關(guān)、互相關(guān)性非常好的Gold碼作為擴頻序列,碼長設(shè)為63,調(diào)制類型設(shè)為QPSK (Quaternary Phase Shift Keying),信噪比設(shè)為SNR=-30 dB (按照如上定義,ρ=0.001),采用K×N=10 000個分析窗口,對算法進行驗證。
采樣周期Te=Tc=Ts/P,采樣窗口周期設(shè)為Ts,為了方便計算,信道內(nèi)沒有多徑干擾,失步系數(shù)設(shè)定為T0/Ts =0.4,失步時間t0原則上未知,但可通過式(10)得出。
按照上述參數(shù)設(shè)置,最終分解后的特征值:
missing image file

missing image file比例關(guān)系接近1:1:1,如圖2所示,信號特征值完全湮沒在噪聲特征值的波動之中。圖2與式(13)中的理論計算相吻合,此時不能獨立分離出信號特征值。
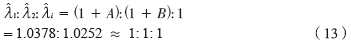

采用新算法MMS后,設(shè)定K=8, N=1 250,同樣10 000個窗口條件下的仿真結(jié)果,如圖3所示。表明missing image file之間比例關(guān)系:
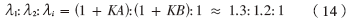
采用新算法后,可以明顯發(fā)現(xiàn)λ1、λ2受K的影響,能明顯分辨出信號特征值λ1、λ2與噪聲特征值λi之間的差異。
同樣,在不改變總窗口數(shù)量10 000的條件下,調(diào)整分段數(shù),使K=20, N=500,信號特征值與噪聲特征值比例關(guān)系理論上應(yīng)為:
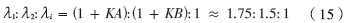
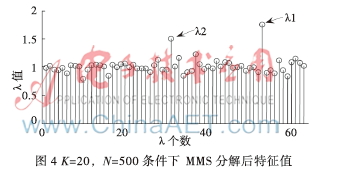
圖4證明了這一理論推導。同理,比較圖3、圖4,隨著K的增加,信號特征值λ1、λ2與噪聲特征值λi的差異越來越明顯。但總窗口數(shù)K×N一直為10 000,數(shù)量并未增加。K的增加導致每段內(nèi)窗口數(shù)N的減小;樣本數(shù)N的減小導致噪聲對待分解矩陣R的影響增大。每個分段求出的相關(guān)矩陣差異較大,所以累乘方法求出的信號特征值的均方差波動比傳統(tǒng)算法大。為了克服這一缺點,MMS算法適用于存在足夠多分析窗口(即樣本數(shù)足夠多)的情況下,此時N和K都能取得一個較大的數(shù)值,N的增大可減小每個相關(guān)矩陣的均方差波動,K的增大可提高信號特征值分辨率。
將信號特征值λ1、λ2代表的特征矢量組合,可得到待估計的Gold碼,組合方法不是本文討論重點,不再詳述,可參考文獻[8]。
4 結(jié)論
本文在近年來研究熱門子空間分解的基礎(chǔ)上,提出了一種對帶有噪聲信號的相關(guān)矩陣構(gòu)造方法。這一方法重新設(shè)計了信號相關(guān)矩陣的構(gòu)造算法,利用累乘計算,將各個分段矩陣互乘,計算量與傳統(tǒng)構(gòu)造方法相似。用擴頻信號驗證了該算法的理論推導與仿真,仿真結(jié)果表明,該算法實際計算與理論推導一致,可有效解決低信噪比條件下無法提取擴頻用戶碼序列的問題。同時,該算法也存在缺陷,即該算法需要樣本數(shù)量足夠多,并要保證N和K的取值都較大,這樣便可同時在低波動性和高分辨率兩項指標上都取得較好的結(jié)果。
參考文獻
[1] Van Der Veen A, DEPRETTERE E, SWINDLEHURST A. Subspace-based signal analysis using singular value decomposition [J]. Proceedings of IEEE, 1993,81(9): 1277-1308.
[2] Bensley S. E, AAZHANG B. Subspace-based channel estimation for code-division multiple-access communication systems [J]. IEEE Trans.Commun., 2011, 44: 1009-1020.
[3] GUSTAFSSON T, MACINNES C S .A class of subspace tracking algorithms based on approximation of the noise-subspace [J].Signal Processing Transactions on Acoustics, Speech, and Signal Processing IEEE 2010,48(11): 3231-3235.
[4] TUFTS D W, MELISSINOS C D. Simple effective computation of principle eignevectors and their eigenvalues and application to high resolution estimation of frequencies [J]. IEEE Trans. Acoust. Speech.Signal Processing, 2006, 34:1046-1053.
[5] PILLAI S U, BYUNG H K.GEESE (GEneralized Eigenvalues Utilizing Signal Subspace Eignevectors) - a new technique for direction finding [C]. Signals, Systems and Computers, 1988:568-572.
[6] BARUA S, HASHIMOTO T. Suboptimal MMSE multiuser receiver design for DS-CDMA multirate system using spectral correlations [C]. IEEE International Symposium on Information Theory, 2003: 446.
[7] OPPENHEIM A V, SCHAFER R W. From frequency to quefrency: a history of the cepstrum [J]. IEEE Signal Processing Magazine, 2014,21(5):95-106.
[8] NZOZA C N, GAUTIER R, BUREL G. Blind synchronization and sequences identification in CDMA transmissions [J]. IEEE MILCOM, 2004, 3:1384-1390.

