0 引言

　　隨著當(dāng)前通信系統(tǒng)集成度的不斷提高,，功放高效率、低功耗的要求顯得越來(lái)越重要,。傳統(tǒng)模擬功放為了保證放大信號(hào)的線性性能,，必須工作在線性區(qū)域，這大大限制了其效率性能,。而基于△∑調(diào)制器(DSM)的數(shù)字功放[1]通過(guò)將數(shù)字信號(hào)轉(zhuǎn)換為脈沖信號(hào),，驅(qū)動(dòng)晶體管工作在飽和開(kāi)關(guān)狀態(tài),，能夠大大提升功放的效率,。數(shù)字功放結(jié)構(gòu)圖如圖1所示。

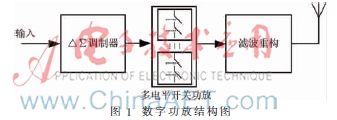
　　通過(guò)開(kāi)關(guān)工作,，數(shù)字功放理論上能夠獲得100%的效率,。但在實(shí)際電路中，當(dāng)前端DSM的輸出驅(qū)動(dòng)電平發(fā)生躍變時(shí),，開(kāi)關(guān)功放會(huì)消耗一定能量對(duì)電路中的電容進(jìn)行充放電,，從而影響數(shù)字功放的效率[2]。為了降低數(shù)字功放的切換損耗從而提升高頻場(chǎng)合下的功放效率,，需要盡量減少DSM輸出的切換頻率,。本文利用電力電子系統(tǒng)中的滯環(huán)比較控制思路，結(jié)合DSM結(jié)構(gòu)提出了一種新的量化策略,。該策略下DSM量化器通過(guò)記憶前一時(shí)刻的量化輸出,，實(shí)時(shí)更新當(dāng)前的量化門限值，從而在不改變DSM硬件結(jié)構(gòu)的前提下有效降低DSM輸出的切換速率,。

1 DSM量化策略

　　圖2所示為DSM的原理框圖[3],。

　　V(z)=Hu(z)U(z)+He(z)E(z)(1)

　　其中，Hu(z)為信號(hào)傳遞函數(shù),，He(z)為噪聲傳遞函數(shù),。根據(jù)DSM的結(jié)構(gòu),，減少DSM輸出切換頻率的一個(gè)直接方法是降低過(guò)采樣率。降低過(guò)采樣率時(shí),，為了保證帶內(nèi)SNR性能,，需要相應(yīng)地提高DSM階數(shù)。但無(wú)論是降低過(guò)采樣率還是提高DSM階數(shù),，都會(huì)改變DSM的環(huán)路濾波器結(jié)構(gòu),。為了在不改變DSM硬件結(jié)構(gòu)的前提下實(shí)現(xiàn)對(duì)輸出切換頻率的控制，考慮改進(jìn)量化器的量化策略?，F(xiàn)有的DSM結(jié)構(gòu)中,，量化器采用固定門限量化策略。對(duì)于單比特量化情況：

　　if(Y(n)>=0)

　　V(n)=1,；

　　else

　　V(n)=-1,；

　　end

　　1.1 單比特DSM的可變門限量化策略

　　在電力電子系統(tǒng)中，為了解決比較器輸入接近門限值時(shí)出現(xiàn)“振鈴”現(xiàn)象,，往往采用滯環(huán)比較器[4-5],，其基本特征是比較器采用不同的正、反向比較電壓,。借鑒滯環(huán)比較思路,，提出一種可變門限的DSM量化策略：

　　if(Y(n)>=-HV(n-1))

　　V(n)=1；

　　else

　　V(n)=-1,；

　　end

　　其中遲滯指數(shù)H>0,。在可變門限量化策略下，量化門限由固定值變?yōu)榕c前一時(shí)刻量化輸出相關(guān)的值,。假如前一時(shí)刻量化輸出為1(-1),，則當(dāng)前時(shí)刻量化器輸入值必須小于-H(大于H)其輸出才會(huì)發(fā)生改變。相比固定門限量化策略,，可變門限策略下量化器輸入需要變化更大的值才能最終引起輸出發(fā)生變化,。因此采用可變門限策略可以降低DSM輸出的切換頻率。

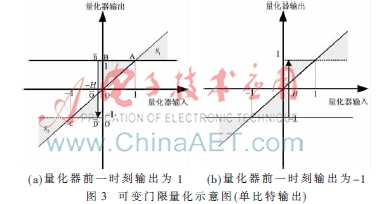
　　圖3為單比特量化示意圖,，陰影部分代表量化誤差,。固定門限量化策略下，量化器前一時(shí)刻輸出為1時(shí),，量化誤差面積為：

　　S=S1+S2+SOAB+SOCD(2)

　　可變門限量化策略下對(duì)應(yīng)的量化誤差面積為：

　　S′=S1+S2+SOAB+SOCD (3)

　　注意到對(duì)稱性,，相比固定門限，可變門限量化策略下量化誤差的總面積增加：

　　?駐S=S′-S=(SOAB-SOCD)-(SOAB+SOCD)=H2(4)

　　公式(4)表明,，相比固定門限量化,，可變門限量化策略下DSM輸出在切換頻率減小的同時(shí)SNR性能會(huì)有一定程度的下降。

　　1.2 多比特DSM的可變門限量化策略

　　進(jìn)一步根據(jù)公式(2)可以概括電平量化下可變門限策略的量化方案為：

　　假設(shè)固定門限量化策略下量化門限值為QL=[Q1,，Q2,，…,，Qn，…,，QN-1](-1<Qn<1,，1≤n≤N-1)。則在可變門限策略下,，若前一時(shí)刻的輸出為V(n-1)>Qn,，則當(dāng)前時(shí)刻下的量化門限變化為：Q=(Q1-H，Q2-H,，…,，Qn-H，…,，QN-1+H),。

　　容易驗(yàn)證，當(dāng)N=2時(shí),，上述的量化方案與式(2)一致,。

　　如圖4所示，對(duì)于固定門限量化策略,，2 bit DSM的量化門限為[-2/3,，0，2/3],。而在可變門限策略下,，根據(jù)前一時(shí)刻的量化輸出，多電平DSM門限值實(shí)時(shí)地進(jìn)行更新,。與單比特情況類似,，容易推出2 bit可變門限策略下量化誤差總面積增加量為3H2,。

2 仿真結(jié)果

　　前面通過(guò)理論定性分析了可變門限策略下DSM輸出序列的切換頻率及其SNR變化情況,，下面進(jìn)行仿真驗(yàn)證。不失一般性,，這邊考慮基于CRFB結(jié)構(gòu)的4階帶通DSM[6],，輸入為35 MHz單音信號(hào)，系統(tǒng)采樣頻率為400 MHz,。

　　2.1 遲滯指數(shù)范圍

　　為了保證DSM調(diào)制器的穩(wěn)定性,，首先分析不同輸入幅度下允許的最大遲滯指數(shù)。

　　圖5所示為DSM處于穩(wěn)定和失穩(wěn)時(shí)的輸出序列頻譜,。比較兩種情況,，可以看到失穩(wěn)時(shí)DSM序列頻譜的帶內(nèi)噪聲成型已經(jīng)不可見(jiàn)，并且?guī)獾男盘?hào)諧波和雜散幅度迅速增大,。因此以DSM輸出序列頻譜的帶內(nèi)SNR指標(biāo)作為穩(wěn)定性判據(jù),，以分析不同輸入幅度下允許的最大遲滯指數(shù),。

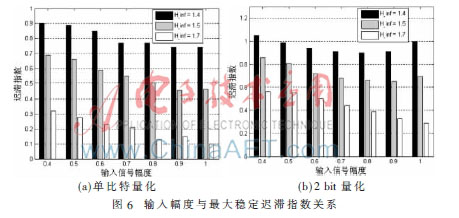
　　分析圖6仿真結(jié)果：在固定H_inf下，輸入單音信號(hào)幅度增加,，系統(tǒng)的穩(wěn)定性下降,，對(duì)應(yīng)此時(shí)量化器允許的最大遲滯指數(shù)整體上呈現(xiàn)下降趨勢(shì)；另一方面,，H_inf取值越小,，對(duì)應(yīng)DSM結(jié)構(gòu)越穩(wěn)定。因此相同輸入幅度下,，H_inf越小,，量化器允許的遲滯指數(shù)越大。與H_inf類似,，量化電平數(shù)越多DSM的穩(wěn)定性越好[3],。因此2 bit量化下的最大穩(wěn)定遲滯指數(shù)整體上要大于單比特量化。

　　2.2 平均切換頻率性能

　　下面在系統(tǒng)穩(wěn)定前提下仿真分析DSM輸出序列的切換頻率指標(biāo),。根據(jù)參考文獻(xiàn)[2],，定義平均切換頻率fav：

　　fav=1/Tav=Ntr×fs/N(5)

　　其中，fs為系統(tǒng)采樣頻率,；N為序列時(shí)鐘周期數(shù),；Ntr為高低電平間的切換次數(shù)，反映脈沖序列中的脈沖總數(shù),。仿真中遲滯指數(shù)取為[0,，0.2，0.4,，0.6],。

　　不同遲滯指數(shù)下的fav比較如圖7所示。遲滯指數(shù)越大,，則量化器輸入需要變化更大的值才能最終引起輸出發(fā)生變化,，對(duì)應(yīng)DSM輸出序列的fav越小。注意到2 bit量化情況下,，當(dāng)遲滯指數(shù)為0.6,、幅度為0.4時(shí)，此時(shí)DSM輸出序列的fav反而增大,。這是由于DSM實(shí)質(zhì)是一個(gè)負(fù)反饋系統(tǒng),，當(dāng)信號(hào)幅度較小且遲滯指數(shù)較大時(shí)，相比2 bit固定門限量化策略,，可變門限策略下量化器由于遲滯作用輸出電平在±1/3之外還將引入±1,，從而使得此時(shí)DSM輸出序列的fav增加。

　　2.3 帶內(nèi)信噪比性能

　　根據(jù)前面分析,，遲滯指數(shù)越大,，量化誤差也越大,。因此隨著遲滯指數(shù)增大，DSM輸出序列的帶內(nèi)SNR逐漸下降,，仿真結(jié)果如圖8所示,。

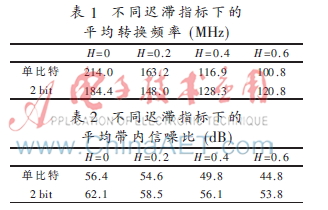
　　根據(jù)表1、2的定量分析結(jié)果,，相比固定門限策略,，當(dāng)H=0.2時(shí)，單比特和2 bit量化下fav分別減少23.7%和19.7%,，此時(shí)帶內(nèi)信噪比分別只下降了1.8 dB和3.6 dB,；當(dāng)H為0.6時(shí)，單比特和2 bit量化下帶內(nèi)信噪比分別下降了11.6 dB和8.3 dB,，此時(shí)fav分別減少52.9%和34.5%,。

3 結(jié)論

　　本文利用滯環(huán)比較控制思路，在DSM調(diào)制器中提出了一種可變門限的量化策略,，并通過(guò)理論和仿真分析了該策略下DSM輸出序列的平均切換速率fav以及帶內(nèi)SNR性能,。結(jié)果表明，相比固定門限量化策略,，可變門限量化策略通過(guò)設(shè)置合適的遲滯指數(shù),，在帶內(nèi)SNR性能下降有限的情況下能夠顯著的降低DSM輸出序列的平均切換頻率。因此,，基于本策略的DSM調(diào)制器可以有效減少高頻應(yīng)用場(chǎng)合下數(shù)字功放的切換損耗,，從而提升功放整體效率。另一方面,，考慮到本文策略下DSM輸出序列平均切換頻率降低是以犧牲一定的帶內(nèi)SNR性能為代價(jià),，考慮利用遺傳算法[7]、文化算法[8]等進(jìn)化策略優(yōu)化遲滯指數(shù)H,，從而在fav與SNR之間獲得一個(gè)最優(yōu)平衡是下步工作的方向,。

參考文獻(xiàn)

　　[1] 朱蕾，周強(qiáng),，譚笑.基于多比特帶通△∑調(diào)制器的射頻數(shù)字功放[J].電子技術(shù)應(yīng)用,，2013，39(8)：102-105.

　　[2] JOHNSON T,，STAPLETON S.RF Class-D amplification with bandpass sigma-delta modulator drive signals[J].IEEE Tran.on Circuits and System，2006,，53(12)：2507-2519.

　　[3] SCHREIER R,，TEMES G C.Delta sigma數(shù)據(jù)轉(zhuǎn)換器[M].北京：科學(xué)出版社，2007.

　　[4] 程瑜華,，鄺小飛,，孫玲玲.采用遲滯比較器的自激振蕩功率放大器行為特性分析[J].電路與系統(tǒng)學(xué)報(bào),，2012，17(6)：100-107.

　　[5] 彭彥豪,，張為,，劉洋.一種應(yīng)用于鎖相環(huán)頻率合成器的自動(dòng)選帶電路[J].微電子學(xué)，2011,，41(4)：498-501.

　　[6] 劉冠東.基于∑△技術(shù)的調(diào)制器的設(shè)計(jì)與驗(yàn)證[D].長(zhǎng)沙：湖南大學(xué),，2011.

　　[7] 周明，孫樹(shù)棟.遺傳算法原理及應(yīng)用[M].北京：國(guó)防工業(yè)出版社,，2002.

　　[8] 杜瓊,，周一屆.新的進(jìn)化算法——文化算法[J].計(jì)算機(jī)科學(xué)，2005,，32(9)：142-144.