文獻(xiàn)標(biāo)識碼: A
文章編號: 0258-7998(2014)12-0140-03
0 引言
隨著多媒體技術(shù)的發(fā)展及網(wǎng)絡(luò)的普及,人們欣賞音樂、獲取音樂資源變得十分便捷,而各種樂器也快速走進(jìn)音樂愛好者的家庭,如鋼琴、吉它等。
弦樂器因其物理特性,需要進(jìn)行定期校正[1-2],以往這項(xiàng)工作一直由經(jīng)過專業(yè)訓(xùn)練的調(diào)音師來承擔(dān)。即便是專業(yè)的調(diào)音師,也會受生理、心理以及客觀環(huán)境的影響,從而出現(xiàn)對音準(zhǔn)判斷的偏差;另外,隨著樂器快速普及,少量的專業(yè)調(diào)音師難以滿足廣大的需求,樂器校音成為難題[3]。因此,迫切需要一種儀器,可以完全排除調(diào)音過程中的主觀因素,能夠客觀準(zhǔn)確地校準(zhǔn)樂器。
1 基音檢測原理與常用算法
校音的根本目的就是精確確定樂音的基頻。信號基頻的檢測根據(jù)處理域或方法的不同,主要可分為時域方法和頻域方法。
1.1 時域方法
將信號看作時間的函數(shù),其波形反映依時間變化的特性,通過觀察信號波形,確定其基本周期,從而獲得基頻[4]。最常用的有自相關(guān)函數(shù)法。
自相關(guān)函數(shù)是信號自身的相關(guān)函數(shù),可以度量信號自身的相似性。對于無限長的離散信號x[n],自相關(guān)函數(shù)的定義為:

式中m為信號的延遲。
對于長度為N的離散信號x[n],自相關(guān)函數(shù)的定義為:
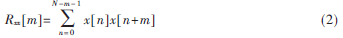
如果序列x[n]是周期的,則其自相關(guān)函數(shù)也是周期的,且周期相等。
1.2 頻域方法
頻域有更多的與基頻相關(guān)的信息。具有基頻的信號往往是由頻率具有諧波關(guān)系的信號組成,因此有很多利用頻域信息提取基頻的方法[5-6]。
諧波峰值法。諧波峰值法是基于離散傅里葉變換(DFT)的分析法,將信號通過FFT變換得到離散的頻譜,確定峰值頻率。對于周期信號而言,峰值頻率是基波頻率的整數(shù)倍,如果能確定峰值頻率對應(yīng)的諧波次數(shù),便可以求出基波頻率。
離散小波變換法。離散小波變換允許在連續(xù)的尺度上將信號分析為高頻成分和低頻成分,它是時間和頻率的局部變換,能有效地從信號中提取信息。
2 PFMCMR算法流程
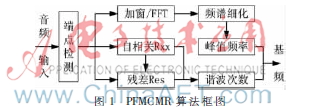
PFMCMR算法框圖如圖1所示。輸入音頻信號先進(jìn)行端點(diǎn)檢測[7-8],目的是去除噪聲和靜音段,以便僅對有用信號段進(jìn)行分析,有用信號段加窗后進(jìn)行傅里葉分析。設(shè)采樣頻率為Fs,窗長為N,則FFT的譜線間隔為f=Fs/N,一般這樣的精度離實(shí)際要求相差甚遠(yuǎn),因此需要通過頻率細(xì)化算法,以求得精度更高的峰值頻率。細(xì)化的頻率間隔可由具體算法的參數(shù)控制,根據(jù)實(shí)際需要精確到約千分之幾赫茲即可。
由前述可知,利用信號的自相關(guān)函數(shù)可以確定其基本周期,但由于實(shí)際信號的衰減、起伏及受噪聲影響等諸多因素,相關(guān)函數(shù)的峰值未必出現(xiàn)在基波周期處,更多時候出現(xiàn)在基波周期整數(shù)倍附近[9]。因此,直接將相關(guān)函數(shù)峰值的位置確定為基本周期既不可靠,精度也無法滿足實(shí)際需求。盡管如此,自相關(guān)函數(shù)為確定峰值頻率對應(yīng)的諧波次數(shù)提供了有用的信息。
自相關(guān)反映的是信號結(jié)構(gòu)的某種自相似程度,弦樂器音色豐富,音的結(jié)構(gòu)多變,所以,僅依據(jù)自相關(guān)函數(shù)來確定基波周期往往會導(dǎo)致倍頻或分頻。為了更準(zhǔn)確地確定峰值頻率對應(yīng)的諧波次數(shù),PFMCMR算法結(jié)合信號移位、相減后的殘差幅度值。自相關(guān)函數(shù)為計(jì)算殘差時的移位量提供了有用信息。
自相關(guān)函數(shù)的局部最大值和殘差幅度局部最小值相結(jié)合,可以有效地確定峰值頻率對應(yīng)的諧波次數(shù),從而最終計(jì)算出基頻。
3 PFMCMR算法的具體實(shí)現(xiàn)
為了方便定量敘述,取定一些參數(shù)如下:采樣頻率Fs=44 100 Hz,窗長N=4 096點(diǎn)。FFT譜線間隔為?駐f=Fs/N=44 100/4 096≈10.77 Hz。為了得到高精度的峰值頻率,可以采用頻率局部細(xì)化算法,如ZoomFFT或CZT[10],本文采用后者。PFMCMR算法的具體實(shí)現(xiàn)步驟如下:
(1)先計(jì)算FFT譜線幅度的最大值,其對應(yīng)的索引記為idxMaxFFT,從而可以確定峰值頻率一定在idxMaxFFT-1~idxMaxFFT+1對應(yīng)的頻率范圍內(nèi);
(2)取idxMaxFFT-1~idxMaxFFT+1頻率范圍進(jìn)行頻率細(xì)化,細(xì)化的倍數(shù)由CZT計(jì)算的頻率間隔數(shù)M決定,一般取M=N,因此,細(xì)化后的頻率間隔為?駐fM=2Fs/N2≈0.005 Hz;
(3)計(jì)算細(xì)化后的峰值頻率Fp,與之對應(yīng)的周期記為Tp;
(4)計(jì)算一幀信號的自相關(guān)函數(shù)Rxx[m],并求其峰值Rmax,對應(yīng)的索引m記為idxMaxR,根據(jù)實(shí)際情況,在搜索相關(guān)函數(shù)最大值時,需要排除Rxx[0]附近的數(shù)點(diǎn);
(5)計(jì)算Rxx[kTp],其中k為正整數(shù),且kTp≤idxMaxR,如果Rxx[kTp]/Rmax>THR,則kTp作為基波周期的候選值,記為kiTp,i為整數(shù),其最大值為基波周期的候選值的數(shù)目,其中THR為一閾值,本文取0.85;
(6)以kiTp為延遲點(diǎn)數(shù),計(jì)算殘差幅度的平均值:
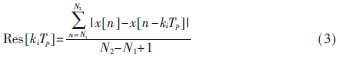
其中N1、N2為非負(fù)整數(shù)。
因?yàn)榉逯殿l率一定是基頻的整數(shù)倍,所以基波周期T0一定是kiTp中的某一個值,Rxx[kiTp]越大、Res[kiTp]越小,則kiTp為T0的可能性越大。所以引入?yún)?shù):
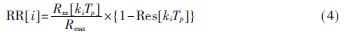
RR[i]越大,kiTp為T0的可能性越大,但由于實(shí)際信號的起伏多變,直接利用RR[i]作為參考值會造成一定概率的誤判,需要作一些置信修正,即RRM[i]=RR[i]·T[i],其中T[i]為置信因子,隨著i的增大而減小。最后求RRM[i]最大值,其對應(yīng)的i記為idxMaxRRM即為峰值頻率對應(yīng)的諧波次數(shù),所以,基頻F0=Fp/idxMaxRRM。
4 測試與性能分析
校音軟件兩個最重要的指標(biāo)是精確度和準(zhǔn)確度,為了測試精確度,采用單音正弦信號和定音器生成的標(biāo)準(zhǔn)音作為測試對象。用吉它和鋼琴音進(jìn)行整體性能測試。正弦單音由軟件生成,定音器的音、吉它音和鋼琴音采用現(xiàn)場錄制的方式。定音器A3、吉它G3、鋼琴B3音的時域波分別如圖2(a)、2(b)和2(c)所示。
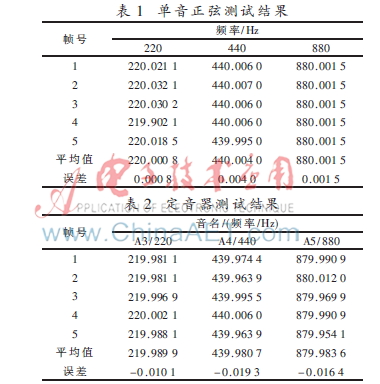
表1、表2分別為單音正弦和定音器的測試結(jié)果。可以看出,對于單音正弦信號,實(shí)測精度和理論分析相符合,誤差均在0.005 Hz以內(nèi)。相比而言,定音器的測試誤差要略大,這是因?yàn)橐纛l信號在采集過程中會發(fā)生失真。即便如此,精度仍在0.1 Hz以內(nèi)。
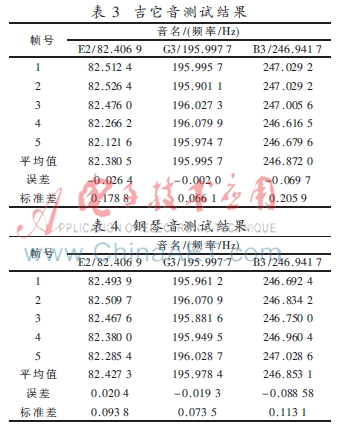
表3、表4分別為吉它和鋼琴3個音的測試結(jié)果。可以看出,每個音的誤差和標(biāo)準(zhǔn)差均未超過0.2 Hz。
綜合表1~表4的測試結(jié)果,表明PFMCMR算法具有高精度和良好的穩(wěn)定性,完全滿足實(shí)際應(yīng)用的要求。
5 結(jié)束語
本文針對弦樂器校音的基本問題,介紹了樂音基頻檢測的常用算法,并分析了這些算法的局限性。為了解決基頻檢測的精度和穩(wěn)定性問題,本文提出了一種基于弦樂器音頻信號時頻特性的校音新算法。利用頻譜細(xì)化方法得到高精度的諧波峰值頻率,時域中結(jié)合信號的相關(guān)函數(shù)和信號殘差,基于相關(guān)局部最大和殘差局部最小原則確定基波周期,從而計(jì)算出精確的基波頻率。測試結(jié)果表明,該方法精度高,穩(wěn)定性好,滿足實(shí)際應(yīng)用。
參考文獻(xiàn)
[1] FLETCHER N H,ROSSING T D.The physics of musical instruments[M].Springer,1998.
[2] SETHARES W A.Tuning,timbre,spectrum,scale[M].London:Springer,2005.
[3] 潘陽.鋼琴校音計(jì)算機(jī)軟件的設(shè)計(jì)[D].合肥:安徽大學(xué), 2011.
[4] AMADO R G.Pitch detection algorithms based on zero-crossrate and autocorrelation function for musical notes[C].Audio,Language and Image Processing,2008,ICALIP 2008,Inter-national Conference on,IEEE,2008:449-454.
[5] BENETOS E,DIXON S.Joint multi-pitch detection using harmonic envelope estimation for polyphonic music transcrip-tion[J].Selected Topics in Signal Processing,IEEE Journal of,2011,5(6):1111-1123.
[6] RIGAUD F,DAVID B,DAUDET L.A parametric model and estimation techniques for the inharmonicity and tuning of the piano[J].The Journal of the Acoustical Society of America,2013,133(5):3107-3118.
[7] KHOA P C.Noise robust voice activity detection[D].Singa-pore:Nanyang Technological University,2012.
[8] MA Y,NISHIHARA A.Efficient voice activity detection algorithm using long-term spectral flatness measure[J].EURASIP Journal on Audio,Speech,and Music Processing,2013,2013(1):1-18.
[9] BROWN J C,VAUGHN K V.Pitch center of stringed instrument vibrato tones[J].The Journal of the Acoustical Society of America,1996,100(3):1728-1735.
[10] MARTIN G.Chirp Z-transform spectral zoom optimization with MATLAB[Z].Sandia National Laboratories Report -7084,2005.

