文獻(xiàn)標(biāo)識(shí)碼: A
DOI:10.16157/j.issn.0258-7998.2015.10.027
中文引用格式: 史書(shū)明,姚穎莉,周杰. 三維空間域多徑信道模型的AOA和TOA特性分析[J].電子技術(shù)應(yīng)用,2015,41(10):100-102,106.
英文引用格式: Shi Shuming,Yao Yingli,Zhou Jie. Analysis of the AOA and TOA properties of the 3D spheroid model[J].Application of Electronic Technique,2015,41(10):100-102,106.
0 引言
近年來(lái),為滿(mǎn)足人們對(duì)無(wú)線(xiàn)通信不斷增長(zhǎng)的容量需求,通信系統(tǒng)的空時(shí)參量越來(lái)越受到人們廣泛關(guān)注。空間信道模型描述了多徑分量的到達(dá)角度和到達(dá)時(shí)延的相關(guān)數(shù)據(jù)信息,在設(shè)置天線(xiàn)陣列的無(wú)線(xiàn)通信系統(tǒng)的性能評(píng)估方面作用顯著。所有現(xiàn)存的幾何模型基本上都是二維的,如離散均勻模型[1-2]、橢圓散射模型[3]、圓形散射模型(CSM)[4]、高斯散射密度模型[5]、高斯AOA模型[6]等,上述模型均認(rèn)為信號(hào)傳輸發(fā)生在連接發(fā)射和接收天線(xiàn)頂端的一個(gè)平面上,僅推導(dǎo)和計(jì)算在水平面內(nèi)的空時(shí)信道參數(shù)。一些學(xué)者相繼提出了許多關(guān)于無(wú)線(xiàn)電信道的時(shí)間和空間特性的幾何模型,但大多在空間角度的研究上存在明顯的不足。針對(duì)宏小區(qū)環(huán)境下的移動(dòng)無(wú)線(xiàn)通信問(wèn)題,本文提出了一個(gè)三維空間域多徑信道幾何模型。重點(diǎn)研究模型的空時(shí)參量,給出電磁信號(hào)分別在移動(dòng)臺(tái)和基站的聯(lián)合、邊緣概率密度函數(shù)封閉式表達(dá)式以及傳輸路徑時(shí)延的封閉式表達(dá)式。此外還同時(shí)在方位角和仰角平面描述多徑波的到達(dá)角度和到達(dá)時(shí)延,允許在上述兩平面內(nèi)獨(dú)立控制其角度擴(kuò)展,并在此基礎(chǔ)上分析影響其時(shí)延特性的部分因素。
1 系統(tǒng)模型相關(guān)理論

本文提出的三維模型其主要散射體均勻地分布在MS附近,如圖1所示。圖中,a<D,b≤a,從BS到MS的直達(dá)路徑長(zhǎng)度可表示為dLOS。本文中的橢球體可被下式定義:

2 系統(tǒng)的三維空間特性AOA
2.1 電磁信號(hào)在MS端的到達(dá)角度
方位角的邊緣概率密度函數(shù)可通過(guò)對(duì)其聯(lián)合概率密度函數(shù)的變量依次積分獲得。同理可得仰角的邊緣概率密度函數(shù)。利用雅可比變換可得MS處聯(lián)合概率密度,對(duì)其rm進(jìn)行積分,可得:

對(duì)上式的?茁m進(jìn)行積分并通過(guò)t=sin m變量代換得方位角在(0,2π)內(nèi)均勻分布,且與BS天線(xiàn)的高度無(wú)關(guān)。對(duì)式(2)中的m進(jìn)行積分即可獲得關(guān)于仰角的概率密度函數(shù):
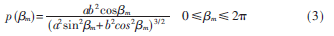
從上式可以看出,仰角m的概率密度函數(shù)的圖形形狀僅與橢球體b/a的比率有關(guān)。從式(2)和式(3)可見(jiàn),MS的仰角與方位角是統(tǒng)計(jì)獨(dú)立的。
2.2 電磁信號(hào)在BS端的到達(dá)角度
利用雅可比轉(zhuǎn)換式,可得BS處的聯(lián)合概率密度函數(shù)。對(duì)其rb的所有可能取值進(jìn)行積分,可得其關(guān)于角度的邊緣概率密度函數(shù):

其中,rb1和rb2是從BS端角度為(b,βb)處引的一條直線(xiàn)與半橢球體的交點(diǎn)。
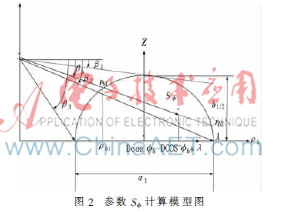
圖2示出了半橢球體與b確定的平面的交點(diǎn)構(gòu)成的半橢圓S的幾何形狀。橢圓的中心、徑向長(zhǎng)度均如圖所注。sin?準(zhǔn)max=a/D,與BS的天線(xiàn)高度無(wú)關(guān)。綜上,概率密度函數(shù)p(b)表達(dá)式為:
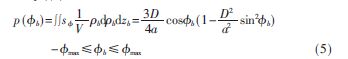
從上式可見(jiàn)BS處方位角概率密度函數(shù)與軸長(zhǎng)b無(wú)關(guān)。
3 系統(tǒng)的時(shí)延特性TOA
傳輸時(shí)延,計(jì)算可得rm為:

其中rm在式(6)中已給出,利用雅可比變換并帶入式(7)中即可得到TOA/AOA的聯(lián)合概率密度函數(shù),其公式如下:

相似地,在BS的對(duì)應(yīng)角的聯(lián)合概率密度函數(shù)也可得到,其中V=2πa2b/3。利用積分依次可得BS端到達(dá)時(shí)延的相應(yīng)聯(lián)合概率密度函數(shù)式如下:

同理可得MS端的方位角、仰角到達(dá)時(shí)延聯(lián)合概率密度函數(shù)。對(duì)上述兩式中任一公式的相應(yīng)角進(jìn)行積分即可獲得到達(dá)時(shí)延邊緣概率密度函數(shù),即:

4 數(shù)值結(jié)果與分析
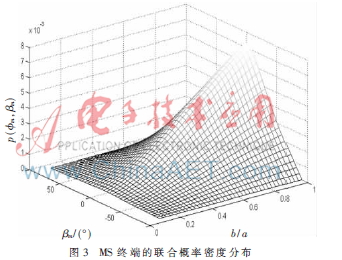
仿真實(shí)驗(yàn)的結(jié)果將在此部分進(jìn)行分析。圖3描述的為不同b/a取值情況下仰角?茁m對(duì)應(yīng)的概率密度函數(shù)的三維圖,從圖中可以發(fā)現(xiàn),當(dāng)b/a較大時(shí),在豎直平面上的切平面較大,從而多徑信號(hào)AOA的概率密度相對(duì)較大。從圖中還可發(fā)現(xiàn)移動(dòng)臺(tái)BS端的發(fā)射信號(hào)基本在小角度(m為零度)或者b/a參數(shù)值較大處,而在大角度(m為直角)時(shí)其概率密度較小,幾乎為零。所有曲線(xiàn)中最常發(fā)生的角在m=0處,此時(shí)3D模型轉(zhuǎn)化為2D模型,無(wú)論b/a數(shù)值如何變化,其切平面都相同,故俯仰平面AOA概率密度值相等為零。研究比較發(fā)現(xiàn):本文提出的模型,其基站處方位角的概率密度函數(shù)(見(jiàn)式(5))不同于散射半徑為a的二維CSM模型的PCSM(b)。
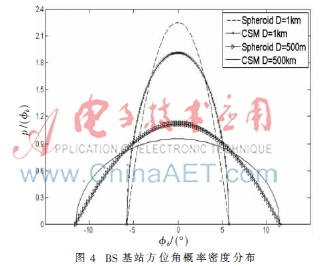
圖4描述的是本文提出的半橢球模型和CSM模型在方位角平面對(duì)應(yīng)不同D值的概率密度樣值函數(shù)分布情況。正是由于深度和高度的綜合作用,與CSM相比,本文提出的橢球模型的離軸散射體才會(huì)與其不同。
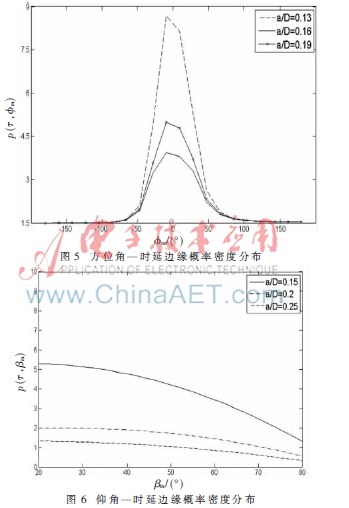
圖5、圖6分別描述了關(guān)于方位角以及仰角的TOA聯(lián)合概率密度函數(shù)的幾何分布情況。從圖5可以發(fā)現(xiàn),由于空間分布關(guān)于豎直平面對(duì)稱(chēng)(見(jiàn)圖1),使得TOA聯(lián)合概率分布波形被挖掉時(shí)延不存在的兩片區(qū)域,左右處于對(duì)稱(chēng)狀態(tài),故其圖形結(jié)果在-Φm~Φm之間對(duì)稱(chēng)分布。移動(dòng)臺(tái)接收信號(hào)基本在小角度(Φm=0)處,而在角度增大至180°時(shí)其概率密度分布相當(dāng)小,且其關(guān)于方位角的TOA概率函數(shù)值在Φm=0處到達(dá)峰值。由圖6的波形分布可知, a/D不斷增加,關(guān)于仰角的TOA聯(lián)合概率密度函數(shù)值不斷衰弱,當(dāng)傳輸時(shí)延超過(guò)最大傳輸時(shí)延即超過(guò)散射區(qū)域,其概率密度為零;當(dāng)俯仰平面的角度βm不斷增大時(shí),遠(yuǎn)離MS端的散射體逐漸增多,電磁信號(hào)的反射和折射概率相對(duì)較大,故導(dǎo)致關(guān)于仰角的TOA概率密度不斷減小[9]。如果令式(8)中的βm和Ht值均為零,則可由本模型推導(dǎo)出文獻(xiàn)3中提出的一個(gè)二維模型。
5 結(jié)語(yǔ)
針對(duì)室外宏蜂窩環(huán)境等因素造成的多徑信道衰落,本文提出的3D模型的幾何參數(shù)有:橢球體的軸長(zhǎng)a、b,基站天線(xiàn)的高度Ht,負(fù)責(zé)發(fā)送的基站與負(fù)責(zé)接收的移動(dòng)臺(tái)之間的水平距離D。揭示了此模型下BS和MS端在水平面和俯仰面上各信道參數(shù)的變化特征。在移動(dòng)臺(tái)處,方位角的多徑波均勻分布,仰角的多徑波分布僅與a和b有關(guān)。在基站處,方位角的概率密度函數(shù)與單一變量a/D密切相關(guān),而仰角的概率密度函數(shù)不僅與a/D有關(guān),還與b/D和Ht/D有關(guān)。對(duì)于時(shí)延特性,其概率密度函數(shù)也與a/D有密切關(guān)系。當(dāng)存在的散射體與發(fā)射機(jī)和接收機(jī)部分的距離不斷增加,傳播時(shí)延會(huì)相應(yīng)的延長(zhǎng)。本文提出的模型在宏蜂窩環(huán)境中非常有用,基于本文對(duì)散射區(qū)域水平與垂直方向的角度擴(kuò)展,使用平面天線(xiàn)陣列對(duì)無(wú)線(xiàn)電通信系統(tǒng)進(jìn)行性能分析的精度會(huì)越來(lái)越高。而這些性能分析又能夠在進(jìn)一步提高通信系統(tǒng)流數(shù)據(jù)速率方面加以使用。
參考文獻(xiàn)
[1] LEE W C.Mobile communications engineering[M].New York:McGraw-Hill Professional,1982.
[2] SUZUKI H.A statistical model for urban radio propagation[J].Communications,IEEE Transactions on,1977,25(7):673-680.
[3] ERTEL R B,REED J H.Angle and time of arrival statisticsfor circular and elliptical scattering models[J].Selected Areasin Communications,IEEE Journal on,1999,17(11):1829-1840.
[4] PETRUS P,REED J H,RAPPAPORT T S.Geometrically based environments[C].Global Telecommunications Conference,1996.GLOBECOM′96.′Communications:The Key to Global Prosperity.IEEE,1996(2):1197-1201.
[5] JANASWAMY R.Angle and time of arrival statistics for theGaussian scatter density model[J].Wireless Communications,IEEE Transactions on,2002,1(3):488-497.
[6] NAWAZ S J,KHAN N M,PATWARY M N,et al.Effect ofdirectional antenna on the Doppler spectrum in 3-D mobileradio propagation environment[J].Vehicular Technology,,IEEE Transactions on,2011,60(7):2895-2903.
[7] ZHOU J,CAO Z G,HISAKAZU K.Asymmetric geometrical-based statistical channel model and its multiple-input and multiple-output capacity[J].IET Communications,2014,8(1):1-10.

