文獻標(biāo)識碼： A
DOI：10.16157/j.issn.0258-7998.2015.11.037
中文引用格式： 李雅,，陳友興，任陽山,，等. 基于k-wave超聲場時域仿真研究[J].電子技術(shù)應(yīng)用,，2015，41(11)：132-134,，139.
英文引用格式： Li Ya,，Chen Youxing，Ren Yangshan,，et al. Based on the k-wave ulrasonic field in time domain simulation[J].Application of Electronic Technique,，2015，41(11)：132-134,，139.
0 引言
在無損探傷過程中,，探頭處發(fā)射的超聲波在缺陷中經(jīng)過發(fā)射被超聲波探傷儀接收，以確定缺陷的位置和類型,。無損探傷具有檢測成本低,、速度快和現(xiàn)場使用方便等優(yōu)點，多用于管道,、壓力容器等圓柱體構(gòu)件的探傷檢測[1],。計算超聲學(xué)在近些年應(yīng)用于超聲波檢測的模擬，從不同尺度上入手,，建立不同的超聲波模型,，來模擬聲束在介質(zhì)中傳播時的聲場、缺陷與界面處對超聲波的作用規(guī)律,，構(gòu)建超聲波檢測計算模型,，整合發(fā)展超聲波檢測的技術(shù)，促進超聲波檢測在無損檢測中的應(yīng)用,。對于許多復(fù)雜情況而言,，理論與實驗手段難以進行，但可以利用計算機環(huán)境進行仿真計算得到數(shù)值結(jié)果[2],。本文利用MATLAB加載的k-wave工具箱模擬聲場傳播和建立缺陷重構(gòu)模型,，使得原有聲場建模變得簡單、快速[3],。
1 超聲場仿真原理
本文在均勻背景散射媒介中建立聲源模型,，簡化輸入?yún)?shù)在提高計算效率的同時，排除非關(guān)鍵因素,，從而有效提取出超聲場的精確回波模型,。
1.1 聲速與聲壓的計算
由流體介質(zhì)中的非線性壓力與密度關(guān)系，可以將狀態(tài)擴展為泰勒級數(shù)中對應(yīng)的壓力項和密度項,。假設(shè)非線性和壓力的變化影響(由于聲波吸收)都是二階,。因此，高階壓力項可以被丟棄,?？紤]到在很小的有限時間步長t=t1-t0內(nèi)改變流體元素的總壓強，泰勒級數(shù)展開可寫成：
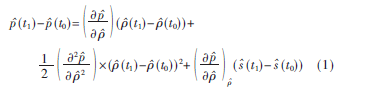
式(1)中最后一部分代表一種能量損失也是一種聲能吸收,。在熱粘性介質(zhì)中,，可以結(jié)合介質(zhì)的導(dǎo)熱系數(shù)和比熱容，考慮能量守恒方程[4],，這一點可以表示為一種聲學(xué)損失模型：
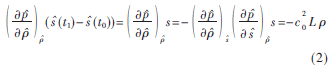
L表示聲能損失,。建立冪律吸收模型，基于分數(shù)拉普拉斯算子定義L的表達式為[5]：
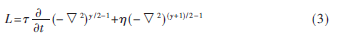
τ和η是吸收和色散比例系數(shù)[6],。
1.2 k-space偽譜法
偽譜法求解微分方程主要包含：(1)離散化處理,，用一定的方式在整個區(qū)域上選取格點構(gòu)成一個網(wǎng)絡(luò)。而其它點上的變量值可以用插值的方法得到,；(2)選取合適的基函數(shù)變量值的情況下構(gòu)造插值函數(shù),，計算格點上變量值的空間導(dǎo)數(shù),。偽譜法是全局方法,只能用在空間域。如果所求解的是含時微分方程,，一般用簡單的有限差分方法來處理時間域的計算[7],。
在k-wave中，利用快速傅里葉變換和k-space偽譜法,，將守恒方程中的粒子速度和聲學(xué)密度轉(zhuǎn)換為離散形式,，計算每個時間步長內(nèi)聲壓場的變化情況，能夠高效準確地對超聲場進行數(shù)值模擬,。離散表達式如式(4)～式(7)所示：
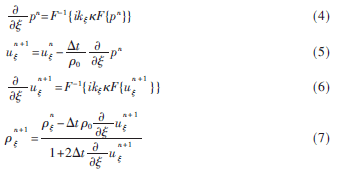
聲學(xué)密度是分布在笛卡兒坐標(biāo)系中并可以引入各向異性PML應(yīng)用的值[8],。F和F-1表示空間傅里葉正逆變換，上標(biāo)n和n+1分別表示函數(shù)在當(dāng)前和下一時間點的值,，i為虛數(shù)單位,，t是時間步長，其中cref為相關(guān)聲速,。
式(7)離散方程可利用基于Courant-Friedrichs-Lewy的CFL數(shù)值求解時間步長,，?駐t=CFL?駐x/cmax。CFL通常取0.3能夠平衡準確性和計算效率之間的關(guān)系,。在每個時間步長內(nèi),，質(zhì)量或力源可以通過在計算域內(nèi)添加適當(dāng)?shù)木W(wǎng)格點值來設(shè)置。同樣的,，模擬的輸出可以通過每個時間步長在特定的網(wǎng)格點處的聲變量記錄[9-10],。
2 聲場仿真模型
本文設(shè)計圓柱體工件超聲場模型，并通過傳感器接受回波信號,。工件的設(shè)定如下：實心圓工件半徑為2 mm,；人造缺陷孔工件中心圓孔工件外半徑為2 mm，內(nèi)半徑為1 mm,；偏心圓孔工件外半徑2 mm,，偏心孔中心為半徑的中間，半徑為0.5 mm,，在距離圓柱的中心半徑為4.5 mm處設(shè)置8個等距離分布的傳感器,。時間步長為1 μs，由于超聲波傳播速度很快且工件尺寸很小,，本文對超聲波在工件內(nèi)和水中聲速的差異不做考慮,，超聲波傳播速度為1 500 m/s。
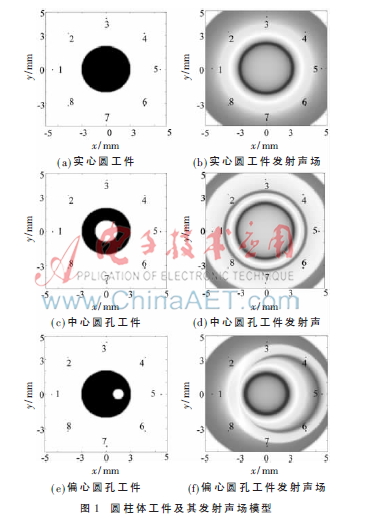
根據(jù)惠更斯原理,，聲波遇到障礙物時會以障礙物作為新的聲源發(fā)射,。本文仿真環(huán)境以圓柱體工件為新的聲源，并設(shè)定了8個點傳感器的分布位置及其編號，工件將360°接收的單脈沖信號在同一時刻發(fā)射出去,，如圖1所示為不同構(gòu)件發(fā)射聲場模型的二維顯示圖,，從中可以很直觀地觀測到聲場傳播過程中波形和聲壓強弱情況，深色到淺色區(qū)域即為聲壓從強到弱體現(xiàn),。
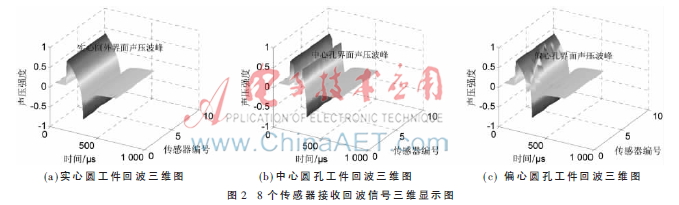
圖2為8個點傳感器探頭接收的超聲信號三維圖,，通過與實心圓對比可以明顯看出中心圓孔和偏心圓孔發(fā)射聲場聲壓的異同之處：(1)由于圓柱位置及外半徑設(shè)置相同,，傳感器探頭接收信號的起始和終止位置一樣,；(2)由于中心圓孔的設(shè)定位置在傳感器探頭的正中心，所以8個探頭接收到的信號同一時刻達到波峰,；(3)根據(jù)偏心圓孔設(shè)定的位置,， 5號最近點傳感器會首先接收到回波信號，1號最遠點傳感器則會最后接收到超聲的二次回波信號,。
3 逆時反演重構(gòu)模型
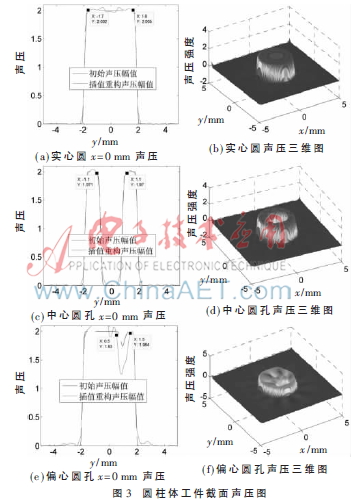
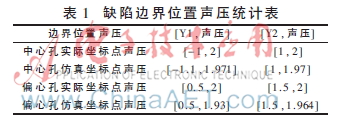
利用聲學(xué)傳感器接收到的回波信號逆時反演重構(gòu),，在圓周上每隔一度設(shè)置一個點傳感器，使之圍繞工件一周,，充分接收到不同工件360°的發(fā)射聲場,，利用接收到的發(fā)射信號進行逆時反演重構(gòu)，仿真重構(gòu)效果如圖3(b),、圖3(d)～圖3(f)所示,。如圖3(c)，圖3(e)所示,，聲壓在人造缺陷孔的邊界位置將會有明顯變動,，缺陷邊界處聲壓坐標(biāo)值如表1所示。根據(jù)測量數(shù)據(jù)可知,，在誤差允許范圍內(nèi)缺陷仿真邊界坐標(biāo)點位置與實際缺陷設(shè)定尺寸相一致,。
4 總結(jié)
本文利用k-wave工具箱對三種典型的工件模型做了聲場仿真研究，設(shè)計的仿真平臺能夠達到實際檢測中難以實現(xiàn)的設(shè)定,，能夠?qū)崿F(xiàn)360°同時刻采集工件的發(fā)射信號,，減少人為移動工件或探頭進行超聲探測掃描帶來的誤差等方面的影響因素，并且能夠?qū)⒙晥瞿芰烤唧w化,，直觀可視化地觀測聲場在工件中具體傳播過程,。通過重構(gòu)結(jié)果分析，測得缺陷的位置和尺寸數(shù)據(jù)與工件的實際設(shè)定值相一致,，充分說明仿真理論的正確性和仿真結(jié)果的準確性,。
參考文獻
[1] 孟凡凱.水下超聲波檢測聲場數(shù)值模擬與實驗分析[D].哈爾濱：哈爾濱工業(yè)大學(xué)，2012.
[2] COX B T,，TREEBY B E.Effect of Sensor Directionality on Photoacoustic Imaging:A Study Using the k-Wave Toolbox.Proc.of SPIE Vol.2010,，7564，75640I1-75640I6.
[3] TREEBY B E，COX B T.K-Wave：a MATLAB toolbox for simulation and reconstruction of photoacoustic wave-fields[J].J.Biomed.Opt.,，2010,，15(2)，0213141-02131412.
[4] COX B T,，KARA S,，ARRIDGE S R，et al.K-space prop-agation models for acoustically heterogeneous media：Appli-cation to biomedical photoacoustics[J].J.Acoust.Soc.Am.2007,，121(40)：3453-3464.
[5] 《超聲波探傷》編寫組.超聲波探傷[M].北京：電力工業(yè)出版社,，1980.
[6] Tabei M，Mast T D,，Waag R C.A k-space method for coupled first-order acoustic propagation equations[J].Acoust.Soc.Am,，2002，111(1)：53-63.
[7] 劉魯波,，陳曉非,，王彥賓.切比雪夫偽譜法模擬地震波場[J].西北地震學(xué)報，2007（01）：18-25.
[8] COX B T,，KARA S,，ARRIDGE S R，et al.K-space prop-agation models for acoustically heterogeneous media：Appli-cation to biomedical photoacoustics[J].Acoust.Soc.Am,，2007,，121(6)：3453-3464.
[9] Tillett J C，Daoud M I,，Lacefield J C,，et al.A k-space method for acoustic propagation using coupled first-order equations in three dimensions[J].Acoust.Soc.Am，2009,，126(3)：1231-1244.
[10] TREEBY B E,，JAROS J，RENDELL A P.Modeling nonlinearultrasound propagation inheterogeneo us media with power law absorption using a k-space pseudospectral method[J].Acoust.Soc.Am,，2012,，131(6)：4324-4336.