摘 要: 提出了一種新型的混合算法并命名為混合雜草蝙蝠算法(Hybridize Invasive Weed Optimization with Bat Algorithm,,IWOBA),,該算法在雜草算法的基礎(chǔ)上利用蝙蝠算法的回聲定位來解決每代種子逐步尋優(yōu)的問題。其原理是利用種群速度和位置的不斷更新,,增加種群的多樣性,,從而達(dá)到提高種群的全局收斂性。最后利用6個(gè)測試函數(shù)對該算法和標(biāo)準(zhǔn)雜草算法進(jìn)行測試比較,。仿真結(jié)果表明,,IWOBA能夠有效克服原算法早熟、易陷入局部最優(yōu)的缺點(diǎn),,可加快算法收斂速度,,具有良好的魯棒性。
關(guān)鍵詞: 雜草算法,;蝙蝠算法,;回聲定位
0 引言
入侵雜草算法(Invasive Weed Optimization,,IWO)是由德黑蘭大學(xué)的Mehrabian等在2006年提出來的,它是一種模擬自然界雜草入侵的新型的數(shù)值優(yōu)化算法,。該算法具有很強(qiáng)的魯棒性和適應(yīng)性,,并且具有易于理解及實(shí)現(xiàn)等特點(diǎn)。近幾年來,,在很多學(xué)者的研究下,,雜草算法已經(jīng)成功應(yīng)用到圖像聚類、工程約束設(shè)計(jì)以及DNA編碼等眾多領(lǐng)域中[1-2],。
與其他智能算法相比較,,標(biāo)準(zhǔn)雜草算法本身存在易于陷入局部最優(yōu)解和收斂精度不高的不足,這些不足都影響著算法的尋優(yōu)效果,。因此,,Hajimirsadeghi和Lucas提出了一種IWO和PSO融合的算法[3],利用位置和速度的更新,,使得算法避免了局部最優(yōu)解,;Zhang Xuncai等人在標(biāo)準(zhǔn)IWO算法中引入了交叉算子,避免算法早熟,,提高了全局最優(yōu)解[4],;張玉等人將遺傳算法中的選擇機(jī)制加入到標(biāo)準(zhǔn)IWO算法中,從而提高算法的多樣性[5],。
而本文是將蝙蝠算法中的回聲定位原理應(yīng)用到雜草算法中,。通過回聲定位的特性,對種子個(gè)體的位置和速度進(jìn)行不斷地更新,,使其避免出現(xiàn)早熟和陷入局部最優(yōu)解的情況,。且改進(jìn)后的算法有更高的收斂精度。為了驗(yàn)證改進(jìn)后算法的有效性,,本文通過6個(gè)常用的標(biāo)準(zhǔn)測試函數(shù)進(jìn)行仿真實(shí)驗(yàn),。
1 算法介紹
1.1 標(biāo)準(zhǔn)雜草優(yōu)化算法
在雜草優(yōu)化中,雜草通過繁殖產(chǎn)生種子,,種子經(jīng)過空間的擴(kuò)散,、生長和競爭排除,從而得到適應(yīng)度較高的個(gè)體,。其過程如下[6]:
?。?)初始化種群和參數(shù):在D維數(shù)下產(chǎn)生N個(gè)可行解。
?。?)種群的生長繁殖:適應(yīng)度高的雜草會產(chǎn)生更多的子代,,適應(yīng)度小的會慢慢消失。其計(jì)算公式:
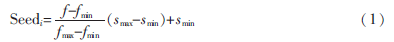
式中,f是當(dāng)前種群適應(yīng)度,;fmax和fmin分別是種群的最大和最小適應(yīng)度,;smax和smin分別表示種群的最大規(guī)模和最小規(guī)模。
?。?)空間擴(kuò)散:種群所產(chǎn)生的種子按平均值為0,、標(biāo)準(zhǔn)差為δ的正態(tài)分布方式和步長Step∈[-δ,δ]分布在D維空間,。在迭代初期標(biāo)準(zhǔn)差δ較大,,隨著δ逐漸減小,迭代步長也在逐漸減小,。其公式如下:
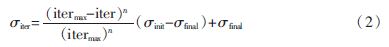
?。?)競爭排除:種群經(jīng)過多次繁殖之后,,其種群規(guī)模達(dá)到最大數(shù)量Pmax時(shí),,將種群中的個(gè)體根據(jù)適應(yīng)度的大小進(jìn)行排列,保留適應(yīng)度前Pmax個(gè)個(gè)體,。適應(yīng)度差的個(gè)體將被淘汰,。
1.2 蝙蝠算法
蝙蝠算法是受蝙蝠利用回聲定位來撲捉獵物和蔽障的啟發(fā)所提出的啟元式算法[7]。其原理是蝙蝠通過調(diào)整頻率的大小來不斷更新其位置和速度從而達(dá)到撲捉獵物的目的,。其速度和位置更新公式為:

式中,,?茁∈[0,1]是一個(gè)隨機(jī)變量,,x*是當(dāng)前最佳位置,。在波長不變的情況下,fmin=0,,fmax=100,;開始每只蝙蝠的頻率都是隨機(jī)分配的。在進(jìn)行局部搜索時(shí),,每只蝙蝠的最新解都是從現(xiàn)有的解集中選擇的:
Xnew=Xold+εAt(6)
其中,,ε∈[-1,1]是一個(gè)隨機(jī)數(shù),,A是平均響度,;隨著迭代的進(jìn)行,蝙蝠在捕捉時(shí)脈沖所發(fā)的速率和響度也在不斷更新,。更新公式為:

其中,,?琢和?酌一般都為0.9,隨著迭代的進(jìn)行,,脈沖響度 A趨向于0,,脈沖速率r趨向于r;通過脈沖頻率速度和響度的不斷更新,使每個(gè)蝙蝠飛向最優(yōu)解,。
1.3 雜草算法與蝙蝠算法的融合算法BAIWO
利用回聲定位的方法來更新雜草種群中個(gè)體的位置和速度[8],,具體實(shí)施步驟如下:
(1)初始化BAIWO的參數(shù),,并隨機(jī)產(chǎn)生N0個(gè)個(gè)體的種群,;
(2)計(jì)算種群個(gè)體的適應(yīng)度函數(shù)值,,確定當(dāng)前最優(yōu)值和最優(yōu)解,;
(3)種群個(gè)體進(jìn)行繁殖,、生長:
?、賹ΨN群中每個(gè)種子利用式(3)~式(5)進(jìn)行位置和速度更新;
?、诟鶕?jù)當(dāng)前解集隨機(jī)產(chǎn)生一個(gè)新解,,并對該新解進(jìn)行約束;
?、弁ㄟ^條件(rand<Ai & f(xi)<f(xi))來判斷是否接受該新解,,以及是否更新ri和Ai;
?。?)判斷種群是否達(dá)到最大規(guī)模,,若未達(dá)到,轉(zhuǎn)到步驟(3),,若達(dá)到,,則繼續(xù)執(zhí)行;
?。?)對種群個(gè)體的適應(yīng)度值進(jìn)行排序,,保留前最大規(guī)模數(shù)的個(gè)體;
?。?)判斷是否達(dá)到最大迭代數(shù),,若否,轉(zhuǎn)到步驟(3),,若是,,輸出最優(yōu)值和最優(yōu)解。
從上述BAIWO算法的描述過程可知,,BAIWO算法中的個(gè)體并不是在每次迭代過后直接進(jìn)入下一代繁殖,、生長,而是在種群中個(gè)體進(jìn)行位置和速度更新后找出更優(yōu)的個(gè)體進(jìn)行下一代繁殖,。這樣,,在迭代初期可以使得種群有著更強(qiáng)的全局搜索能力,到達(dá)迭代后期時(shí),種群的尋優(yōu)步長在不斷變小,,使得其具有更強(qiáng)的局部搜索能力,。所以,BAIWO算法是將BA算法和IWO算法的各自優(yōu)點(diǎn)融合起來,,使得改進(jìn)后的算法在初期擁有很好的全局搜索能力,,到達(dá)后期對局部搜索更精確。從而克服了IWO算法前期陷入局部搜索,,以及后期收斂精度不高和速度慢等缺陷[9-10],。
1.4 BAIWO算法時(shí)間復(fù)雜度分析
根據(jù)上述的BAIWO算法的流程步驟來對該算法進(jìn)行時(shí)間復(fù)雜度分析,設(shè)n為種群個(gè)體的數(shù)目,,d為目標(biāo)函數(shù)的維數(shù),,T為最大迭代次數(shù)。時(shí)間復(fù)雜度如表1所示,。

2 BAIWO算法仿真實(shí)驗(yàn)
2.1 實(shí)驗(yàn)的初始參數(shù)設(shè)置
該算法的最優(yōu)參數(shù)設(shè)計(jì):初始種群個(gè)體M0=30,,最大種群個(gè)體Max=50,最大種子數(shù)為Smax=5,,最小種子數(shù)為Smin=2,,調(diào)和指數(shù)n=3,,方差最大值和最小值分別為10和0.001,,最大響度A=0.25,最大脈沖率R0=0.5,,脈沖響度范圍為[0,,2],脈沖衰減系數(shù)為0.9,;6個(gè)不同的測試函數(shù)[11]f1~f6最大迭代次數(shù)分別為500,,500,200,,500,,500,500,。函數(shù)參數(shù)如表2所示,。

2.2 測試函數(shù)
在本實(shí)驗(yàn)中選取了6個(gè)標(biāo)準(zhǔn)測試函數(shù)分別對標(biāo)準(zhǔn)雜草算法和改進(jìn)后雜草算法進(jìn)行性能測試。
?。?)Sphere函數(shù)

上述6個(gè)基準(zhǔn)測試函數(shù)中,,除了f1是單峰函數(shù)以外,其余的都是多峰函數(shù),。圖1和圖2分別是應(yīng)用Rastrigin函數(shù)和Griewank函數(shù)對這兩種算法在不同迭代次數(shù)下測試所得到的收斂曲線,。

2.3 仿真結(jié)果分析
通過以上函數(shù)優(yōu)化測試曲線可以看出,在迭代初期,BAIWO算法相較于標(biāo)準(zhǔn)IWO算法就具有較好的收斂效果,,隨著迭代次數(shù)的增加,,到達(dá)迭代后期時(shí),BAIWO算法也能得到更好的收斂值,。說明改進(jìn)后的算法提高了標(biāo)準(zhǔn)IWO算法的性能,。
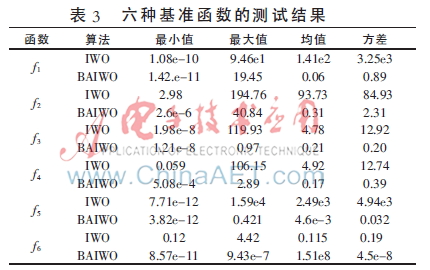
實(shí)驗(yàn)結(jié)果如表3所示,可以看出,,無論在單峰還是多峰函數(shù)下,,改進(jìn)后算法結(jié)果都優(yōu)于IWO算法,在求解函數(shù)f1(x)~f6(x)時(shí),,改進(jìn)后的算法都能獲得精確度較高的最優(yōu)值,,以及較好的平均值和方差。而IWO算法在求解這6個(gè)函數(shù)時(shí),,起始值較大,,收斂速度很慢,很容易陷入局部最優(yōu)解,??傮w而言,改進(jìn)后的算法能夠獲得與理論值較近的值,,以及很好的魯棒性,。
3 結(jié)束語
本文針對雜草算法存在早熟現(xiàn)象和易陷入局部最優(yōu)解等缺點(diǎn),提出了利用蝙蝠算法中回聲定位原理來對種群個(gè)體進(jìn)行更新,。從而使得種群前期擁有很好的全局收斂特性,,后期可以使其避免陷入局部最優(yōu)。從仿真結(jié)果看出,,BAIWO算法在很大程度上提高了雜草算法的收斂性和尋優(yōu)精度,。然而,如何改變IWO算法中種群多樣性來提高它的收斂性是今后要進(jìn)一步研究的方向,。
參考文獻(xiàn)
[1] 張氫,,陳丹丹,秦仙蓉,,等.雜草算法收斂性分析及其在工程中的應(yīng)用[J].同濟(jì)大學(xué)學(xué)報(bào)(自然科學(xué)版),,2010,38(11):1689-1693.
[2] 彭斌,,胡常安,,趙榮珍.基于混合雜草算法的神經(jīng)網(wǎng)絡(luò)優(yōu)化策略[J].振動,測試與診斷,,2013,,33(4):634-639.
[3] HAJIMIRSADEGHI H,, LUCAS C.A hybrid IWO/PSO algorithm for fast and global optimization[J]. IEEE EUROCON 2009. Piscataway: IEEE, 2009:1964-1971.
[4] Zhang Xuncai,,Niu Ying,, Gui Gangzhao, et al. A modified invasive weed optimization with crossoever operation[C]. The 8th world Congress on Intelligent Control and Automation,,2010:11-14.
[5] 張玉,,蔣海榮,胡進(jìn),,等.基于改進(jìn)雜草優(yōu)化算法的DFCW參數(shù)估計(jì)[J].現(xiàn)代雷達(dá),,2013,35(7):20-23.
[6] 賈盼龍,,田學(xué)民.基于自適應(yīng)小生境的改進(jìn)入侵性雜草優(yōu)化算法[J].上海電機(jī)學(xué)院學(xué)報(bào),,2012,15(4):225-231.
[7] Yang Xinshe. Nature-inspired Metaheuristic Algorithms[M]. Beckington: Luniver Press,, 2010.
[8] 李枝勇,,馬良,張惠珍.蝙蝠算法收斂性分析[J].數(shù)學(xué)的實(shí)踐與認(rèn)識,,2013,,43(12):182-191.
[9] 肖輝輝,段艷明.基于DE算法改進(jìn)的蝙蝠算法的研究以及應(yīng)用[J].計(jì)算機(jī)仿真,,2014,,31(1):272-280.
[10] 陳歡,周永權(quán).入侵雜草算法的改進(jìn)分析及研究[D].南寧:廣西民族大學(xué),,2013.
[11] MEHRABIA A R,, LUCAS C. A novel numerical optimization algorithm inspired from weed coloniz[J]. Ecological Information,, 2006,,1(4):355-366.

