摘  要： 增量式數(shù)字PID是自動控制系統(tǒng)優(yōu)化過程中應(yīng)用廣泛的一種控制方法,。分析了增量式PID參數(shù)調(diào)節(jié)對控制器性能以及系統(tǒng)環(huán)路性能的影響,。MATLAB頻域仿真結(jié)果表明，Kp,、Kd,、Ki值的改變直接造成PID控制器零點(diǎn)的位置發(fā)生移動，從而使得控制系統(tǒng)動態(tài)性能得到改善,。

　　關(guān)鍵詞： 增量式數(shù)字PID,；參數(shù)調(diào)節(jié)；頻域分析

0 引言

　　計算機(jī)控制系統(tǒng)的核心是數(shù)字調(diào)節(jié)器,，工程中常用的數(shù)字調(diào)節(jié)器控制方法有以下幾種：（1）直接數(shù)字控制：根據(jù)采樣理論和離散化后的數(shù)字模型設(shè)計數(shù)字控制器,，該方法的前提是得到系統(tǒng)的數(shù)字模型；（2）比例-積分-微分（propotional-integral-derivative,，PID）控制：調(diào)節(jié)器的輸出是其輸入的比例,、積分和微分的函數(shù)，特點(diǎn)是不需要被控對象的數(shù)字模型,，結(jié)構(gòu)簡單,、穩(wěn)定可靠，故工程應(yīng)用廣泛,；（3）最優(yōu)控制：基于性能指標(biāo)J最小的控制策略（燃料最省,、路徑最短、時間最短）,，依賴于對象的數(shù)字模型,；（4）智能控制：包括神經(jīng)網(wǎng)絡(luò)、模糊控制等,，基于仿人類思維的模糊數(shù)據(jù)推理方法,，不需要數(shù)字模型，但控制算法復(fù)雜,。

1 增量式PID算法的數(shù)字實(shí)現(xiàn)

　　數(shù)字PID控制系統(tǒng)是時間的離散系統(tǒng),，Proportional（比例）,、Integral（積分）、Differential（微分）可根據(jù)系統(tǒng)的要求,，對輸入的偏差按比例、積分和微分的函數(shù)關(guān)系運(yùn)算得到控制量,，輸出到執(zhí)行器完成相應(yīng)的調(diào)節(jié)任務(wù)[1],。在PID調(diào)節(jié)中，由于PID算式可以靈活地改變其結(jié)構(gòu),，因此選擇不同的P,、I、D會得到不同的控制效果,，特別是當(dāng)算法中某些參數(shù)選擇不當(dāng)時,，會引起控制系統(tǒng)的超調(diào)或振蕩，這對某些生產(chǎn)過程是十分有害的[2],。為了避免這種有害現(xiàn)象的發(fā)生,，分析和研究PID算法，確定合理的PID參數(shù)是必要的,，同時對PID控制技術(shù)的廣泛應(yīng)用具有重要的意義,。

　　PID算法的模擬表達(dá)式如式（1）所示：

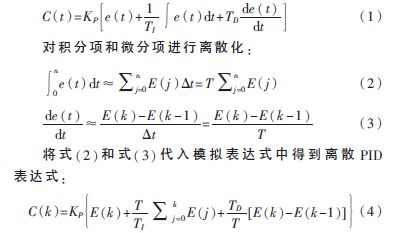
　　上式的輸出與系統(tǒng)位置一一對應(yīng)，也稱為位置型PID算式,。用位置型PID算式計算C（K）,，需要用到各采樣時刻的偏差值，計算復(fù)雜,，且需要占用內(nèi)存,。

　　對于系統(tǒng)（k-1）時刻的輸出：

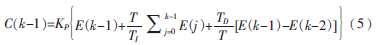
　　將式（4）、式（5）相減后得到如下表達(dá)式：

　　C（k）-C（k-1）=KP[E（k）-E（k-1）]+KIE（k）+

　　KD[E（k）-2E（k-1）+E（k-2）]（6）

　　式（6）表示第k次輸出的信號增量,，稱為增量型PID控制算式,。

　　位置型算式不僅需要對E（j）進(jìn)行累加，而且計算機(jī)的任何故障都將引起C（k）的大幅度變化,，對生產(chǎn)不利,。增量型較位置型的優(yōu)點(diǎn)如下：（1）由于輸出的是增量，所以誤動作??；（2）易于實(shí)現(xiàn)手動/自動的無擾切換（位置型算法中，當(dāng)由手動切換到自動時,，首先需要保證控制器的輸出等于實(shí)際的控制量,；增量型算式只給出偏差，而與原來位置無關(guān)）,；（3）不產(chǎn)生積分失控,，容易獲得良好的調(diào)節(jié)品質(zhì),。

2 增量型PID參數(shù)調(diào)節(jié)對控制器的性能影響

　　對于增量型PID數(shù)字控制策略，為了便于分析其對系統(tǒng)性能的影響,，將差分方程進(jìn)行Z變換得到脈沖函數(shù),，如式7所示：

　　從校正系統(tǒng)的傳遞函數(shù)中可以簡單地看出Kp、KI,、KD,、T均與控制器的零點(diǎn)相關(guān)。

　　2.1 Kp變化對幅值相位的影響分析

　　根據(jù)增量式PID的傳遞函數(shù)編寫MATLAB命令如下：

　　kp=0.002*32*1023/3.3*2.49/10.36/3300,；

　　ki=0.002*32*1023/3.3*2.49/10.36/3300,；

　　kd=0.002*32*1023/3.3*2.49/10.36/3300；

　　fs=（150e3）,；

　　a=tf（[kd/fs kp ki*fs],，[10]）；

　　a1=tf（[kd/fs kp*100 ki*fs],，[1 0]）,；

　　a2=tf（[kd/fs kp/100 ki*fs]，[1 0]）,；

　　bode（a,，′-′，a1,，′--′,，a2，′.-′）,；

　　a中Kp采用標(biāo)準(zhǔn)值,，a1中Kp值增大為a中Kp值的100倍，a2中Kp值減小為a中Kp值的百分之一,。MATLAB仿真畫出PID校正裝置相應(yīng)的Bode圖,，如圖1所示。

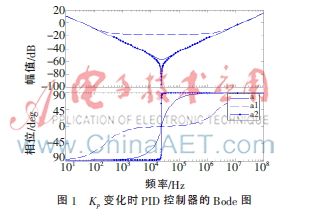
　　從圖1可以明顯看出,，隨著Kp增大,，PID控制器兩個零點(diǎn)逐漸分離，且起始增益無明顯變化,；反之,，Kp減小，兩個零點(diǎn)向中間靠攏,。

　　2.2 KI變化對幅值相位的影響分析

　　MATLAB仿真時,，a采用KI標(biāo)準(zhǔn)值，a1中KI值增大為a中KI值的100倍，a2中KI值減小為a中KI值的百分之一,，相應(yīng)的Bode圖如圖2所示,。

　　從圖2可以明顯看出隨著KI增大（a2→a→a1），零極點(diǎn)右移,，左邊零點(diǎn)右移,，最終兩個零點(diǎn)同時右移，起始增益明顯增加,；反之,，KI減小（a1→a→a2）,，零極點(diǎn)左移，左邊零點(diǎn)左移,，起始增益明顯減小,。

　　2.3 KD變化對幅值相位的影響分析

　　MATLAB仿真時，a采用KD標(biāo)準(zhǔn)值,，a1中KD值增大為a中KD值的100倍,，a2中KD值減小為a中KD值的百分之一，相應(yīng)的Bode圖如圖3所示,。

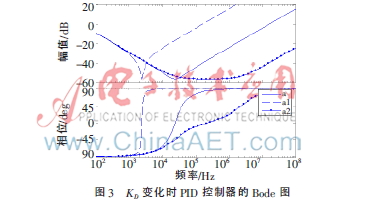
　　從圖3可以明顯看出,，隨著KD增大（a2→a→a1），右邊零點(diǎn)左移,，最終兩個零點(diǎn)同時左移,，起始增益無明顯變化；反之,，KD減?。╝1→a→a2），右邊零點(diǎn)右移,。

3 PID參數(shù)調(diào)節(jié)對系統(tǒng)穩(wěn)定性能的影響分析

　　為了進(jìn)一步分析PID參數(shù)調(diào)節(jié)對系統(tǒng)性能的影響,，本文以Buck變換器在電阻性負(fù)載下的傳遞函數(shù)模型為例進(jìn)行說明。

　　3.1 Buck變換器的小信號模型

　　Buck變換器閉環(huán)控制系統(tǒng)如圖4所示,。

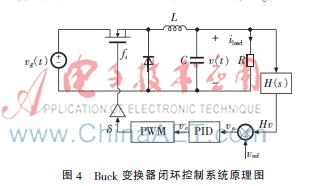
　　Buck變換器工作在連續(xù)電流模式（CCM）下,，其小信號傳遞函數(shù)如式（10）所示：

　　3.2 Kp變化對系統(tǒng)性能的影響分析

　　帶PID控制器的Buck變換器系統(tǒng)的開環(huán)傳遞函數(shù)為：

　　G（s）=GC（s）Gvd（s）

　　MATLAB仿真時，Buck變換器取如下參數(shù)：Vg=50/4 V,，L=0.24 H,，RDCR=0.7 Ω，C=330 F,，RESR=0.1 mΩ,，R=10 Ω；G采用Kp標(biāo)準(zhǔn)值,，G1中Kp值增大為G中Kp值的10倍,，G2中Kp值減小為G中Kp值的十分之一,，仿真得到系統(tǒng)的Bode圖如圖5所示。

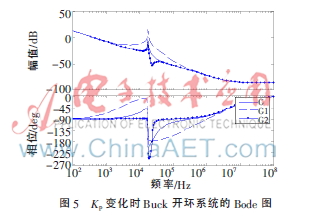
　　從圖中可以明顯看出,，隨著Kp減?。℅1→G→G2），系統(tǒng)諧振峰值減小,，有利于系統(tǒng)的平穩(wěn)性,，但系統(tǒng)相位裕量會減小甚至出現(xiàn)負(fù)值，從而導(dǎo)致系統(tǒng)不穩(wěn)定,。

　　3.3 KI變化對系統(tǒng)穩(wěn)定性能的影響分析

　　G采用KI標(biāo)準(zhǔn)值,，G1中KI值增大為G中KI值的10倍，G2中KI值減小為G中KI值的十分之一,，仿真得到系統(tǒng)的Bode圖如圖6所示,。

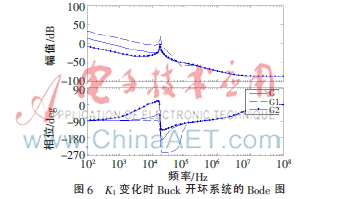
　　從圖中可以明顯看出隨著KI增大（G2→G→G1），系統(tǒng)相位裕量明顯減小,，并出現(xiàn)負(fù)值,，導(dǎo)致系統(tǒng)不穩(wěn)定，故在PID設(shè)計中KI系數(shù)雖然有利于消除靜差,，但仍不能取值太大,。

　　3.4 KD變化對系統(tǒng)穩(wěn)定性能的影響分析

　　G采用KD標(biāo)準(zhǔn)值，G1中KD值增大為G中KD值的10倍,，G2中KD值減小為G中KD值的十分之一,，仿真得到系統(tǒng)的Bode圖如圖7所示。

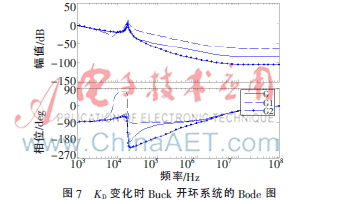
　　從圖中可以明顯看出,，隨著KD減?。℅1→G→G2），系統(tǒng)抗噪聲能力增強(qiáng),，但相位裕量會出現(xiàn)負(fù)值,，從而導(dǎo)致系統(tǒng)不穩(wěn)定。

4 結(jié)論

　　通過以上對數(shù)字增量式PID控制算法的分析與研究,，可得出PID參數(shù)調(diào)節(jié)對控制器本身性能的影響如下：

　?。?）Kp對增益影響不大，且Kp的增大導(dǎo)致兩個零點(diǎn)頻率分離,。

　?。?）KI對低端增益有影響操控，因?yàn)镵I增大,，零極點(diǎn)頻率增大,。同時，KI增大，左邊的零點(diǎn)右移,，當(dāng)左邊的零點(diǎn)達(dá)到右邊零點(diǎn)頻率時,，兩個零點(diǎn)同時右移。

　?。?）KD對增益影響不大,，且KD的增大導(dǎo)致右邊零點(diǎn)左移，當(dāng)右邊的零點(diǎn)達(dá)到左邊零點(diǎn)頻率時,，兩個零點(diǎn)同時左移,。

　　在對系統(tǒng)進(jìn)行增量式數(shù)字PID校正過程中，系統(tǒng)的穩(wěn)定性,、快速性,、平穩(wěn)性以及準(zhǔn)確性是相互矛盾、不能同時兼得的,，故應(yīng)根據(jù)實(shí)際情況合理選擇Kp,、KI、KD參數(shù)優(yōu)化系統(tǒng)性能,。尤其當(dāng)Kp、KD變小或KI值增大時,，系統(tǒng)相位裕量會出現(xiàn)負(fù)值,，從而導(dǎo)致系統(tǒng)不穩(wěn)定，在實(shí)際設(shè)計中應(yīng)注意避免,。

參考文獻(xiàn)

　　[1] 胡壽松．自動控制原理[M]．北京：科學(xué)出版社,，2013．

　　[2] 劉光亞，彭維娜．PID參數(shù)性能分析及改進(jìn)[J]．湖北工業(yè)大學(xué)學(xué)報,，2013,，28（1）：60-63．

　　[3] ERICKSON R W， MAKSIMOVIC D． Fundamentals of Power Electronics[M]． USA：Kluwer Academic Publishers,，2001.