0 引言

    近年來,，許多研究都集中于博弈論在資源分配和調(diào)度方面的問題^[1],，但博弈論不僅適合應用在這些問題上,，也可以應用在Web安全攻防問題上。Stackelberg博弈應用在Web安全問題中時,，領導者是信息安全人員,，而追隨者是黑客。隨著安全技術的提升,，有多種先進的策略和技術可以提供給攻擊者和防御者,。本文中要解決問題是尋找穩(wěn)定的Stackelberg博弈用于Web應用安全中領導者的最優(yōu)策略。本文提供了Stackelberg安全博弈和貝葉斯Stackelberg安全博弈的詳細描述,，對其在Web安全領域的適用性進行了討論,，并給出了實驗的結(jié)果。

    不同的研究者探索用博弈論的方法來建立安全問題的適用性^[1],，在過去的幾年有了顯著的結(jié)果和實際運用,。在文獻[2]中，提出了ARMOR框架,，能夠有效地在洛杉磯國際機場內(nèi)設置檢查點和警犬巡邏維護安全,。在文獻[3-4]中，博弈論被用于聯(lián)邦空警在商業(yè)航班中的安全護航,，以及在紐約地鐵中的逃票檢查,。博弈論也已經(jīng)被用在建立信息安全領域的模型中，文獻[5]用完全信息的靜態(tài)博弈來建立信息安全的攻防模型,。在文獻[6]中,，利用零和隨機博弈對攻擊者和系統(tǒng)管理員的行為進行建模，其中網(wǎng)絡被表示為一組獨立的節(jié)點來對應安全資產(chǎn)和漏洞,。在文獻[7-8]中,，描述了在信息安全問題中運用博弈論的方法找到最佳的策略，提出了相關決策的懲罰參數(shù),。在文獻[9]中,，提出了基于馬爾科夫決策過程的博弈模型對漏洞威脅進行風險評估。

    本文將會探討在Stackelberg博弈中防守者和攻擊者形成最優(yōu)穩(wěn)定局面可能性以及在Web安全領域的應用,。本文的目標是找到在Web安全問題中面對攻擊時最有效的防守策略,。

1 Stackelberg博弈

    Stackelberg博弈是非合作、有先后次序的決策博弈,。是由兩個局中人領導者和追隨者參與的一種博弈論類型,。被稱為領導者(leader)的參與者首先發(fā)布一個混合策略，另一個被稱為追隨者(follow)的參與者在領導者的策略下優(yōu)化自己的性能或收益,，回應一個純策略,。兩個參與者都想其收益最大化。每個參與者有一個可能的行動集合,，每個參與者可以從集合中選擇形成策略,，這個策略是參與者可能采取行動的概率分布,，可以表示參與者選擇這個行動的可能性。參與者只能選擇一個行動的策略就叫做“純策略”,。而在混合策略中每個行動可以被選擇的概率是0≤p＜1,。由于本文側(cè)重于Stackelberg博弈在安全領域中的應用，相關術語“領導者”對應的“防守者”及“追隨者”對應的“攻擊者”會被交替使用,。

1.1 貝葉斯Stackelberg博弈

    貝葉斯Stackelberg博弈將Stackelberg博弈擴展成允許有多個類型的追隨者,，每種類型都有其自己的收益矩陣，方便建立有多個類型攻擊者的模型,。在貝葉斯Stackelberg博弈中，追隨者的類型集合表示為{1,，2,，…，I},，其中每種類型1≤λ≤I都有一個先驗概率Pλ來表示其出現(xiàn)的可能性,。領導者在知道每種類型追隨者先驗概率分布的情況下承諾一個混合策略，但是領導者不知道面對的追著者的具體類型,。而追隨者會根據(jù)領導者的策略回應一個最佳的策略,。對于每個追隨者類型，領導者和追隨者對應的收益矩陣分別為U^λ和V^λ,。

1.2 穩(wěn)定Stackelberg均衡條件

    為了計算領導者的最優(yōu)策略,，則需要先定義穩(wěn)定Stackelberg均衡^[10]。首先需要定義一組向量函數(shù)g=(g¹,，g²,，…，g^I),，其中每個g^λ表示領導者的混合策略到λ類型追隨者的純策略的映射關系,，那么g(x)就是追隨者回應x策略的一組向量，可以表示為g(x)=(g¹(x),，…,，g^I(x))。

    定義1：對于給定一個收益矩陣為(U¹,，V¹),，…，(U^I,，V^I)類型的概率分布為p的貝葉斯Stackelberg博弈,，一組策略集(x，g)當且僅當滿以下條件時能構(gòu)成一個穩(wěn)定Stackelberg均衡,。

其中的所有j都是(2)中追隨者的最優(yōu)反應策略.

2 DOBSS算法

    在以前的研究中,，有很多方法可以用來解決Stackelberg安全博弈問題^[11],，DOBSS算法是其中一個能夠有效計算出在貝葉斯Stackelberg博弈中領導者的最優(yōu)混合策略。采用這個方法有3個優(yōu)勢,，首先這個方法不需要通過海薩尼轉(zhuǎn)換轉(zhuǎn)化為正則形式的博弈來表示貝葉斯博弈,；第二，該方法僅需計算一個混合整數(shù)線性規(guī)劃問題,，而不是計算一組線性規(guī)劃問題的集合,；第三，它直接搜索了領導者的最優(yōu)策略,，而不是Nash均衡,，從而使其能夠找到高回報的Stackelberg均衡策略(利用了領導者的優(yōu)勢)。

    首先需要定義一個基本形式來解決貝葉斯Stackelberg博弈問題,，這是一個混合整數(shù)二次規(guī)劃問題(MIQP),，其次會將其轉(zhuǎn)化為一個混合整數(shù)線性規(guī)劃的問題(MILP)。我們用x表示領導者的策略,，其由一組領導者的純策略向量組成,。xi的值表示純策略i在混合策略中的比例。同樣,，用q表示追隨者策略的向量,。我們用X和Q表示領導者和追隨者各自純策略的集合。M則是表示一個無窮大的正數(shù),。收益矩陣R和C的定義是：當領導者選擇純策略i,，追隨者選純策略j，R_ij是領導者的收益,，C_ij是追隨者的收益,。

    領導者的MIQP問題定義為：

    為了擴展這個Stackelberg模型來處理多個追隨者類型，我們遵循貝葉斯方法先假設存在一個先驗概率p^l來表示追隨者類型l出現(xiàn)概率,，用L表示追隨者類型的集合,。在這個例子中，q^l表示追隨者類型l∈L的策略向量,。同樣的,，領導者和追隨者類型為l的收益矩陣用矩陣R^l和C^l表示。那么領導者需要解決問題變?yōu)椋?/p>

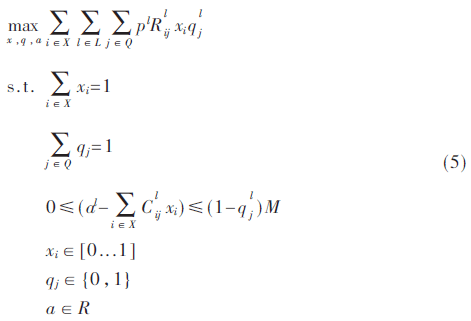
    這是我們可以在IBM的cplex框架下實施的最終形式,，將會在第4章討論,。

3 Stackelberg博弈在Web安全上的應用

3.1 Stackelberg博弈在Web安全上的適用性探討

    Stackelberg博弈在Web安全應用問題中非常有用。在這種情況下,，領導者可以是信息安全人員或者組織,，追隨者可以是黑客或者有組織的犯罪集團。領導者首先通過部署不同的信息安全策略來保護其資源，然后追隨者可以通過探測網(wǎng)絡確定其狀態(tài),，用純策略回應領導者的策略,。不同類型的追隨者可以被解釋為不同類型的攻擊，根據(jù)以前的研究和統(tǒng)計^[12],，安全部門可以構(gòu)建攻擊技術分布比例,，而攻擊者可以掃描網(wǎng)絡的當前狀態(tài)，查找漏洞,，實施最佳策略,。

    安全部門可以被當做一個領導者，原因如下：

    (1)在大多數(shù)情況下,，Web應用的安全策略是對外公開的,。

    (2)Web應用的安全手段和措施都是標準的和眾所周知的。黑客可以通過探測網(wǎng)絡來推斷安全部署,。而且這種信息經(jīng)常也可以從安全供應商得到,。

    (3)每個安全措施都有自己的弱點和不足，這給了攻擊者有機會選擇最好的方式來攻擊,。

    這些情況都可以說明Stackelberg策略可用在Web安全領域,。

3.2 Web應用中的攻擊策略和修補策略

    為了具體說明將Stackelberg博弈策略運用在Web安全應用中,，本文建立了在Web安全應用中的攻防模型,。在Web應用安全問題中，攻擊者（跟隨者）試圖利用一些漏洞來執(zhí)行未經(jīng)授權(quán)的操作,，而安全人員（領導者）試圖解決這些錯誤,。根據(jù)研究^[13]，Web應用中最廣泛的追隨者的攻擊策略和領導者的修補策略見表1,，這些攻擊手段和防御手段分別對應了追隨者的行動集合和領導者的行動集合,。

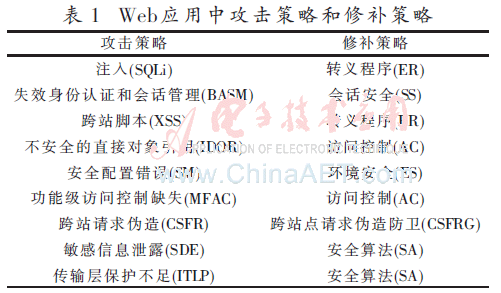
3.3 Web安全中領導者和追隨者的收益計算

    將Stackelberg博弈應用于Web應用的安全問題上，其核心問題是需要以一種有意義的方式填充領導者和追隨者的收益矩陣,。在研究[13]中,，OWASP團隊的文檔數(shù)據(jù)由7家專業(yè)的應用安全公司提供。數(shù)據(jù)涵蓋了來自上百家組織上千個應用,，超過500 000個漏洞,。根據(jù)這些數(shù)據(jù)，同時考慮攻擊向量的可利用性,、安全漏洞的普遍性和可檢測性以及技術影響的嚴重性程度等多方面因素,，給出了Web漏洞每個風險因素的風險值。在研究[13]的基礎上,，本文給出了Web安全應用中領導者修補策略的收益(表2)和追隨者攻擊策略的收益（表3）,。

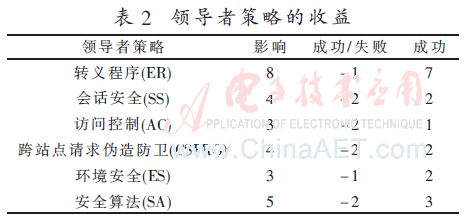
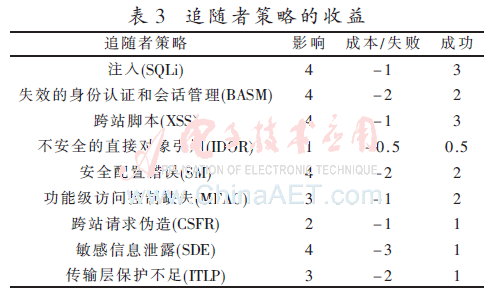
    根據(jù)收益表格，當追隨者發(fā)起攻擊時給出定義：

    (1)如果修補手段對攻擊手段是有效的，那么領導者的收益為領導者行動的影響減去領導者修補手段的成本,，追隨者的收益是其攻擊手段的成本,。

    (2)如果修補手段對攻擊手段是無效的，那么領導者的收益是負的,，其值為領導者修補手段的成本減去追隨者攻擊手段的影響,，追隨者的收益為追隨者行動的影響減去追隨者攻擊手段的成本。

    (3)追隨者同樣可以選擇不進行攻擊,，那么領導者的收益為其修補手段的成本,，追隨者的收益為0，由此可以得到收益表格來定義收益矩陣（表4）,。

4 實驗結(jié)果

    在本文實驗中使用了IBM ILOG CPLEX軟件來處理尋找Stackelberg博弈領導者的最優(yōu)策略時面臨的線性規(guī)劃問題,，IBM ILOG CPLEX是一種非常強大的線性規(guī)劃處理工具，支持各種編程語言,，在這個例子中,，我們使用JAVA語言編程實現(xiàn)。

    在這個例子中,，定義了兩種類型的追隨者,，它們的攻擊手段相同時具有相同的收益值，但是有不同的行動集合,。其中A類型的追隨者可以用第3章表1里攻擊策略集合中的任何純策略,，但是不可以不進攻(選擇NA策略)。而B類型的追隨者不可以使用SQLi和ITIP策略,。A類型的追隨者先驗概率為0.7,，B類型的追隨者先驗概率為0.3.

    得到程序的結(jié)果如下：

    優(yōu)化狀態(tài) :  Optimal

    領導者最大預期效用 :  -0.702 052 238 805 969 8

    A類型追隨者最大預期效益: 1.357 142 857 142 857 2

    B類型追隨者最大預期效益: 1.283 582 089 552 239

    追隨者的追策略：

    A的純策略: SQLi

    B的純策略: XSS

    領導者的混合策略：

    采取轉(zhuǎn)義程序行動的概率: 0.390 485 074 626 865 66

    采取會話安全的概率: 0.221 641 791 044 776 13

    采取訪問控制行動的概率: 0.0

    采取跨站點請求偽造防衛(wèi)行動的概率：0.166 231 343 283 582 05

    采取環(huán)境安全行動的概率: 0.221 641 791 044 776 05

    采取安全算法行動的概率: 0.0

    上述結(jié)果與研究[13]中的Web應用安全的研究情況相符，SQLi和XSS是威脅性最大的攻擊手段,，因此基于所得到的結(jié)果,，領導者可以使用如上的混合策略達到最優(yōu)防守狀態(tài)。

5 結(jié)論

    博弈論在安全領域有著越來越重要的作用,，近年來理論研究和生產(chǎn)實踐使安全博弈分析有了長足的發(fā)展[14],。本文綜述了貝葉斯Stackelberg博弈，在此基礎上提出了一種貝葉斯Stackelberg博弈策略在Web安全中的應用的模型,，綜合考慮領導者和追隨者的成本參數(shù)和收益參數(shù),，構(gòu)建了更加全面的局中人收益函數(shù)。并利用文獻[10]提出的DOBSS算法,，計算貝葉斯Stackelberg博弈均衡的混合整數(shù)二次規(guī)劃問題轉(zhuǎn)化為混合整數(shù)線性規(guī)劃問題,，并且借助了高性能的線性規(guī)劃問題處理工具CPLEX，給出實例計算了Web應用安全中防守者的最優(yōu)混合策略,。

    下一階段的工作將主要集中在兩個方面,。一方面,，雙方策略收益計算的精確性是一個亟待解決的問題，可以繼續(xù)研究提高收益函數(shù)計算的精確性,。另一方面,，在某些情況下防御者的策略是隨著威脅而變化的，可能加入信息收集工具,，將領導者和追隨者收益的數(shù)值進行實時更新,，采用動態(tài)博弈的理論進行研究。

參考文獻

[1] YOU X,，SHI Y Z.A kind of network security behavior model based on game theory[C].Proceedings of the Fourth International Conference on Parallel and Distributed Computing,，Applications and Technologies，2003.

[2] TAMBE M,，JAIN M,，PITA J A，et al.Game theory for security：key algorithmic principles,，deployed systems,，lessons learned[C].In 50th Annual Allerton Conference on Communication，Control,，and Computing,，2012.

[3] Yin Zhengyu，ALBERT X J,，MATTHEW P J,，et al.Sullivan：TRUSTS：Scheduling Randomized Patrols for Fare Inspection in Transit Systems[C].In Proceedings of Twenty-Fourth Conference on Innovative Applications of Artificial Intelligence(IAAI)，Toronto,，Canada,，July 2012.

[4] KORZHYK D,，YIN Z,，KIEKINTVELD C，et al.Stackelberg vs nash in security games-an extended investigation of interchangeability,，equivalence and Artificial Intelligence Research,，2011(4).

[5] JORMAKKA J，MOLSA J V E.Modeling information warfare as a game[J].Journal of Information Warfare,，2005,，4(2).

[6] NGUYEN K C，ALPCAN T,，BASAR T.Stochastic games for security in networks with independent nodes[J].Proceedings of International Conference on Game Theory for Networks(GameNets),，2009.

[7] SUN W，KONG X,，HE D,，et al.Information security investment game with penalty parameter[C].The 3rd International Conference on Innovative Computing Information and Control，2008.

[8] SUN W，KONG X,，HE D,，et al.Information security problem research based on game theory[C].International Symposium on Publication Electronic Commerce and Security，2008.

[9] C.Xiaolin,，T.Xiaobin,，YONG Z，et al.A Markov game theory-based risk assessment model for network information systems[C].International conference on computer science and software engineering,，2008.

[10] PARUCHURI P,，PEARCE J P，MARECKI J,，et al.Playing games with security：an efficient exact algorithm for bayesian stackelberg games[C].In Proc.of The 7th InternationalConference on Autonomous Agents and Multiagent Systems(AAMAS),，2008.

[11] Manish Jain，Christopher Kiekintveld,，Milind Tambe.Quality-bounded solutions for finite bayesian stackelberg games: scaling up[C].In The 10th Inter- national Conference on Autonomous Agents and Multiagent Systems-Volume 3,，AAMAS’11，pages 997-1004,，Richland,，SC，2011.International Foundation for Autonomous Agents and Multiagent Systems.

[12] Kaspersky Lab website[DB/OL].http：//www.kaspersky.com/.

[13] Jeff Williams,，Dave Wichers.OWASP Top 10 2013[DB/OL].https：//www.owasp.org/index.php/Top_10_2013,，2013.

[14] CONITZER V，SANDHOLM T.Computing the optimal strategy to commit to.In EC,，2006.