摘 要: 通過對上海洋山深水港口的船舶流量的調研以及對船舶交通流量影響因素的分析,,建立支持向量機預測模型,。同時為了解決支持向量機預測模型的參數(shù)選擇問題,引入了粒子群優(yōu)化算法進行參數(shù)優(yōu)化,,建立較優(yōu)的PSO-SVM預測模型,。通過MATLAB仿真實驗計算,將PSO-SVM模型與單純的SVM預測模型和灰色神經網(wǎng)絡預測模型結果進行對比分析,,證明了該模型的可行性和優(yōu)越性,。
關鍵詞: 船舶流量;多因素,;預測,;灰色神經網(wǎng)絡;支持向量機,;粒子群優(yōu)化算法
0 引言
船舶交通流量預測是將經濟預測技術和水運工程技術以及計算機技術有效地結合起來的一門涉及多門學科的新興應用科學,。船舶交通流量的預測相比于一般的市場預測及陸上交通預測等所要考慮的因素和指標要更為繁雜和復雜[1],對于數(shù)據(jù)采集處理要求更高,,這就要求在運用具體的方法時要因地制宜,。其中國內外學者用的較多的是人工神經網(wǎng)絡預測法及其組合預測法。但是人工神經網(wǎng)絡由于其容易陷入局部最小,、預測輸出隨機等問題,,從而降低了預測的精度,。
支持向量機(Support Vector Machine,,SVM)是一種新型的機器學習算法,它同樣以統(tǒng)計學理論為基礎,,以嚴格的數(shù)學理論為背景,,因其簡單明了的幾何解釋以及較高的泛化能力,在解決小樣本問題時具有獨特的優(yōu)勢,。于此同時,,與人工神經網(wǎng)絡相比,其克服了神經網(wǎng)絡中經常出現(xiàn)局部最優(yōu)解以及學習時間長,、收斂速度慢等問題,。但支持向量機還存在一些不足,,如模型的預測精度受訓練學習參數(shù)選取的影響很大,如何選取參數(shù)至關重要,。因此,,選取合適的參數(shù)是支持向量機從理論走向實際應用的關鍵。本文基于粒子群(Particle Swarm Optimization,,PSO)算法的優(yōu)勢,,用以對支持向量機難以確定的參數(shù)進行優(yōu)化,進而建立起PSO-SVM預測模型用以上海洋山深水港交通流量的預測,。
1 主要影響因素分析
船舶交通流量是經濟,、社會、政治,、技術發(fā)展對水運交通需求的具體反應,。無論選用何種預測方法進行船舶交通流量預測,都必須從實際分析考慮所預測模型的影響因素,。影響船舶交通流量的因素非常繁雜,,以上海洋山深水港為研究對象,在綜合分析和查閱大量文獻的基礎上,,可以從經濟因素,、港口因素、船舶因素,、其他因素四個主要的方面去研究,。
經濟因素是影響未來船舶交通流量的最主要的因素,上海國際航運研究中心將宏觀綜合的經濟指標合理化為上海航運景氣指數(shù)[2],。船舶的貨運量是衡量和量化港口因素的主要指標,。同時,伴隨著經濟貿易和造船技術的發(fā)展,,船舶越來越向著大型,、自動、快速,、專業(yè)化和標準化的方向發(fā)展,,考慮到衡量船舶因素的指標有很多,根據(jù)實際選擇需要選擇船舶平均噸位做為合適的指標,。另外,,經濟的變化總能體現(xiàn)在船舶交通流量上,而且呈現(xiàn)正比關系,,但是又有一定的滯后性,。所以根據(jù)實際情況考慮及數(shù)據(jù)處理的方便,對主要影響因素進行分析抽象、量化后選取上海航運指數(shù),、貨運量,、船舶的平均噸位[3]、七天前的流量4個因素作為主要因素預測上海洋山港船舶交通流量,。
2 船舶流量預測模型的構建
2.1 建立流量預測模型
根據(jù)上述主要影響因素構建船舶流量預測算法流程,,如圖1所示[4-7]。
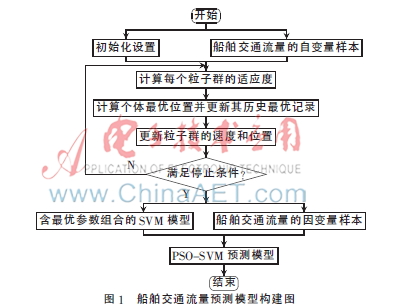
2.2 優(yōu)化支持向量機模型學習步驟
PSO優(yōu)化SVM的學習步驟如下[8]:
?。?)收集有關影響船舶交通流量的各種數(shù)據(jù),,分為因變量和自變量樣本;初始化各種參數(shù),,如粒子群規(guī)模,、初始位置和速度以及SVM的核函數(shù)、懲罰參數(shù)等,。
?。?)利用初始化后各粒子的數(shù)據(jù)值對因變量樣本進行學習和訓練并建立各自對應的預測模型。
?。?)通過對因變量樣本的學習訓練,,得到各個粒子的誤差值,用以計算各粒子的適應度函數(shù)值,,公式如下:

?。?)計算每個粒子的當前適應值F(Xi),并與該粒子當前自身的最優(yōu)適應值F(Pibest)進行比較,,如果F(Xi)<F(Pibest),,則調整F(Pibest)=F(Xi),將當前位置作為此刻該粒子的最優(yōu)位置,。
?。?)將每一個粒子自身當前最優(yōu)位置的適應值 F(Pibest)與所有粒子當前最優(yōu)位置的適應值F(Pgbest)進行比較,若F(Pibest)<F(Pgbest),,則調整F(Pgbest)=F(Pibest),,將調整后的位置做為所有粒子的最優(yōu)位置。
?。?)利用PSO的進化方程調整粒子的速度和位置,,進而得到支持向量機的參數(shù)。
?。?)判斷所有粒子最優(yōu)位置的適應值或迭代次數(shù)能否滿足要求,,若滿足,,則停止計算,,并保存此時的粒子群的整體最優(yōu)位置;若不滿足,,則返回步驟(2),。
?。?)將最優(yōu)參數(shù)代入支持向量機模型,對樣本進行有效預測,。
3 仿真實驗及結果分析
3.1 實驗數(shù)據(jù)及實驗設置
以上海洋山深水港進出的船舶為研究對象,,利用上海國際航運研究中心和上海洋山深水港統(tǒng)計的數(shù)據(jù),選取從2014年5月20日~2014年6月29日的船舶交通流量數(shù),、當日的上海航運指數(shù),、轉運量、船舶平均噸位作為自變量,,將2014年5月21日~2014年6月30日,,當天船舶流量數(shù)據(jù)作為因變量,建立預測模型對2014年5月21日~2014年6月30日每日的船舶流量數(shù)進行回歸擬合預測,。在實驗仿真之前首先得將所采用的流量數(shù)據(jù)進行歸一化處理,,采用的歸一化處理公式為:
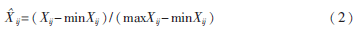
式中,j為歸一化后的數(shù)據(jù),;Xij為原始數(shù)據(jù),;minXij和maxXij分別為原始數(shù)據(jù)中的最小值和最大值。
基于MATLAB語言編寫了PSO-SVM程序,,通過試算確定PSO的參數(shù)如下:粒子個數(shù)為20,;粒子維數(shù)為2;循環(huán)次數(shù)為200,;學習因子c1=1.5,,c2=1.7;參數(shù)C的搜索范圍為(0.1,,100),;參數(shù)?滓的搜索范圍為(0.1,1 000),。經過PSO優(yōu)化,,得到SVM的最優(yōu)參數(shù)C=0.1,利用最優(yōu)參數(shù)來建立SVM模型,,進而對測試樣本進行預測,。
3.2 實驗仿真對比及分析
分別對灰色神經網(wǎng)絡模型、SVM模型,、PSO-SVM模型進行仿真并對比,,仿真結果見圖2~圖4。


對于預測結果需要通過定量的分析以確定精確度,,本文采用平均誤差和相對百分誤差來檢驗預測結果,。預測結果誤差如表1所示。
從圖2~圖4中可見,灰色BP神經網(wǎng)絡組合預測模型及SVM模型都得到不錯的效果,,但由于BP神經網(wǎng)絡樣本有時無法滿足要求,,存在過擬合現(xiàn)象及SVM參數(shù)選擇的問題,兩種算法的預測結果的準確性都受到很大影響,。PSO具有強大的全局搜索能力,,通過PSO優(yōu)化SVM模型的參數(shù),使其達到最優(yōu),,從而使誤差降到最低,。

從表1可以看出,PSO-SVM預測模型的平均誤差和相對百分誤差分別為1.653 6%和1.637 8%,,明顯小于灰色神經網(wǎng)絡預測模型和單純SVM預測模型的預測誤差,。因此,經PSO優(yōu)化的SVM模型比神經網(wǎng)絡預測模型以及SVM模型具有更好的預測能力,。
4 結束語
本文在考慮船舶影響因素的條件下,,利用SVM預測模型具有小樣本學習能力、學習速度快,、泛化能力強等優(yōu)點對船舶流量進行回歸預測,,并采用PSO優(yōu)化選擇SVM模型的參數(shù),得到較優(yōu)的SVM模型,,從而大大提高了預測的準確性和精度,。實驗結果表明,基于PSO-SVM的預測模型要好于單純的SVM預測模型,,該模型為船舶交通流量預測提供了新思路及有效方法,。
參考文獻
[1] 陳崇云.我國水上交通運輸安全分析及事故預測的研究[D].大連:大連海事大學,2002.
[2] 王東,,熊錫龍.基于影響因素分析的船舶交通流量預測多元線性回歸模型[J].船海工程,,2010,39(3):178-180.
[3] 李俊,,徐志京,,唐貝貝.基于GA優(yōu)化的灰色神經網(wǎng)絡船舶交通流量預測方法研究[J].船海工程,2013,,42(5):135-137.
[4] 馮宏祥,,肖英杰,孔凡邨,,等.基于支持向量機的船舶交通流量預測模型[J].中國航海,,2011,34(4):62-66.
[5] 任洪娥,,霍滿冬.基于PSO優(yōu)化的SVM預測應用研究[J].計算機應用研究,,2009,,26(3):867-869.
[6] 王樹洋,黃天民,,方新,等.基于PSO-SVM的交通流量短時預測[J].重慶交通大學學報(自然科學版),,2012,,31(4):832-835,872.
[7] 李紅喜,,付玉慧,,張仁初,等.港口船舶交通流量預測[J].大連海事大學學報,,2009,,35(3):40-42.
[8] 閆冠勇.基于PSO-SVM的CFG樁復合地基質量預測研究[D].邯鄲:河北工程大學,2012.

