0 引言

    正交頻分復(fù)用(OFDM)技術(shù)是一種多載波調(diào)制技術(shù),，能極大地提高頻譜利用率,，非常有效地對抗頻率選擇性衰落和窄帶干擾。早期多載波調(diào)制技術(shù),，各個子載波采用固定碼率的調(diào)制方式,，整個通信系統(tǒng)的誤碼率(BER)取決于性能最差的子載波；而自適應(yīng)調(diào)制技術(shù)根據(jù)當(dāng)前信道的狀態(tài)(CSI),，自適應(yīng)調(diào)整各個子信道的傳輸比特數(shù)以及調(diào)制方式,，提升系統(tǒng)性能。

    現(xiàn)有自適應(yīng)調(diào)制算法,，可以依據(jù)優(yōu)化準(zhǔn)則分為三類：基于信道增益的貪婪算法^[1,，2]，以信道容量為基準(zhǔn)的算法^[3],，以誤碼率性能為基準(zhǔn)的算法^[4,，5]。

    在實際的無線通信系統(tǒng)中,，會更多地考慮算法所占用的運算資源和信令開銷,。為了進一步降低算法開銷，提出了基于子載波分組的自適應(yīng)調(diào)制算法,，以組為單位對子載波進行資源分配，但是,，已有的分組算法或固定分組,，無法適應(yīng)不同通信環(huán)境^[6]，或者動態(tài)分組依據(jù)過于簡單^[7],。

    本文提出一種全新的,、近似均勻的動態(tài)分組自適應(yīng)調(diào)制技術(shù)，根據(jù)信道增益,、噪聲強度和碼率確定動態(tài)分組依據(jù),，并以組為單位自適應(yīng)分配通信資源，在保證系統(tǒng)誤碼率性能的前提下,，極大地降低系統(tǒng)開銷,。

1 經(jīng)典算法分析

    在現(xiàn)有的自適應(yīng)調(diào)制算法中，以Hughes-Hartogs算法最接近理論最優(yōu)解,，它將每個子信道從0 bit開始計算,，采用貪婪算法,，每增加1 bit都找到所需功率增加最小的子信道，直到所有比特分配結(jié)束,。但該算法運算量過大,。

    Chow算法是一種次優(yōu)化的自適應(yīng)調(diào)制算法，依據(jù)信道容量作為標(biāo)準(zhǔn)為各個子載波分配比特數(shù),，按照下式對子載波比特數(shù)進行初始化：

    SNR(i),、E_i和|Hi|²分別表示第i個子載波的信噪比、發(fā)射功率和信道增益,，N₀表示噪聲功率,，Γ表示系統(tǒng)與香農(nóng)限的差距，γ_margin是通過有限迭代得到的一個接近最優(yōu)化的門限值,。

    Fischer算法以誤碼率性能作為優(yōu)化標(biāo)準(zhǔn),，第i個子載波上M-QAM調(diào)制的誤碼率表示為：

2 近似均勻動態(tài)分組自適應(yīng)調(diào)制算法

2.1 算法流程

    本文提出的近似均勻的動態(tài)分組自適應(yīng)調(diào)制算法流程示意圖如圖1所示。算法分為3個步驟：(1)依據(jù)信道估計信息(CSI),，動態(tài)確定分組數(shù)目,；(2)將所有子載波排序，并分配到各個子載波組之中,；(3)以組為單位,，進行自適應(yīng)調(diào)制，分配通信資源,。

2.2 動態(tài)確定分組數(shù)目

    根據(jù)式（1）可以看出,，在相同傳輸功率的前提下，子載波的信道增益每提高一倍,，子載波可分配的比特數(shù)加1,；根據(jù)式（2）可知，在保證誤碼率不變的情況下,，可以得到同樣的結(jié)論,。因此，本算法分組依據(jù)的參數(shù)α₁如式（3）所示：

式中：c₁=0.2,，c₂=1.6,。從式（4）可以看出，誤碼率與噪聲功率,、子載波比特數(shù)都成正相關(guān),，同時，在噪聲功率比較高的情況下,，更復(fù)雜的自適應(yīng)調(diào)制算法所帶來的增益效果并不明顯,，因此應(yīng)該通過降低算法開銷來提升算法性能，即減小分組數(shù)目。本算法分組依據(jù)的參數(shù)α₂如下式所示：

2.3 子載波分配

2.4 自適應(yīng)資源分配

    本算法的自適應(yīng)資源分配以誤碼率性能為優(yōu)化標(biāo)準(zhǔn),，與Fischer算法相比,，有如下改進：以組為單位的子載波比特計算；信道過差的子載波整體剔除,；剩余比特調(diào)整,。

    本文所述算法比特分配具體實現(xiàn)步驟：

進入步驟(5)；

    (5)對b_i進行量化,，b_Qi=round(b_i),，計算量化誤差Δb_i=b_Qi-b_i，總比特數(shù)R_total=Σb_Qi×m_i,；

    (6)調(diào)整剩余比特數(shù)：如果R_total=R_target,，結(jié)束比特分配；如果R_total>R_target,，進入步驟(7),；如果R_total<R_target，進入步驟(8),；

    (7)如果R_total-m_i>R_target,，找到最小的Δb_i，調(diào)整b_Qi=b_Qi-1,，R_total=R_total-m_i,，Δb_i=Δb_i+1；如果R_total-m_i<R_target,，找到最小的Δb_i,，記錄序號i和R_total-R_target，將第i組子載波內(nèi)的前R_total-R_target個子載波比特數(shù)減1,，結(jié)束比特分配,；

    (8)如果R_total+m_i<R_target，找到最大的Δb_i,，調(diào)整b_Qi=b_Qi+1,，R_total=R_total+m_i，Δb_i=Δb_i-1,；如果R_total+m_i>R_target，找到最大的Δb_i,，記錄序號i和R_target-R_total,，將第i組子載波內(nèi)的后R_target-R_total個子載波比特數(shù)加1，結(jié)束比特分配,。

3 仿真驗證及結(jié)果分析

    本節(jié)將對本文提出的算法進行仿真驗證,，并從自適應(yīng)調(diào)制算法的兩個指標(biāo)：算法復(fù)雜度和誤碼率性能來分析本文算法的優(yōu)越性。

3.1 算法復(fù)雜度分析

    算法復(fù)雜度是衡量自適應(yīng)調(diào)制算法是否有實用性的重要指標(biāo),，表1在理論上分析了Hughes-Hartogs算法,、Chow算法,、Fischer算法和本文算法的計算復(fù)雜度。

    表1中,，N表示總子載波數(shù),，M表示分組數(shù)目，MAX_count是Chow算法設(shè)定的最大迭代總次數(shù),，β是Fischer算法剔除不符合要求子載波的迭代次數(shù),，ε₁、ε₂,、ε₃表示3種算法比特調(diào)整次數(shù)（ε₃小于ε₁和ε₂）,。可以看出,，貪婪算法計算復(fù)雜度直接與比特總數(shù)R_target相關(guān),，而Chow算法和Fischer算法復(fù)雜度與子載波總數(shù)目N相關(guān)，計算復(fù)雜度大大下降,；本文算法計算復(fù)雜度和分組數(shù)目M相關(guān),，計算復(fù)雜度最低。尤其是考慮到實際通信系統(tǒng)中的信道估計誤差和信令開銷,，本文算法在OFDM系統(tǒng)整體開銷上,，有大幅度的降低。

3.2 誤碼率性能仿真驗證

    本節(jié)對系統(tǒng)的誤碼率性能進行仿真對比驗證,。仿真信道為Rayleigh信道,，系統(tǒng)為QAM調(diào)制，最高階調(diào)制方式為256QAM,，本文仿真假設(shè)為理想信道估計,。

    圖2是本文算法與Chow算法、Hughes-Hartogs算法誤碼率性能的對比,?？梢钥闯觯疚乃惴ㄔ谡`碼率性能上比較接近貪婪算法Hughes-Hartogs,，略優(yōu)于Chow算法,。

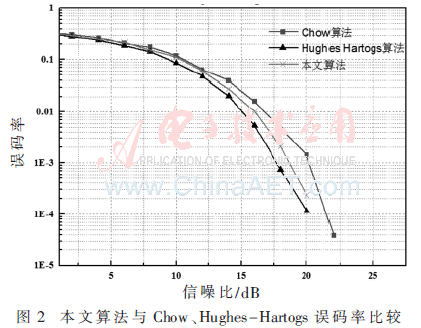
    圖3是本文算法與固定分組算法的對比，可以看出,，本文算法在誤碼率性能上更好,，而且本文算法自適應(yīng)動態(tài)確定分組數(shù)目，算法適用性更強,。

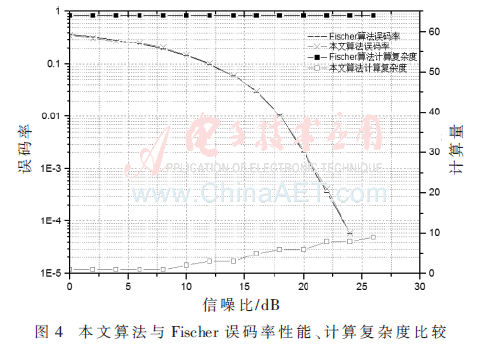
    圖4是本文算法與Fischer算法的誤碼率性能以及計算量的對比,。可以看出，本文算法誤碼率性能幾乎與Fischer算法相當(dāng),，但是計算開銷要遠(yuǎn)遠(yuǎn)低于Fischer算法,。

    綜合仿真結(jié)果可以得出本文算法的三個優(yōu)勢：(1)相對于已有的不分組自適應(yīng)調(diào)制算法，本算法在保證誤碼率性能的條件下,，大幅度降低運算量,；(2)相對于固定分組的自適應(yīng)調(diào)制算法，本算法誤碼率性能更好,，并且平均運算量更?。?3)本算法提出了更好的動態(tài)分組依據(jù),，對不同的信道環(huán)境的適應(yīng)性更強,。

4 結(jié)論

    本文針對OFDM系統(tǒng)中的自適應(yīng)調(diào)制領(lǐng)域進行了深入研究，提出了一種近似均勻的動態(tài)分組的自適應(yīng)調(diào)制算法,。算法復(fù)雜度分析和仿真結(jié)果表明,，該算法在誤碼率性能接近Fischer算法的同時，極大地減小了系統(tǒng)開銷,，并且該算法通過動態(tài)分組,，能適應(yīng)更復(fù)雜的通信環(huán)境。相對于已有的自適應(yīng)調(diào)制算法,，本算法性能更優(yōu)秀,，實用性更強。

參考文獻

[1] PRABHU R S,，DANESHRAD B.An energy-efficient water-filling algorithm for OFDM systems[C].Proceedings of the Communications(ICC),，2010 IEEE International Conference on，2010.

[2] HUGHES-HARTOGS D.Ensemble modem structure for imperfect transmission media[M].Google Patents,，1989.

[3] CHOW P S,，CIOFFI J M，BINGHAM J.A practical discrete multitone transceiver loading algorithm for data transmission over spectrally shaped channels[J].IEEE Transactions on communications,，1995,，43(234).

[4] WYGLINSKI A M，LABEAU F,，KABAL P.Bit loading with BER-constraint for multicarrier systems[J].Wireless Communications,，IEEE Transactions on，2005,，4(4).

[5] FISCHER R F,，HUBER J B.A new loading algorithm for discrete multitone transmission [C].Proceedings of the Global Telecommunications Conference，1996 GLOBECOM′96′Communications,，1996.

[6] LAI S K，CHENG R S，LETAIEF K B,，et al.Adaptive trellis coded MQAM and power optimization for OFDM transmission[C].Proceedings of the Vehicular Technology Conference,，1999 IEEE 49th，1999.

[7] LEE S-M,，PARK Y-S,，PARK D-J.Fast bit and power allocation algorithm for OFDM systems[C].Proceedings of the Vehicular Technology Conference，2004.

[8] YE S,，BLUM R S,，CIMINI JR L J.Adaptive OFDM systems with imperfect channel state information[J].Wireless Communications，IEEE Transactions on,，2006,，5(11).