摘  要： 植物學(xué)家提出的23種結(jié)構(gòu)定義了植物形態(tài)發(fā)生的方式和最終生長的形態(tài),，能夠形象而準(zhǔn)確地對植物形態(tài)發(fā)生進(jìn)行歸納和分類，但缺乏對植物形態(tài)可視化表達(dá)的有效手段和方法,。因此,，本文為再現(xiàn)植物的動態(tài)生長過程，基于構(gòu)筑模型,，遵循雙尺度自動機的基本原理,，應(yīng)用微分L-系統(tǒng)構(gòu)建植物連續(xù)生長過程的動態(tài)模型，并在計算機進(jìn)行了三維可視化實現(xiàn),。提出的方法拓展了構(gòu)筑模型的應(yīng)用,，仿真結(jié)果表明該方法在植物形態(tài)的建模上確實行之有效。

　　關(guān)鍵詞： 構(gòu)筑模型,；雙尺度自動機,；微分L-系統(tǒng)； 動態(tài),； 三維

0 引言

　　植物動態(tài)生長模型是指利用計算機形象直觀地再現(xiàn)植物生長過程,。在計算機建模時,，如何形象地體現(xiàn)植物的這種“生命”特征，使植物真正具有生長的現(xiàn)象已成為研究者廣泛關(guān)注的焦點,。因此，植物的模擬是在植物生長特征表達(dá)的基礎(chǔ)上實現(xiàn)從拓?fù)浣Y(jié)構(gòu)到幾何形態(tài)建模的過程[1],。植物學(xué)家以分類為目的,，提出的植物構(gòu)筑模型是指植物形態(tài)發(fā)生的方式以及最終長成的形態(tài)[2]。根據(jù)植物構(gòu)造模型可以在一個更高的層次上準(zhǔn)確地描述植物的結(jié)構(gòu)特點,，分析和模擬植物的生長過程,，該項研究被認(rèn)為是植物拓?fù)浣Y(jié)構(gòu)研究中的經(jīng)典工作[3]。

　　為了實現(xiàn)從拓?fù)浣Y(jié)構(gòu)到幾何形態(tài)建模的過程,，國內(nèi)外研究學(xué)者提出了多種植物建模方法,，其中以著名的L-系統(tǒng)的出現(xiàn)為標(biāo)志。最初的L-系統(tǒng)是D0L系統(tǒng),，它只能描述形狀規(guī)則的植物模型[4],。之后，加拿大學(xué)者Prusinkiewicz對L-系統(tǒng)進(jìn)行了擴(kuò)展,，提出開放L-系統(tǒng)（Open L-system）[5]和隨機L-系統(tǒng)（Stochastic L-system）[6]以及微分L-系統(tǒng)等[7],。在此期間又出現(xiàn)了基于分形理論的一系列植物建模方法，如疊代函數(shù)系統(tǒng)（IFS）,、分支矩陣,、粒子系統(tǒng)，以及由DeReffye提出的自動機模型（參考軸技術(shù)）和在此基礎(chǔ)上進(jìn)一步發(fā)展提出的雙尺度自動機模型等,。其中微分L-系統(tǒng)是一種發(fā)展得較完善的L-系統(tǒng)方法,，是參數(shù)L-系統(tǒng)的擴(kuò)展[8]。在該系統(tǒng)中,，產(chǎn)生式用于表達(dá)模型數(shù)量上的變化（比如植物新分支的產(chǎn)生）,，而微分方程求解過程則描述連續(xù)生長過程（比如莖的漸漸伸長）。雙尺度自動機模型是為了表現(xiàn)植物的生長機理,，由趙星等人從植物學(xué)的角度提出的,。盡管各種建模方法的目的和尺度不同，在建模原理和仿真的真實性要求上有很大的差異,，但在計算機建模時,，如何形象地體現(xiàn)植物的“生命”特征，使植物真正具有生長的現(xiàn)象已成為研究者共同關(guān)注的焦點,。

　　綜上可知,，構(gòu)筑模型能夠給出植物形態(tài)發(fā)生方式和最終形態(tài)，但并不能體現(xiàn)出植物生長過程的周期性,，且缺乏對植物形態(tài)可視化表達(dá)的有效手段和方法,，微分L-系統(tǒng)雖然可以進(jìn)行可視化表達(dá),，但其必須基于確定生長算法。因此本文在構(gòu)筑模型的基礎(chǔ)上進(jìn)一步引入雙尺度自動機原理,，給出更能表達(dá)植物真實生長過程的動態(tài)生長算法,，并使用微分L-系統(tǒng)進(jìn)行描述，最終形成一個基于構(gòu)筑模型的完整連續(xù)且具有周期性的動態(tài)發(fā)生模型,。

1 植物形態(tài)發(fā)生的基本原理

　　1.1 節(jié)周期,、生理周期

　　引用雙尺度自動機原理，勢必要用到描述植物周期的一系列概念,。下面將對之后要用到的周期性概念做出詳細(xì)的定義描述,。

　　植物的主體結(jié)構(gòu)由軸組成，植物的主干稱為主軸,；分枝用不同級的軸命名,，如1級側(cè)軸、2級側(cè)軸等,。如圖1所示,，軸上生葉的部位稱為節(jié)，節(jié)與節(jié)之間的那段軸稱為節(jié)間,。一般來說節(jié)和節(jié)間以及節(jié)上的側(cè)生器官（葉,、花或者果實）的集合，植物學(xué)上稱為植物分生單位,，長成一個新分生單位的時間稱之為節(jié)周期（Syllepticshoot）[10],。

　　另外，將枝條開始生長到產(chǎn)生分支之前的這段時間稱為一個生理周期,。每個生理周期包含若干個節(jié)周期,，節(jié)周期長短及每個生理周期包含節(jié)周期數(shù)視不同植物而定。在此,，選擇的Leeuwenberg模型的生長特征為：每個生長單元都生有花序,，而生長單元的生長就終止于花序，因此,，參考現(xiàn)在比較流行的觀點：將花朵看成一個節(jié)點縮短的變態(tài)短枝,。在對模型進(jìn)行周期性劃分時，特別將生殖生長階段作為一個單獨的節(jié)周期來處理[11],。

　　1.2 生長函數(shù)

　　植物生長動態(tài)模擬過程中,，對于植物量形成規(guī)律的描述，常需要借助于數(shù)學(xué)模型[12],。實驗中把節(jié)間生長的時間與生長長度的關(guān)系用直角坐標(biāo)圖來表示,，就會得到一條形狀像“S”的曲線，這條S曲線即為節(jié)間生長曲線,。進(jìn)一步的研究發(fā)現(xiàn)許多植物在其節(jié)周期內(nèi)的生長過程遵循這個模式,，為了得到一個最為合適的函數(shù)模型,，進(jìn)行了大量的研究。最終,，決定利用“S”型玻爾茲曼函數(shù)[13],，這個函數(shù)形式如下：

　　其中A是節(jié)間最大或最終長成后的尺寸，tm是當(dāng)其長到最大尺寸的一半時所用的時間,，k控制其相關(guān)的生長率,，也可以看作是特定的生長率。每一個生長模塊（如莖稈,、花朵、葉片）具有不同的生長速率,，因此需要使用不同的數(shù)學(xué)模型來描述（在此主要由不同的k值體現(xiàn)）,。例如大多數(shù)大戟科植物主干生長速率k為0.6±0.07d-1[10]，則其生長函數(shù)為：

　　對應(yīng)的線性圖像如圖2,。

　　由方程（1）所示的節(jié)間生長函數(shù)可知其微分形式為：

　　進(jìn)一步推導(dǎo)可得：

　　其中y是關(guān)于t的函數(shù),，代表生長函數(shù)，結(jié)合有限差分方法,，且在方程（4）中使用從t軸上等距抽樣得來的數(shù)值：tj=t0+jΔt（j=0,，1，…）,，并在區(qū)間[tn,，tn+1]中近似地使用差商代替微商，因此方程（4）最終可以寫為：

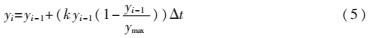
　　對于任意的i值,，可以將方程（5）看做分配一個新值yi到變量yi-1,，并在前鄰采樣點取值yi-1。t軸上的任意采樣點（除了邊界值）屬性作用類似,，因此方程（4）可以寫成L-系統(tǒng)產(chǎn)生式的形式：

　　上面僅僅是一部分,，而一個用于求解方程（2）的完整L-系統(tǒng)必須滿足：

　　（1）為m個模塊中的來自公理的M模塊創(chuàng)建一個初始字符串,；

　?。?）為變量y在每個模塊都設(shè)定一個初值；

　?。?）在模塊M的單步推導(dǎo)過程中維持變量y的初值和終值,。

2 構(gòu)筑模型

　　大千世界的植物種類繁多，為了便于歸納和分類,，植物學(xué)家給出下述四組簡單形態(tài)描述：（1）分支方式,；（2）軸的形態(tài)特征；（3）性特征位置,；（4）生長模式[14],。將其中的一組或者幾組進(jìn)行組合,，可以得到龐大的組合數(shù)目。然而在自然界僅發(fā)現(xiàn)23種植物構(gòu)造模型,，為了不額外增大植物學(xué)名詞量從而增加記憶負(fù)擔(dān),，每種構(gòu)筑模型都以植物學(xué)家的名字命名[2，9],。如Holttum模型,、Corner模型、Tomlinson模型等,。自然界中任何一種植物都可以由其中一種或者幾種模型組合進(jìn)行描述,。

　　本文主要研究大戟科植物，因此需要用Leeuwenberg模型描述,，該模型主要特點為合軸非線性分支,，每個模塊有兩個或多個分支，后繼模塊重復(fù)其父模塊的生長發(fā)育特點,，但是這個重復(fù)是定性的,，非定量的，表現(xiàn)為：后繼模塊的長度和分叉角度是遞減的,。圖3為植物學(xué)家給出的Leeuwenberg模型的圖形化描述,。

　　通過這些模型，植物學(xué)家不僅形象而又準(zhǔn)確地描述了各種類型植物的形態(tài)結(jié)構(gòu)特點,，而且進(jìn)一步研究了植物的生長過程及其生長規(guī)律,，這些結(jié)構(gòu)模型對樹木狀和草本狀植物都適用。因此,，利用植物的構(gòu)造模型,，對植物形態(tài)進(jìn)行仿真，不失為一種簡便快捷而又有效的方法[14],。

　　然而構(gòu)筑模型不能體現(xiàn)植物生長過程中表現(xiàn)出來的明顯周期性特性,，因此要結(jié)合雙尺度自動機原理得出更貼近植物真實生長過程的動態(tài)生長算法，這樣可以有效增強整個動態(tài)模型的真實感,。

3 微分L-系統(tǒng)

　　在對植物動態(tài)生長研究過程中,，尋找一種方法來對植物形態(tài)進(jìn)行可視化表達(dá)，從而建立更逼真,、完整,、有效的植物生長模型是必要的。在此選用微分L-系統(tǒng)進(jìn)行表達(dá),，它將傳統(tǒng)的L-系統(tǒng)產(chǎn)生式和微分方程合為一體,，成功模擬了植物生長過程中的離散、連續(xù)情況,。

　　微分L-系統(tǒng)是在參數(shù)化L-系統(tǒng)的基礎(chǔ)上,，通過引入連續(xù)的時間流的信息來取代一系列離散變換過程,，比如，模塊A（w）只要參數(shù)w的取值范圍在定義域DA中,，這個模塊就會連續(xù)地變化,，如果w的值達(dá)到了DA邊界，就會觸發(fā)一個產(chǎn)生式產(chǎn)生離散的變換,，這個時候A（w）就會被其子孫模塊替換[8],。

　　在t?琢?xí)r刻模塊A的結(jié)構(gòu)可以用一個連續(xù)的字符串表示：u=A1（w1）A2（w2）…An（wn）。其模塊增量的產(chǎn)生可能與其緊鄰的前后兩個模塊有關(guān)系,，也可能只與其中的某個模塊有關(guān),，也可能只與該模塊本身狀態(tài)有關(guān)。在此假設(shè)后一個模塊增量的產(chǎn)生只與其緊鄰的前一個模塊狀態(tài)有關(guān),，在此稱之為其左鄰居（沒有左鄰居的第一個模塊其w值為預(yù)先給出的定值）,，在上式中，Ai-1（wi-1）是Ai（wi）的左鄰居,，下面用l來指代A（w）的左鄰居。

　　A（w）模塊內(nèi)部的連續(xù)變化規(guī)律可以通過w關(guān)于時間t的微分方程來描述,，其微分方程為：

　　只要A（w）模塊中的參數(shù)w的取值范圍在A（w）的定義域DA中,，模塊就會根據(jù)上面的微分方程變化，DA是一個開區(qū)間,，CA是DA的邊界,，有m段互不相交的段組成，記為CA,。如果式子成立,，則用A（w）的子孫替換掉A（w），A（w）在時刻時的產(chǎn)生式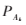：=A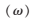：條件表達(dá)式→Bk,，1（wk,，1）Bk，2（wk,，2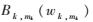）…,，其中A（w）稱為前驅(qū)，后面跟有條件表達(dá)式,，最后的Bk,，1（wk，1）Bk,，2（wk,，2）…稱為后繼，k可以取大于1的任意正數(shù)值表明以A（w）為前驅(qū)的產(chǎn)生式可能不止一個,，當(dāng)w到達(dá)不同區(qū)域的邊界時,，就使用不同的產(chǎn)生式,。

　　總之，微分L-系統(tǒng)通過把微分方程引入到參數(shù)L-系統(tǒng)中,，用來描述植物生長過程中的器官的連續(xù)變化性質(zhì),，是對參數(shù)L-系統(tǒng)進(jìn)行植物建模的擴(kuò)展。

4 植物的動態(tài)生長模型

　　為了快速有效地模擬大戟科植物動態(tài)生長過程中的生長細(xì)節(jié)和生長特性,，在Leeuwenberg模型的基礎(chǔ)上,，遵循雙尺度自動機原理對植物動態(tài)生長模型進(jìn)行構(gòu)建，其算法過程如圖4所示,。

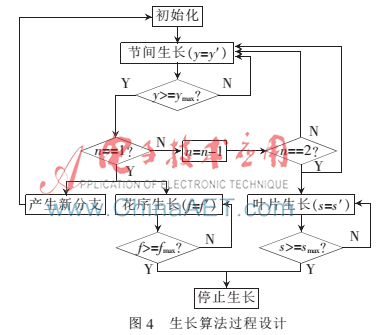
　　基于以上生長算法,，選用微分L-系統(tǒng)具體到每個節(jié)間的生長細(xì)節(jié)來模擬整個生長過程。為了實現(xiàn)這個目標(biāo),，設(shè)定每個節(jié)間長度,、葉片大小及花序大小的初值均大于0，其邊界值為定值,，在一個生理周期（包含n個節(jié)周期）內(nèi)節(jié)間長度一定,。

　　基于以上分析和假設(shè)最終形成的微分L-系統(tǒng)形式如下：

　　inital string：M（y0，s0,，f0,，n0，q0）

　　P1：M（y,，s,，f，n,，q）：y<ymax→M（y′,，s，f,，n,，q）

　　P2：M（y，s,，f,，n，q）：y>=ymax＆＆n>0→M（y0,，s,，f，n-1,，q）

　　P3：M（y,，s，f，n,，q）：s<smax＆＆n==2→M（y′,，s′，f,，n,，q）

　　P3：M（y，s,，f,，n，q）：n==1＆＆f<=fmax→F（y,，s,，f′，n,，q）

　　[+αM（qy,，qs，qf,，n0,，q）][-αM（qy，qs,，qf,，n0，q）]

　　其中：

　　q′=pq

　　將每個生理周期生長單元看作一個模塊M,，參數(shù)y代表節(jié)間的長度，s是葉片大小,，f是花序當(dāng)前生長量,，n為一個生理周期包含的若干個節(jié)周期。而其營養(yǎng)生長和生殖生長速率的不同用不同的k值界定（節(jié)間為k,，葉片為kl,，花序為kf）。p1主要是指節(jié)間從初始長度y0到最大長度ymax的連續(xù)生長過程,；p2指本節(jié)間生長完成進(jìn)入下一個節(jié)周期,；p3指在該生理周期的倒數(shù)第二個節(jié)周期內(nèi)同時進(jìn)行莖稈和葉片的生長；p4指本生長單元營養(yǎng)生長完成進(jìn)入生殖生長階段,；p5代表產(chǎn)生新的分支,；y′，f′,，s′方程主要管理節(jié)間,、花序和葉片具體生長節(jié)奏，一般約定y、f,、s初值恒為正數(shù),，p用于控制參數(shù)q的變化情況。

5 模型仿真

　　應(yīng)用該方法在VS2010+openGL環(huán)境下實現(xiàn)的Leeuwenberg模型在5個生理周期內(nèi)的生長細(xì)節(jié)如圖5,、圖6,、圖7所示。

6 結(jié)論

　　綜上所述,，模擬植物的真實動態(tài)生長過程,，應(yīng)該采用基于植物生長原理的模型（在此采用Leeuwenberg模型），因其能夠準(zhǔn)確描述植物生長過程及其生長規(guī)律,，而與雙尺度自動機原理的結(jié)合更有助于表達(dá)植物生長細(xì)節(jié)和生長特性,。另外，這種將參數(shù)L-系統(tǒng)與微分方程結(jié)合并綜合考慮了植物生長特征形成的新式微分L-系統(tǒng),，在表述植物生長過程時的主要優(yōu)點是：其可以將植物的生長過程細(xì)化到每個節(jié)周期,，而其中的參數(shù)可控性更是使處于不同生理周期的節(jié)間的不同生長特性得以體現(xiàn)。其能夠更加真實具體地反應(yīng)植物的動態(tài)生長過程,，尤其是“S”型玻爾茲曼函數(shù)的使用,，使得對于節(jié)間生長過程的模擬更加貼近真實。

參考文獻(xiàn)

　　[1] HONDA H,， HATTA H. Branch geometry in cornus kousa（Cornaceae）： computer simulation[J]. American Journal of Botany,， 1997，84（6）：745-755.

　　[2] HALLE F,， OLDEMAN R A A,， TOMLINSON P B. Tropical trees and forests： an architectural analysis[M]. Berlin： Springer Verlag， 1978.

　　[3] 趙星.忠實于植物學(xué)的虛擬植物生長研究[D].合肥：中國科技大學(xué),，2001.

　　[4] NDENMAY A. Mathematical models for cellular interaction in development,， parts I and II[J]. Journal of Theoretical Biology， 1968（18）：280-315.

　　[5] ,， PRUSINKIEWICZ P. Visual models of plants interacting with their environment[C]. Proceedings of the 23rd Annual Conferenceon Computer Graphics and Interactive Techniques,， 1996：397-410.

　　[6] PRUSINKIEWIEZ P， LINDENMAYER A. The algorithmic beauty of plants[M]. Spring-Verleg,， 1990.

　　[7] PRUSINKIEWICZ P,， FEDERL P， KARWOWSKI R,， et al. L-systems and beyond[J]. Course notes from SIGGRAPH,， 2003（5）：70-82.

　　[8] PRUSINKIEWICZ P， HAMMEL M,， MJOLSNESS E. Animation of plant development [J]. Computer Graphics,， 1993,，27（3）：351-360.

　　[9] DE REFFYE P， EDELIN C,，,， et al. Plant models faithful to botanical structure and development[C]. ACM SIGGRAPH Computer Graphics， 1988,， 22（4）： 151-158.

　　[10] 趙星,， DE REFFYE P，熊范倫,，等.虛擬植物生長的雙尺度自動機模型[J].計算機學(xué)報,，2001，24（6）：609-615.

　　[11] 敬松,，方逵,，陳演，等.圖像與L-系統(tǒng)相結(jié)合的柑橘葉片形態(tài)特征重構(gòu)研究[J].農(nóng)機化研究,，2012,，34（5）：65-67，71.

　　[12] 包鋼,，趙星,，閆紅平.植物生長建模與可視化—回顧與展望[J].自動化學(xué)，2001,，27（6）：816-835.

　　[13] ,， ERASMUS Y， LANE B,， et al. Quantitative modeling of arabidopsis development[J]. Plant Physiology,， 2005， 139（2）： 960-968.

　　[14] 丁維龍.虛擬植物生長模型及其與智能系統(tǒng)集成研究[D].合肥：中國科學(xué)技術(shù)大學(xué),，1999.