摘  要： 大數(shù)據(jù)時(shí)代悄然而至,，數(shù)據(jù)質(zhì)量也引起人們的關(guān)注,。在提高數(shù)據(jù)質(zhì)量方面，很重要的一部分是解決數(shù)據(jù)不一致性問題,。針對(duì)大數(shù)據(jù)情況下的數(shù)據(jù)不一致問題,，本文提出了在MAP-REDUCE框架下的聚類算法。本文在MAP-REDUCE框架下對(duì)K-MEDOIDS聚類算法進(jìn)行了改進(jìn),，增強(qiáng)了算法的適用性和精確性,，并通過仿真實(shí)驗(yàn)驗(yàn)證了在大數(shù)據(jù)環(huán)境下該算法的并行性和有效性。

　　關(guān)鍵詞： 大數(shù)據(jù),；數(shù)據(jù)質(zhì)量,；數(shù)據(jù)不一致性；MAP-REDUCE,；聚類算法

0 引言

　　隨著大數(shù)據(jù)時(shí)代的到來,，龐大的數(shù)據(jù)被賦予了新的生命，而數(shù)據(jù)質(zhì)量問題也引起了越來越多的關(guān)注,。數(shù)據(jù)質(zhì)量涉及數(shù)據(jù)的一致性,、正確性、完整性和最小性等多個(gè)方面[1-2],。當(dāng)分布在多個(gè)節(jié)點(diǎn)的數(shù)據(jù)集成時(shí),，若提供的數(shù)據(jù)出現(xiàn)重疊，容易引起數(shù)據(jù)不一致性的問題。如何從若干個(gè)不一致的數(shù)據(jù)中獲得理想的數(shù)據(jù)答案在數(shù)據(jù)清洗中就顯得至關(guān)重要[3],。

　　本文提出了基于MAP-REDUCE的聚類算法解決大數(shù)據(jù)環(huán)境中數(shù)據(jù)不一致性問題,。改進(jìn)了K-MEDOIDS聚類算法，提高了算法的適用性和精確性,。

1 相關(guān)工作

　　目前,，解決數(shù)據(jù)不一致性問題的方案很多，如參考文獻(xiàn)[4]討論了太陽黑子探測數(shù)據(jù)不一致性問題,，并提出了一種加權(quán)匹配技術(shù)減小數(shù)據(jù)的不一致性。針對(duì)數(shù)據(jù)復(fù)制時(shí)產(chǎn)生的數(shù)據(jù)不一致問題,，參考文獻(xiàn)[5]定義了不同版本數(shù)據(jù)的距離函數(shù),，以此消除復(fù)制數(shù)據(jù)時(shí)的不一致性。參考文獻(xiàn)[2]是通過屬性間的條件依賴（CFD）探測數(shù)據(jù)間的不一致性進(jìn)而進(jìn)行數(shù)據(jù)修復(fù),。然而,，當(dāng)數(shù)據(jù)量急劇增大時(shí)，現(xiàn)有的清洗算法將不再適用,。

　　在大數(shù)據(jù)環(huán)境下,，數(shù)據(jù)呈現(xiàn)規(guī)模性、多樣性,、高速性和價(jià)值性等多種特性[6],。聚類算法是研究分類問題的一種統(tǒng)計(jì)分析方法，基于MAP-REDUCE的聚類方法可以有效解決大數(shù)據(jù)環(huán)境中的一些問題,。神經(jīng)網(wǎng)絡(luò)[7],、貝葉斯網(wǎng)絡(luò)[8]等算法也都在MAP-REDUCE框架下實(shí)現(xiàn)了并行化。

　　K-MEDOIDS聚類算法介紹如下,。

　　算法1：K-MEDOIDS聚類算法

　　Initialize：Random k objects in D as medoids

　　Associate each object to the closest medoid

　　For each medoid m

　　For each non-medoid object o

　　Get DISi

　　Select the new medoid with the lowest distance

　　Repeat steps 2 to 6 until there is no change in the medoids

　　其中,，GetDis（Di，Dj）函數(shù)的功能是獲取對(duì)象Di和Dj之間的距離,。本文主要解決文本型數(shù)據(jù)的不一致性問題,，所以選擇文本的最小編輯距離函數(shù)，即Levenshtein距離,。

2 基于MAP-REDUCE的聚類算法

　　2.1 基于MAP-REDUCE的K-MEDOIDS算法

　　互聯(lián)網(wǎng)的進(jìn)步讓人們足不出戶就可以完成火車票,、汽車票、機(jī)票等的訂購,，享受網(wǎng)上購物的樂趣,，而這一切，也需要通過在各個(gè)網(wǎng)站注冊并保留個(gè)人身份信息,，包括網(wǎng)上銀行等,，才能完成這一系列操作。假設(shè)將這些網(wǎng)絡(luò)的身份信息匯總到一起,，就有可能出現(xiàn)數(shù)據(jù)不一致情況,，如表1所示,，T1~T7共7條含有身份證號(hào)和姓名的數(shù)據(jù)來自5個(gè)不同的網(wǎng)站，由于某些原因,，如拼寫錯(cuò)誤（T3,、T4、T6）,、字段截?。═5）等，產(chǎn)生了數(shù)據(jù)不一致問題?，F(xiàn)在定義一條數(shù)據(jù)的格式為<KEY,，VALUE>，如<ID,，NAME>,。數(shù)據(jù)集DATA含有n條數(shù)據(jù)：{DATA1，DATA2,，…,，DATAn}，即{<KEY1,，VALUE1>,，<KEY2，VALUE2>,，…,，<KEYn，VALUEn>},。DATA中的數(shù)據(jù)分布在不同的節(jié)點(diǎn)上,，當(dāng)數(shù)據(jù)集成時(shí)，利用MAP-REDUCE框架的MAP過程把具有相同KEY的數(shù)據(jù)分配到同一節(jié)點(diǎn)上,，就得到了具有相同KEY值的數(shù)據(jù)<KEY,，List<VALUE>>，如表2和表3所示,。

　　當(dāng)發(fā)現(xiàn)List<VALUE>中的數(shù)據(jù)不同時(shí)（表2,、表3），就出現(xiàn)了數(shù)據(jù)不一致情況,。若想在List<VALUE>中找到比較理想的數(shù)據(jù),，可以采用K-MEDOIDS聚類算法。

　　把K-MEDOIDS聚類算法應(yīng)用到MAP-REDUCE框架下,，算法如下,。

　　算法2：基于MAP-REDUCE的K-MEDOIDS算法

　　（1）Input：DATA

　　（2）Map（DATA）MAPDATA={<KEY1,，List<VALUE1>,，<KEY2，List<VALUE2>,，…}

　?。?）For each MAPDATA <KEY，List<VALUE>

　?。?）Get medoids by using K-MEDOIDS algorithm

　?。?）Get the max-count medoid

　　（6）Output：<KEY1,，VALUE1>,，<KEY2，VALUE2>,，…，<KEYm,，VALUEm>

　　首先,，通過MAP操作把數(shù)據(jù)集具有相同KEY值的VALUE聚集在一起。然后,，通過K-MEDOIDS算法把List<VALUE>中的數(shù)據(jù)分為K個(gè)類,，有效排除數(shù)量少但誤差過大的數(shù)據(jù)，對(duì)于數(shù)量較多且誤差較小的數(shù)據(jù),，取其對(duì)象最多的分類的中心點(diǎn)作為理想數(shù)據(jù),。

　　2.2 更加適用的E-MEDOIDS聚類算法

　　算法2中，首先設(shè)定分類個(gè)數(shù)為K,，然后取隨機(jī)值作為K個(gè)分類的中心點(diǎn),。但在具體應(yīng)用中，不容易確定K的具體取值,。針對(duì)此情況,，對(duì)K-MEDOIDS進(jìn)行了初步的改進(jìn)，提出了初始誤差值E,，以改進(jìn)聚類初始化時(shí)的中心點(diǎn)分布,。

　　算法3：基于MAP-REDUCE的E-MEDOIDS聚類算法

　　（1）Input：DATA{DATA1,，DATA2,，…，DATAn}

　?。?）Map（DATA）MAPDATA={<KEY1,，List<VALUE1>，<KEY2，List<VALUE2>,，…}

　?。?）For each MAPDATA<KEY，List<VALUE>

　?。?）M1=VALUE1

　?。?）For each non-medoid object o

　　（3）If GetDis（o,，medoids）>E,，M.Add（o）

　　（4）Associate each object to the closest medoid

　?。?）For each medoid m

　?。?）For each non-medoid object Di

　　（7）Get DISi

　?。?）If DISi=min（DIS）

　?。?）m=Di

　　（10）Repeat steps 11 to 16 until there is no change in the medoids

　?。?1）Get the max-count medoid

　?。?2）Output：<KEY1，VALUE1>,，<KEY2,，VALUE2>，…,，<KEYm,，VALUEm>

　　算法3與算法2的不同之處在于（8）~（10）行：首先選取List<VALUE>的第一個(gè)值作為第一個(gè)分類的中心點(diǎn)（M1）。然后遍歷余下的對(duì)象,，若此對(duì)象與所有分類的中心點(diǎn)距離均大于初始誤差值E,，則把此對(duì)象作為新類的中心點(diǎn)添加到Medoids中。算法3用若干分散的對(duì)象作為分類的中心點(diǎn)代替算法2中的隨機(jī)對(duì)象,，目的是讓中心點(diǎn)分布得更加離散,，聚類的速度也有所提高。而且用E代替K更適用于本領(lǐng)域,，同時(shí)還可以通過對(duì)初始誤差值E的設(shè)定控制每個(gè)分類的范圍,。

　　2.3 具有權(quán)重值的EW-MEDOIDS聚類算法

　　算法3中，把所有節(jié)點(diǎn)的數(shù)據(jù)視作等價(jià)的,，沒有權(quán)重大小的區(qū)別,。然而現(xiàn)實(shí)生活中并非如此。例如,，政府網(wǎng)站提供的數(shù)據(jù)往往比其他的網(wǎng)站具有更高的可信度,。因此,，在所有節(jié)點(diǎn)上加上權(quán)重值，以此表明此節(jié)點(diǎn)數(shù)據(jù)的可信度,。通過權(quán)重值的設(shè)置,，可以調(diào)整分類中心點(diǎn)的偏移，使得結(jié)果更加精確,，如表4所示,。

　　算法4：基于MAP-REDUCE的EW-MEDOIDS聚類算法

　　（1）Input：DATA

　?。?）Map（DATA）MAPDATA={<KEY1,，List<VALUE1>，<KEY2,，List<VALUE2>,，…}

　　（3）For each MAPDATA<KEY,，List<VALUE>

　?。?）M1=VALUE1

　　（5）For each non-medoid object o

　?。?）If GetDis（o,，medoids）>E

　　（7）M.Add（o）

　?。?）Associate each object to the closest medoid

　　（9）For each medoid m

　?。?0）For each non-medoid object Di

　?。?1）Get DISi with weight

　　（12）If DISi=min（DIS）

　?。?3）m=Di

　?。?4）Repeat steps 11 to 16 until there is no change in the medoids

　　（15）Get the max-count medoid

　?。?6）Output：<KEY1,，VALUE1>，<KEY2,，VALUE2>,，…，<KEYm,，VALUEm>

　　數(shù)據(jù)集D={D1,，D2，…Dn}來自若干個(gè)不同節(jié)點(diǎn),。通過評(píng)價(jià)節(jié)點(diǎn)的可信度,，人工設(shè)定節(jié)點(diǎn)的權(quán)重值分別為（W1,，W2，…,，Wn）,。這樣數(shù)據(jù)集D可以表示為{<D1，W1>,，<D2,，W2>，…,，<Dn,，Wn>}。算法3和算法2的不同之處在于（13）行,，即更新中心點(diǎn)時(shí),，權(quán)重值屬性參與了計(jì)算。

3 仿真實(shí)驗(yàn)

　　為了評(píng)估本文提出的算法的效率,、并行程度,，搭建了HADOOP平臺(tái)進(jìn)行實(shí)驗(yàn)。實(shí)驗(yàn)的編程語言采用Java語言,，在HADOOP平臺(tái)上實(shí)現(xiàn)算法1,、算法2和算法3。實(shí)驗(yàn)平臺(tái)包含6個(gè)節(jié)點(diǎn),，每個(gè)節(jié)點(diǎn)安裝有UBUNTU 14.10操作系統(tǒng),、HADOOP 2.4.0平臺(tái)，具有AMD 3.10 GHz雙核處理器和4 GB內(nèi)存,。

　　本實(shí)驗(yàn)數(shù)據(jù)要求文本型數(shù)據(jù),，而且其中部分?jǐn)?shù)據(jù)呈現(xiàn)錯(cuò)亂現(xiàn)象，因此采用人工生成的測試數(shù)據(jù)集,。具有權(quán)重值的EW-MODOIDS算法是在E-MEDOIDS算法的基礎(chǔ)上加上節(jié)點(diǎn)的權(quán)重值控制中心點(diǎn)的偏移,，因此只要權(quán)重值的設(shè)定符合實(shí)際情況，EW-MEDOIDS算法的精確性就大于無權(quán)重干預(yù)的K-MEDOIDS算法和E-MEDOIDS算法,，無需實(shí)驗(yàn)驗(yàn)證,。

　　3.1 單節(jié)點(diǎn)數(shù)據(jù)規(guī)模對(duì)運(yùn)行時(shí)間的影響

　　為了評(píng)估算法的運(yùn)行效率，生成100~1 000條不一致的數(shù)據(jù)分別用K-MEDOIDS算法和E-MEDOIDS算法（EW-MEDOIDS算法和E-MEDOIDS算法效率相當(dāng)）在單一節(jié)點(diǎn)實(shí)現(xiàn),。在生成單節(jié)點(diǎn)實(shí)驗(yàn)數(shù)據(jù)時(shí),，首先設(shè)置固定詞條作為正確答案，然后按一定比例隨機(jī)挑選數(shù)據(jù)條目進(jìn)行增加,、刪除,、修改、調(diào)換順序等操作,，每組實(shí)驗(yàn)數(shù)據(jù)均取十次相同重復(fù)實(shí)驗(yàn)結(jié)果的平均值,。

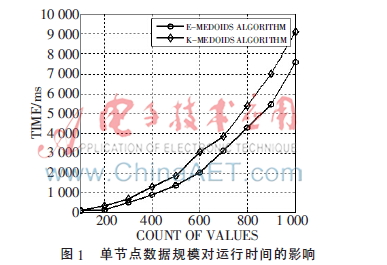
　　E-MEDOIDS算法中參數(shù)E的引入不僅提高了聚類算法的適用性,，而且從圖1可以看出，E-MEDOIDS算法的運(yùn)行效率比K-MEDOIDS算法有一定的提高,。

　　3.2 參數(shù)E對(duì)算法的影響

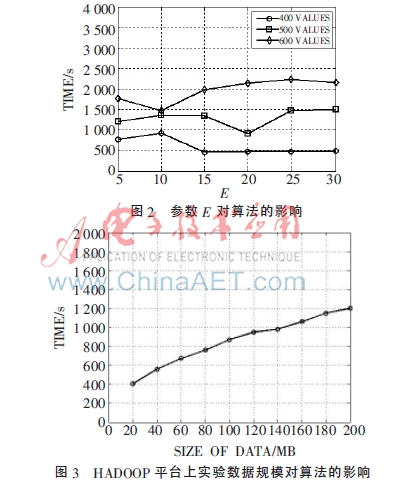
　　分別采用400,、500、600條目的數(shù)據(jù)集進(jìn)行實(shí)驗(yàn),，每次實(shí)驗(yàn)更改參數(shù)E的大小,，然后收集程序的運(yùn)行時(shí)間。圖2表明E-MEDOIDS參數(shù)E對(duì)算法的運(yùn)行效率整體影響不大,，但是當(dāng)參數(shù)E取得某一恰當(dāng)值（約等于固定詞條的長度）時(shí),，程序運(yùn)行時(shí)間取得最小值。因此,，正確設(shè)置參數(shù)E,，可以提高算法的效率。

　　3.3 HADOOP平臺(tái)上數(shù)據(jù)集規(guī)模對(duì)算法的影響

　　為了驗(yàn)證在大數(shù)據(jù)環(huán)境下算法的并行性,，在HADOOP平臺(tái)上使用大小不等的10組數(shù)據(jù)進(jìn)行實(shí)驗(yàn),。實(shí)驗(yàn)數(shù)據(jù)集由不同數(shù)量的單節(jié)點(diǎn)實(shí)驗(yàn)數(shù)據(jù)組成，生成的實(shí)驗(yàn)數(shù)據(jù)文件大小從20 MB~200 MB不等,。HADOOP實(shí)驗(yàn)平臺(tái)運(yùn)行20個(gè)MAP-REDUCE任務(wù),，實(shí)驗(yàn)結(jié)果如圖3所示。

　　由圖3可以看出,，隨著數(shù)據(jù)量增加,，HADOOP任務(wù)運(yùn)行時(shí)間也平緩增加。當(dāng)數(shù)據(jù)量較小時(shí),，算法運(yùn)行時(shí)間增長較快,；當(dāng)數(shù)據(jù)量較大時(shí)，運(yùn)行時(shí)間增長比較緩慢,。這是因?yàn)楫?dāng)數(shù)據(jù)量較大時(shí)才能發(fā)揮HADOOP平臺(tái)下算法并行運(yùn)算的優(yōu)勢，因此算法具有良好的并行性,。所以本文提出的基于MAP-REDUCE的聚類算法可以有效解決大數(shù)據(jù)環(huán)境下數(shù)據(jù)不一致性問題,。

4 結(jié)束語

　　大數(shù)據(jù)環(huán)境中，提高數(shù)據(jù)質(zhì)量也將成為數(shù)據(jù)價(jià)值再創(chuàng)造的關(guān)鍵之一,。當(dāng)分布在不同節(jié)點(diǎn)上的數(shù)據(jù)集成時(shí),，很容易引起數(shù)據(jù)不一致問題，嚴(yán)重影響數(shù)據(jù)質(zhì)量,。本文提出了基于MAP-REDUCE的聚類算法解決大數(shù)據(jù)環(huán)境下的數(shù)據(jù)不一致問題,。通過改進(jìn)K-MEDOIDS算法提出E-MEDOIDS算法，使聚類算法在處理數(shù)據(jù)不一致問題上適用性更強(qiáng),。又提出了EW-MEDOIDS算法,，引入節(jié)點(diǎn)的權(quán)重值對(duì)聚類算法進(jìn)行干預(yù),，進(jìn)一步提高聚類算法的精確性。而算法采用MAP-REDUCE框架實(shí)現(xiàn),，有效增強(qiáng)了聚類算法的并行性,，可高效解決大數(shù)據(jù)環(huán)境下的數(shù)據(jù)不一致問題。

　　目前,，EW-MEDOIDS算法的權(quán)重值是通過人工設(shè)定的,。當(dāng)數(shù)據(jù)節(jié)點(diǎn)量很大時(shí)，人工設(shè)置的方法將不適用,。未來可以在自動(dòng)設(shè)置權(quán)重值方面開展工作,，盡量減少不必要的人工操作。

參考文獻(xiàn)

　　[1] AEBI D,， PERROCHON L. Towards improving data quality[C]. CiSMOD,， 1993： 273-281.

　　[2] FAN W， GEERTS F. Foundations of data quality management[J]. Synthesis Lectures on Data Management,， 2012,，4（5）：1-217.

　　[3] RAHM E， DO H H. Data cleaning： problems and current approaches[J]. IEEE Data Eng. Bull.,， 2000,，23（4）：3-13.

　　[4] SHAHAMATNIA E， DOROTOVI I,， MORA A,， et al. Data inconsistency in sunspot detection[C]. Intelligent Systems′ 2014， Springer International Publishing,， 2015：567-577.

　　[5] DANILOWICZ C,， NGUYEN N T. Consensus methods for solving inconsistency of replicated data in distributed systems[J]. Distributed and Parallel Databases， 2003,，14（1）： 53-69.

　　[6] 孟小峰,，慈祥.大數(shù)據(jù)管理：概念，技術(shù)與挑戰(zhàn)[J].計(jì)算機(jī)研究與發(fā)展,，2013,，50（1）：146-169.

　　[7] KUMAR V V， DINESH K. Job scheduling using fuzzy neural network algorithm in cloud environment[J]. Bonfring International Journal of Man Machine Interface,， 2012,，2（1）：1-6.

　　[8] TEWARI N C， KODUVELY H M,， GUHA S,， et al. MapReduce implementation of variational bayesian probabilistic matrix factorization algorithm[C]. Big Data， 2013 IEEE International Conference on. IEEE,， 2013：145-152.