摘  要： 針對(duì)固定步長(zhǎng)比較法的跟蹤速度和精度不夠理想的特點(diǎn)，提出一種新的變步長(zhǎng)擾動(dòng)觀測(cè)法來跟蹤光伏電池的最大功率點(diǎn),。依據(jù)光伏電池的P-U曲線特性,，在最大功率點(diǎn)兩側(cè)采用不同的變步長(zhǎng)控制策略。在左側(cè),，采用較大的步長(zhǎng)選擇策略,。在右側(cè)，采用較小的步長(zhǎng)選擇策略,。同時(shí)給出步長(zhǎng)的選擇方法,。在MATLAB/Simulink環(huán)境下，搭建光伏電池最大功率點(diǎn)模型并進(jìn)行仿真,。仿真結(jié)果表明,，該算法可以顯著提高最大功率的跟蹤速度與精度,，有效抑制在最大功率點(diǎn)處的振蕩現(xiàn)象。

　　關(guān)鍵詞： 光伏電池特性,；最大功率點(diǎn)跟蹤,；變步長(zhǎng)；速度/精度

0 引言

　　太陽(yáng)能作為清潔可再生能源,，分布廣泛,，應(yīng)用前景好。當(dāng)今,，光伏發(fā)電系統(tǒng)已得到了廣泛的應(yīng)用,。在光伏發(fā)電系統(tǒng)中，光伏電池的運(yùn)行受到外部環(huán)境的影響,。光伏電池的運(yùn)行特性表明,，其最大輸出功率與光照強(qiáng)度、溫度等因素有關(guān),，且具有非線性特性,。因此，為了讓光伏電池工作在最佳狀態(tài),，必須使用可靠的控制算法對(duì)光伏電池的最大輸出功率進(jìn)行跟蹤控制,，以保證光伏電池始終能夠輸出最大功率，從而提高光伏電池的工作效率,。這一跟蹤過程稱為最大功率跟蹤（Maximum Power Point Tracking,，MPPT）。

　　常用的MPPT算法主要有恒定電壓法,、擾動(dòng)觀測(cè)法,、電導(dǎo)增量法以及智能MPPT算法。擾動(dòng)觀測(cè)法具有結(jié)構(gòu)簡(jiǎn)單,、被測(cè)量少,、控制簡(jiǎn)單、易于實(shí)現(xiàn)等優(yōu)點(diǎn),，應(yīng)用較廣,，但其存在振蕩及誤判問題，使系統(tǒng)很難準(zhǔn)確地跟蹤到最大功率點(diǎn),。

　　參考文獻(xiàn)[1]給出一種變步長(zhǎng)控制策略,，分析了P-U曲線的特性區(qū)間，在最大功率點(diǎn)附近采用小步長(zhǎng)擾動(dòng)觀測(cè)法,，在最大功率點(diǎn)兩側(cè)采用大步長(zhǎng)擾動(dòng)觀測(cè)法,。但是該文獻(xiàn)沒有給出大、小步長(zhǎng)的選取方法,。該策略沒有注意到P-U特性曲線在最大功率點(diǎn)兩側(cè)的變化率不同,，沒有給出步長(zhǎng)選擇算法,。

　　參考文獻(xiàn)[2]分析了|dP/dU|曲線在最大功率點(diǎn)（MPP）兩側(cè)的變化差異，提出了一種以P-U曲線切線角的正弦值為步長(zhǎng)參數(shù)的變步長(zhǎng)控制策略,。這種步長(zhǎng)選取方法能夠使得在最大功率點(diǎn)附近步長(zhǎng)變化更為平滑,、減小震蕩。但在遠(yuǎn)離最大功率點(diǎn)時(shí),，由于正弦函數(shù)值較小,，在一定的切線角度內(nèi)難以很好地區(qū)分步長(zhǎng)大小，進(jìn)而影響了跟蹤速度,。此方法還是沒有將最大功率點(diǎn)兩側(cè)的P-U曲線分開對(duì)待,，沒有分別采用不同的步長(zhǎng)選擇方法。

　　參考文獻(xiàn)[3]提出了一種變步長(zhǎng)MPPT算法,，其設(shè)定了三種不同的步長(zhǎng),，并根據(jù)功率變化的大小來選擇步長(zhǎng)。但是步長(zhǎng)還是固定的,，系統(tǒng)在最大功率點(diǎn)處的振蕩依然較大,。

　　綜上所述，以擾動(dòng)觀測(cè)法為基礎(chǔ),，依據(jù)P-U曲線特性,，在最大功率點(diǎn)兩側(cè)采用不同的步長(zhǎng)選擇方法，提出一種新型變步長(zhǎng)擾動(dòng)觀察法的MPPT算法,。不同的步長(zhǎng)選擇方法能夠優(yōu)化跟蹤速度與精度,，同時(shí)能夠減小在穩(wěn)態(tài)時(shí)的誤差。本文在對(duì)新的步長(zhǎng)選擇方法進(jìn)行分析后,，利用MATLAB/Simulink環(huán)境,，對(duì)光伏電池仿真研究。仿真實(shí)驗(yàn)中應(yīng)用本文所提的方法進(jìn)行MPPT控制,，實(shí)現(xiàn)了對(duì)最大功率點(diǎn)的跟蹤控制,，驗(yàn)證了該方法的高效性。

1 光伏電池模型及其特性分析

　　1.1 光伏電池?cái)?shù)學(xué)模型[4-6]

　　光伏電池的等效電路如圖1所示,。

　　圖1中Isc為光伏電池發(fā)出的電流,，IVD為二極管飽和電流。RL為光伏電池負(fù)載,，IL為負(fù)載電流,，負(fù)載電壓為UL,。

　　由圖1可得光伏電池的輸出特性方程為：

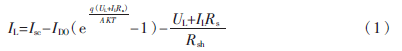
　　式中,，q為電荷量（1.6×10-19 C）；A為二極管因子,；K為玻爾茲曼常數(shù)（1.38×10-23 J/K）,；T為開氏溫度,；IL為光伏電池輸出電流；Isc為光伏電池短路電流,；IDO為光伏電池在無光照時(shí)的飽和電流,。

　　理想光伏電池其等效串聯(lián)電阻Rs較小，并聯(lián)電阻Rsh較大,。因此,，在理想模型下可以忽略Rs、Rsh的影響,。光伏電池的輸出特性可以表示為：

　　標(biāo)準(zhǔn)測(cè)試條件下,，光伏電池輸出特性的工程計(jì)算方法為：

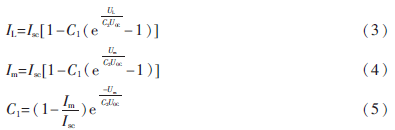
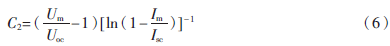
　　其中，Um,、Im為最大功率點(diǎn)輸出電壓,、電流；Uoc,、Isc為光伏電池的開路電壓,、短路電流。式（3）適用于標(biāo)準(zhǔn)照度Sref=1 000 W/m2,、標(biāo)準(zhǔn)溫度Tref=25 ℃時(shí)的光伏電池模型,。當(dāng)照度、溫度變化時(shí)就不再適用了,。所以,，工程上采用如下方法來修正Um、Im,、Uoc,、Isc。

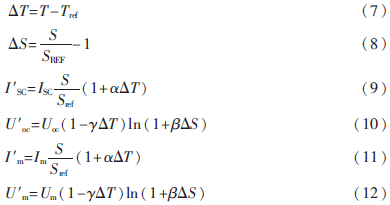
　　以上公式中系數(shù)α,、β,、γ的典型值為α=0.002 5，β=0.5,，γ=0.002 88,。依據(jù)以上數(shù)學(xué)模型，在MATLAB/Simulink環(huán)境下建立光伏電池的仿真模型,，并對(duì)電池的輸出電壓電流,、功率電壓等特性進(jìn)行分析研究。

　　1.2 光伏電池輸出特性分析

　　對(duì)光伏電池模型的分析可以發(fā)現(xiàn),，光照強(qiáng)度,、工作溫度和負(fù)載阻抗是影響光伏電池輸出功率的主要參數(shù)。光照強(qiáng)度主要影響光伏電池的短路電路，工作溫度主要影響光伏電池的開路電壓,。

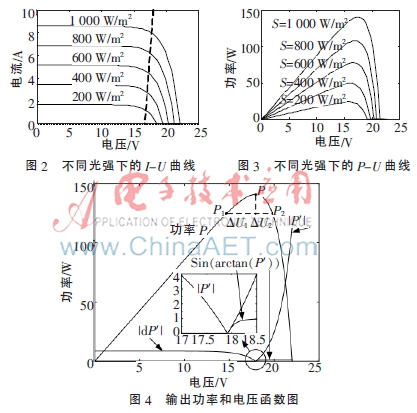
　　圖2為光伏電池的輸出電壓與電流關(guān)系曲線,，可以看出電壓與電流不具線性關(guān)系。從圖3的P-U特性曲線可以看出,，在最大功率點(diǎn)兩側(cè),，左側(cè)P-U曲線的變化較右側(cè)平緩。距離最大功率點(diǎn)相同距離處,，左側(cè)的|dP/dU|,，即|P′|值小于右側(cè)。由圖4中的|P′|曲線可以看出,，右側(cè)|dP/dU|的變化遠(yuǎn)大于左側(cè),。

2 擾動(dòng)觀測(cè)法原理

　　擾動(dòng)觀測(cè)法是目前實(shí)現(xiàn)MPPT最常用的自尋優(yōu)方法之一。擾動(dòng)觀測(cè)法的基本原理是：給光伏電池的輸出電壓施加一定量的定向擾動(dòng),，然后比較擾動(dòng)前后光伏電池輸出功率的變化,。若變化為正，輸出功率增加,，則保持原擾動(dòng)方向繼續(xù)擾動(dòng),，否則向反方向擾動(dòng)。在圖4中,，點(diǎn)P為最大功率點(diǎn),，P1處在左側(cè)，P2處在右側(cè),。要達(dá)到最大功率點(diǎn),，在P1要增大光伏電池輸出電壓ΔU1，在P2處要減小輸出電壓ΔU2,?？梢钥闯鲭妷焊淖兊拇笮〔煌处1>ΔU2,。且距離最大功率點(diǎn)越遠(yuǎn),，ΔU1與ΔU2差異越大。

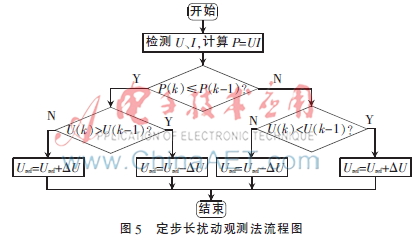
　　由于擾動(dòng)的存在,，擾動(dòng)觀測(cè)法很難消除在最大功率點(diǎn)處的來回振蕩現(xiàn)象,。同時(shí)，擾動(dòng)步長(zhǎng)的大小將直接影響最大功率跟蹤的速度與精度,。圖5為定步長(zhǎng)擾動(dòng)觀測(cè)法控制流程圖,。

3 改進(jìn)型變步長(zhǎng)擾動(dòng)觀測(cè)法

　　在定步長(zhǎng)擾動(dòng)觀測(cè)法中，為加快系統(tǒng)的跟蹤速度,，可適當(dāng)增大擾動(dòng)步長(zhǎng),。但是,，較大的擾動(dòng)步長(zhǎng)會(huì)加強(qiáng)光伏電池在最大功率點(diǎn)附近的振蕩。較小的擾動(dòng)步長(zhǎng)可以減小振蕩,，而系統(tǒng)的跟蹤速度會(huì)相應(yīng)下降。所以,，為解決速度與精度的矛盾,，出現(xiàn)了變步長(zhǎng)擾動(dòng)觀測(cè)法。傳統(tǒng)的變步長(zhǎng)擾動(dòng)觀測(cè)法有最優(yōu)梯度法,、逐步逼近法等,。由于在最大功率點(diǎn)右側(cè)，功率對(duì)電壓的導(dǎo)數(shù)P′值過大,，已經(jīng)不適合做步長(zhǎng)選擇參數(shù),。所以，基于最優(yōu)梯度法的變步長(zhǎng)擾動(dòng)觀測(cè)法由于采用統(tǒng)一的步長(zhǎng)選擇公式,，不能較好地適應(yīng)P-U曲線的變化,。

　　本文提出在最大功率點(diǎn)左側(cè)采用功率對(duì)電壓的導(dǎo)數(shù)作為步長(zhǎng)選擇參數(shù)，在最大功率點(diǎn)右側(cè)采用P-U曲線的切線角的正弦值作為步長(zhǎng)選擇參數(shù),。步長(zhǎng)選擇是變化的,，且步長(zhǎng)在接近最大功率點(diǎn)處具有收斂性，能夠很好地抑制在最大功率點(diǎn)附近的振蕩現(xiàn)象,。圖4中的小圖顯示了在最大功率點(diǎn)兩側(cè)步長(zhǎng)選擇參數(shù)的變化情況,。易得出在最大功率點(diǎn)處，基于P′與sin（arctan（|P′|））的兩種步長(zhǎng)參數(shù)都收斂到零,。

　　最大功率點(diǎn)左側(cè)步長(zhǎng)參數(shù)K1：

　　K1=P′=dP/dU=（P（k）-P（k-1））/（U（k）-U（k-1））（13）

　　最大功率點(diǎn)右側(cè)步長(zhǎng)參數(shù)K2：

　　K2=sin（arctan（|P′|））（14）

　　從式（13）,、式（14）可得，在最大功率點(diǎn)處,，P′=0,，P-U曲線的切線角為零。在從兩側(cè)向最大功率點(diǎn)接近的過程中,，K1,、K2都趨向零，進(jìn)而步長(zhǎng)趨向于零,。步長(zhǎng)在最大功率點(diǎn)附近具有收斂性,，所以步長(zhǎng)可以較小，進(jìn)而抑制振蕩,。圖6為改進(jìn)型變步長(zhǎng)擾動(dòng)觀測(cè)法流程圖,。

4 MATLAB/Simulink建模仿真研究

　　為驗(yàn)證所提出的改進(jìn)型變步長(zhǎng)擾動(dòng)觀測(cè)法的有效性，利用MATLAB/Simulink建立光伏發(fā)電系統(tǒng)仿真模型,，如圖7所示,。模擬光伏電池在環(huán)境溫度為25℃,，光照強(qiáng)度為600 W/m2、1 000 W/m2,、400 W/m2時(shí)的運(yùn)行情況,。光伏電池的開路電壓為22 V、短路電流為8.58 A,，最大功率點(diǎn)的電壓為17.7 V,、電流為7.94 A。通過Simulink的S函數(shù)編寫MPPT算法,，完成對(duì)光伏電池最大功率點(diǎn)的跟蹤控制,。

　　圖8中的小圖為局部放大圖?？梢钥闯霰疚乃崴惴黠@優(yōu)于傳統(tǒng)算法,。在開機(jī)跟蹤速度上，改進(jìn)型算法在不到0.001 s的時(shí)間內(nèi)即達(dá)到穩(wěn)定輸出,，而傳統(tǒng)算法約     0.001 5 s,。在跟蹤精度上，改進(jìn)型算法在最大功率點(diǎn)處無明顯振蕩,，而傳統(tǒng)算法振蕩較明顯,。在外部光照強(qiáng)度改變時(shí)，改進(jìn)型算法比傳統(tǒng)算法振蕩較小,。以上仿真結(jié)果表明,，改進(jìn)型算法的步長(zhǎng)參數(shù)要優(yōu)于傳統(tǒng)算法。

5 結(jié)論

　　本文首先分析了光伏電池的特性及數(shù)學(xué)模型,。在研究P-U特性曲線的基礎(chǔ)上,，分析影響最大功率點(diǎn)跟蹤速度與精度的問題。針對(duì)P-U曲線在最大功率點(diǎn)兩側(cè)變化的差異,，提出了改進(jìn)型變步長(zhǎng)擾動(dòng)觀測(cè)法,。通過MATLAB/Simulink環(huán)境搭建仿真模型，由S函數(shù)實(shí)現(xiàn)算法,，進(jìn)行仿真實(shí)驗(yàn),。仿真結(jié)果表明，本文所提的算法相比于定步長(zhǎng)算法具有跟蹤速度快,、精度高的特點(diǎn),。光伏電池在日照強(qiáng)度變化時(shí)依然能夠較快速穩(wěn)定地輸出最大功率。

參考文獻(xiàn)

　　[1] 張超.光伏發(fā)電系統(tǒng)變步長(zhǎng)MPPT控制策略研究[J].電力電子技術(shù),，2009,，43（10）：47-49.

　　[2] 王亞楠.一種新型變步長(zhǎng)光伏最大功率點(diǎn)跟蹤控制策略[J].電氣傳動(dòng)，2015,，45（1）：54-57.

　　[3] 朱銘煉,，李臣松.一種應(yīng)用于光伏系統(tǒng)的變步長(zhǎng)擾動(dòng)觀察法[J].電力電子技術(shù),，2010，44（1）：20-22.

　　[4] 張興,，曹仁賢.太陽(yáng)能光伏并網(wǎng)發(fā)電及其逆變控制[M].北京：機(jī)械工業(yè)出版社,，2011.

　　[5] MESSENGER R A， VENTRE J. Photovoltaic systems engineering（2nd ed）[M]. Boca Raton： CRC Press LLC,， 2004.

　　[6] 王長(zhǎng)貴,，王斯成.太陽(yáng)能光伏發(fā)電實(shí)用技術(shù)[M].北京：化學(xué)工業(yè)出版社，2005.