摘 要： 在傳統(tǒng)加權(quán)輪詢調(diào)度算法和嚴(yán)格優(yōu)先級調(diào)度算法的基礎(chǔ)上,，加入令牌桶機制，實現(xiàn)了一種改進算法,。在多業(yè)務(wù)并存網(wǎng)絡(luò)中,，該算法能夠?qū)Σ煌燃壍臉I(yè)務(wù)實現(xiàn)不同的QoS（服務(wù)質(zhì)量），同時,，在業(yè)務(wù)流量發(fā)生變化時,，能夠動態(tài)調(diào)整相應(yīng)業(yè)務(wù)的帶寬，且不會對高優(yōu)先級隊列造成影響,。仿真實驗表明,，該算法可以在一定范圍內(nèi)適應(yīng)網(wǎng)絡(luò)的變化，有效緩解了突發(fā)流量所造成的報文丟包問題,，大大提高了網(wǎng)絡(luò)性能,。
關(guān)鍵詞： 多業(yè)務(wù)網(wǎng)絡(luò)；QoS；動態(tài)調(diào)整,；丟包
0 引言
隨著科技的飛速發(fā)展,，網(wǎng)絡(luò)中的業(yè)務(wù)量也呈爆炸式的增長，而且不同的業(yè)務(wù)在時延,、丟包等性能方面也有著不同程度的要求,。但網(wǎng)絡(luò)資源總是有限的，在網(wǎng)絡(luò)總帶寬固定的情況下,，如果某類業(yè)務(wù)占用的帶寬越多,，那么其他業(yè)務(wù)能使用的帶寬就越少，可能會影響其他業(yè)務(wù)的使用,?；诖耍瑢＜覀兲岢隽薗oS的概念,，針對各種應(yīng)用的不同需求,，來對網(wǎng)絡(luò)資源進行合理的規(guī)劃和分配，從而使網(wǎng)絡(luò)資源得到高效利用,。
隊列調(diào)度機制作為QoS技術(shù)的核心機制之一，一直以來就是研究的熱點,。所謂隊列調(diào)度就是在網(wǎng)絡(luò)中傳送業(yè)務(wù)時,，如何從多個數(shù)據(jù)包隊列中選擇一個隊列轉(zhuǎn)發(fā)[1]。一個好的隊列調(diào)度算法可以大大提高網(wǎng)絡(luò)的性能,，這在帶寬資源擴展速度遠遠落后于網(wǎng)絡(luò)中消息增加速度的今天,，重要性不言而喻。
目前,，已有很多種隊列調(diào)度算法被提出,，如嚴(yán)格優(yōu)先級隊列調(diào)度（Strict Priority，SP）算法,、加權(quán)輪詢調(diào)度（Weighted Round Robin,，WRR）算法、加權(quán)差額輪詢調(diào)度（Weighted Deficit Round Robin,，WDRR）算法,、加權(quán)公平調(diào)度（Weighted Fair Queuing，WFQ）算法等[2-4],，但面對千變?nèi)f化的網(wǎng)絡(luò)環(huán)境,，這些算法總是存在著這樣或那樣的缺陷。本文在研究了傳統(tǒng)的各種隊列調(diào)度算法之后,，在WRR算法的基礎(chǔ)上加以改進,，大大提高了算法的性能，且能在一定范圍內(nèi)適應(yīng)網(wǎng)絡(luò)中流量的變化,。
1 幾種典型的隊列調(diào)度算法
1.1 SP算法
SP算法是針對關(guān)鍵業(yè)務(wù)應(yīng)用設(shè)計的,。SP算法嚴(yán)格按照優(yōu)先級從高到低的順序調(diào)度隊列,，當(dāng)高優(yōu)先級報文中存在報文時，低優(yōu)先級隊列得不到調(diào)度的機會,。這就導(dǎo)致SP算法雖然可以保證高優(yōu)先級隊列的服務(wù)質(zhì)量（Quality of Service,，QoS），但是當(dāng)高優(yōu)先級隊列中始終有報文存在時,，低優(yōu)先級隊列中的報文得不到調(diào)度,，造成低優(yōu)先級隊列“餓死”現(xiàn)象。
1.2 WRR算法
WRR算法解決了SP算法中低優(yōu)先級隊列“餓死”的問題,。在WRR調(diào)度算法中根據(jù)隊列的權(quán)值來決定轉(zhuǎn)發(fā)報文的數(shù)量,。首先設(shè)置一個變量weight記錄隊列的權(quán)值，在進行隊列調(diào)度時,，首先判斷weight值是否大于0以及隊列是否非空,，若weigdt大于0且隊列非空，則從該隊列中轉(zhuǎn)發(fā)一個分組,，并將weight減1,，繼續(xù)進行條件判斷，直到weight值等于0或隊列為空,，轉(zhuǎn)到下一個隊列開始調(diào)度,，當(dāng)所有隊列都輪詢一遍后，將每個隊列的weight值恢復(fù)為初始值,，然后從第一個隊列開始,，再次遍歷，不停地重復(fù)以上步驟,。
1.3 WDRR算法
WRR調(diào)度雖然解決了SP調(diào)度中的低優(yōu)先級隊列“餓死”問題,，但由于算法以分組為單位進行隊列調(diào)度，當(dāng)隊列中分組長度不同時,，就會導(dǎo)致調(diào)度的公平性問題,。由此，提出了以字節(jié)為單位來進行調(diào)度的WDRR調(diào)度,。WDRR算法中首先要設(shè)置一個粒度值表示每個權(quán)值所代表的字節(jié)數(shù),，并設(shè)置一個變量DC[i]表示第i個隊列在一次輪詢中可以調(diào)度的字節(jié)數(shù)，初始化為0,。每輪調(diào)度隊列之前計算隊列權(quán)值與粒度的乘積加上DC[i]的初值,，作為本輪調(diào)度可以轉(zhuǎn)發(fā)的最大字節(jié)數(shù)，隊列調(diào)度過程如下：
?。?）DC[i]=DC[i]+粒度*權(quán)值,；
（2）若隊列為空，則只需將DC[i]置0,，轉(zhuǎn)到下一隊列開始調(diào)度,；
（3）若隊列不為空,，則比較DC[i]與接下來要調(diào)度的分組長度length的大小,，若DC[i]>=length，則轉(zhuǎn)發(fā)該分組,，更新DC[i]的值（DC[i]=DC[i]-length）,，并轉(zhuǎn)向（2），否則轉(zhuǎn)到下一個隊列繼續(xù)調(diào)度,；
?。?）若一輪調(diào)度完成，則轉(zhuǎn)到第一個隊列,，轉(zhuǎn)到（2）,，繼續(xù)調(diào)度。
DWRR調(diào)度雖然解決了WRR調(diào)度中的公平性問題,，但仍然存在如下一系列的缺點[5-6]：
?。?）不能體現(xiàn)高優(yōu)先級隊列的絕對優(yōu)先級地位。
?。?）分組時延得不到保證,，當(dāng)某一分組錯過了本次調(diào)度時，它將不得不等待一個輪詢周期的時間,，尤其是當(dāng)這種情況出現(xiàn)在高優(yōu)先級隊列時，會造成嚴(yán)重后果,。
?。?）各隊列分配到的權(quán)值是固定的，當(dāng)網(wǎng)絡(luò)情況發(fā)生變化時,，不能很好地適應(yīng),，例如，高優(yōu)先級報文突然增多,，但由于分配的帶寬已經(jīng)固定了,，多余的報文將得不到轉(zhuǎn)發(fā)，只能丟棄,。
2 改進算法描述
本文針對以上算法存在的缺點,，提出一種改進的隊列調(diào)度算法，經(jīng)驗證,，改進算法很好地解決了以上問題,。其基本流程如下：
（1）報文入普通8隊列。報文根據(jù)dscp值映射出本地優(yōu)先級,，根據(jù)本地優(yōu)先級進入相應(yīng)的8隊列,。
（2）對隊列進行分組,。將QoS需求近似的隊列分在同一組,，每一組以組中優(yōu)先級最低隊列的優(yōu)先級作為本組中所有隊列的優(yōu)先級（避免優(yōu)先級重復(fù)）。為了保證高優(yōu)先級隊列的絕對優(yōu)先地位,，不同組之間的隊列按照SP算法進行調(diào)度,，保證高優(yōu)先級隊列優(yōu)先轉(zhuǎn)發(fā)。同一組內(nèi)的各隊列之間進行DWRR調(diào)度,，保證QoS需求近似隊列的相對公平性,。
（3）從8隊列（QueueLoop[8]）映射到64隊列（FlowLoop[64]）,。本設(shè)計提供一套模板,，該模板包含64個隊列，分8種優(yōu)先級,，每個隊列都設(shè)定好了對應(yīng)優(yōu)先級值（priority）,。首先從QueueLoop[1]開始，以此與FlowLoop進行匹配,，若優(yōu)先級相同且FlowLoop還未被其他隊列占用,，則匹配成功，進行下一條QueueLoop的匹配工作,，否則繼續(xù)匹配,，直到匹配成功為止，流程如圖1,。
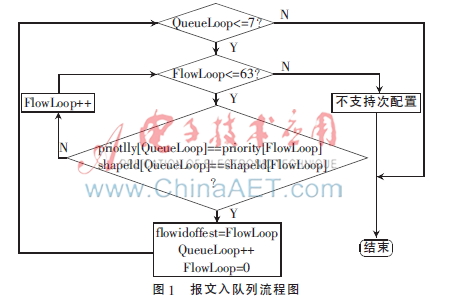
?。?）隊列調(diào)度。如上所述,，分組內(nèi)進行DWRR調(diào)度,，分組間進行SP調(diào)度。為了使低優(yōu)先級隊列不被“餓死”,，本算法引入了令牌桶機制對隊列和整個分組進行限速,，對每個隊列的超帶寬流量進行降級處理，將優(yōu)先級降為最低,，并加入優(yōu)先級最低的分組與組中原有隊列按權(quán)值共享剩余帶寬,。這樣當(dāng)隊列出現(xiàn)突發(fā)流量時，可以有效減小突發(fā)報文的丟包率,，并且在低優(yōu)先級隊列空閑時可以自動占用剩余帶寬,，避免浪費,，算法調(diào)度的框架如圖2所示。
3 實驗及結(jié)果分析
本文在實體路由器上進行測試,，實驗組網(wǎng)如圖3所示,。
用打流儀構(gòu)建8條優(yōu)先級各不相同的流，其中6,、7隊列為高優(yōu)先級隊列,，要求快速轉(zhuǎn)發(fā)（EF），2~5隊列為中優(yōu)先級隊列,，要求保障轉(zhuǎn)發(fā)（AF）,，0、1隊列為低優(yōu)先級隊列,，要求盡力而為地轉(zhuǎn)發(fā)（BE）[7],。發(fā)送端g2/1/5流量的發(fā)送速率除5隊列外，都固定為100 MB/s（每個優(yōu)先級報文為100 MB/s）,，路由器出端口g2/1/6限速為700 MB/s,。在上圖構(gòu)建的通路中，分別執(zhí)行WRR算法和本文改進的算法,，統(tǒng)計在不同算法下各隊列的調(diào)度情況,。
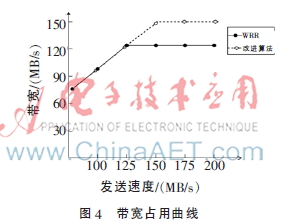
首先驗證各算法對網(wǎng)絡(luò)的適應(yīng)情況，將隊列5的報文發(fā)送速率逐步從100 MB/s增加到200 MB/s,，比較各隊列占用帶寬的情況,。對WRR算法，設(shè)置8隊列的權(quán)值分別為3,、3,、2、2,、1,、1、1,、1。對本文改進的算法,，在以上所設(shè)基礎(chǔ)上,，將8條流量分為三組，第一組包含隊列0和隊列1,，第二組為隊列2到5,，剩下的隊列分到第三組，同時對第二組限速350 MB/s,，結(jié)果如圖4所示,?？梢姡?dāng)流量增加時,，WRR算法對網(wǎng)絡(luò)變化缺乏調(diào)控能力,，而改善算法對超帶寬的流量做了降級處理，在第一組中得以再次調(diào)度,，等于增加了權(quán)值,，分配到了更多帶寬，且不會對比其優(yōu)先級高的隊列造成影響,，也不會造成低優(yōu)先級隊列“餓死”,，改進的算法對流量調(diào)控起到了一定的作用。
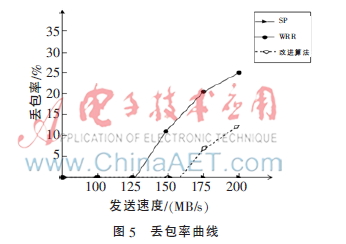
接下來驗證隊列的丟包情況,，在擁塞的網(wǎng)絡(luò)環(huán)境中必然會有丟包,。既然丟包是必然的，就要盡量保證優(yōu)先級高的隊列少丟包,。以下比較三種算法的丟包情況,。首先構(gòu)建這樣的網(wǎng)絡(luò)環(huán)境，在上文的條件基礎(chǔ)上將隊列5報文到達速率不停地增加,，觀察該隊列的丟包情況,。如圖5所示。改進算法的丟包率遠遠小于WRR算法的丟包率,，SP算法丟包率雖然低,，但是它是以更多低優(yōu)先級隊列“餓死”為代價的。
4 結(jié)論
本文在現(xiàn)有SP算法和WRR算法的基礎(chǔ)上作出改進,，主要是為了實現(xiàn)不同業(yè)務(wù)的不同服務(wù)質(zhì)量要求,，同時提高對網(wǎng)絡(luò)變化的自適應(yīng)性。仿真實驗證明,，當(dāng)某分組到達隊列的速率不斷加快時,，通過對超帶寬流量降級，使其更低優(yōu)先級分組得到再次調(diào)度的機會,，相當(dāng)于增加了該隊列的權(quán)值,，實現(xiàn)了帶寬資源的動態(tài)分配。同時,，算法還大大減小了網(wǎng)絡(luò)丟包率,。
參考文獻
[1] 林闖，單志廣,，任豐原.計算機網(wǎng)絡(luò)的服務(wù)質(zhì)量（QoS）[M].北京：清華大學(xué)出版社,，2004.
[2] 董民，沈慶國.輪詢類分組調(diào)度算法的研究[J].系統(tǒng)仿真學(xué)報,，2010,，22（11）：2593-2596.
[3] 熊李艷,，張勝輝.WRR算法在多類別實時數(shù)據(jù)流中的優(yōu)化[J].計算機科學(xué)與工程，2012,，34（7）：35-38.
[4] NIKOLOVA D,， BLONDIA C. Bonded deficit robin scheduling for multi-channel networks[J]. Computer Networks，2011,，55（15）,，3503-3516.
[5] Li Miaoyan，Song Bo. Design and implementation of a new queue scheduling scheme in DiffServ networks[C]. The 2nd IEEE International Conference on Advanced Computer ConTrol,， 2010：117-122.
[6] ZHANG Y,， HARRISON P G. Performance of a priority-weighted round robin mechanism for differentiated service networks[C]. International Conference on Computer Communications and Networks， 2007：1198-1203.
[7] 劉威,，楊宗凱.多服務(wù)級別帶寬公平分配算法的研究[J].計算機科學(xué),，2005，32（1）：37-40.