摘  要： 對(duì)比分析了最小半徑泊車算法和不等半徑泊車算法的基本原理，分析了汽車在低速情況下泊車入庫(kù)時(shí)的后輪軌跡特點(diǎn),。同時(shí)在MATLAB環(huán)境下對(duì)兩種算法進(jìn)行了仿真研究,，并且對(duì)仿真數(shù)據(jù)進(jìn)行了比較分析。結(jié)果表明,，不等半徑泊車算法對(duì)泊車起始位置要求相對(duì)較低,，更符合實(shí)際操作需求。

　　關(guān)鍵詞： 自動(dòng)泊車系統(tǒng),；泊車路徑規(guī)劃,；建模與仿真

0 引言

　　自動(dòng)泊車系統(tǒng)是一種智能汽車安全輔助系統(tǒng),，是一種全新的智能駕駛技術(shù),，它能夠使汽車駕駛員在復(fù)雜的城市環(huán)境內(nèi)快速便捷地完成泊車任務(wù),，降低了因泊車空間狹小或駕駛技術(shù)不熟練而引發(fā)交通事故的概率，對(duì)于當(dāng)前汽車工程領(lǐng)域的研發(fā)具有重要意義[1-2],。

　　近幾年,，國(guó)內(nèi)外很多學(xué)者對(duì)自動(dòng)泊車系統(tǒng)進(jìn)行了相關(guān)研究。法國(guó)國(guó)立計(jì)算機(jī)及自動(dòng)化研究院Paromtchik等人研究了泊車運(yùn)動(dòng)軌跡方面的工作[3],，臺(tái)灣成功大學(xué)Chao等人通過(guò)全景攝像頭獲取模型小車相對(duì)于車位之間的位置并生成可行的參考泊車路徑[3],，德國(guó)艾爾默斯公司（Elmos）宣布推出可用于驅(qū)動(dòng)超聲波傳感器的E524.02和E524.03數(shù)字超聲波倒車輔助系統(tǒng)系列芯片[4]，其中浙江大學(xué)開(kāi)展的相關(guān)研究是該領(lǐng)域的優(yōu)秀代表,。浙江大學(xué)周泓,、王文飛對(duì)實(shí)現(xiàn)自動(dòng)泊車系統(tǒng)涉及到的3個(gè)核心算法進(jìn)行了探索和研究[5]，根據(jù)泊車位空間信息,，通過(guò)泊車路徑算法計(jì)算出一條最簡(jiǎn)單泊車的行車路徑,，但是并沒(méi)有將該算法與不等半徑泊車算法進(jìn)行對(duì)比，沒(méi)有對(duì)泊車起始位置的誤差進(jìn)行數(shù)據(jù)分析,。本文針對(duì)泊車起始位置的選擇,，以泊車路徑規(guī)劃為依據(jù)，對(duì)比分析了最簡(jiǎn)單泊車算法和不等半徑泊車算法的基本原理,，通過(guò)仿真數(shù)據(jù)分析,，總結(jié)出兩種泊車算法對(duì)汽車起始位置的約束范圍。

1 模型建立與算法分析

　　1.1 運(yùn)動(dòng)學(xué)模型的建立

　　正常情況下,，汽車倒車過(guò)程可以認(rèn)為是低速保持不變的過(guò)程[6],，在這種情況下車輪不會(huì)發(fā)生側(cè)滑，可以認(rèn)為車后輪垂直方向速度為0,，其方程式為：

　　根據(jù)圖1車輛運(yùn)動(dòng)學(xué)模型[7]可知,，汽車前、后軸中心點(diǎn)位置關(guān)系有：

　　對(duì)式（2）進(jìn)行微分,，得到其速度關(guān)系表達(dá)式：

　　由此將式（5）代入式（4）,，即可求得車輛回轉(zhuǎn)圓角速度為：

　　將式（5）、（6）代入式（3）得到后軸線中心點(diǎn)在x,、y方向上的速度為：

　　然后將式（6）對(duì)時(shí)間積分,，最后代入式（7）后，再對(duì)時(shí)間微分,，即可得到后輪軸線中心點(diǎn)軌跡方程：

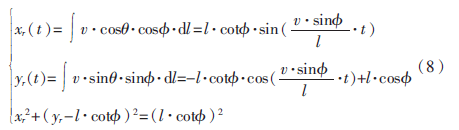
　　1.2 泊車算法分析

　　1.2.1 最簡(jiǎn)單泊車算法

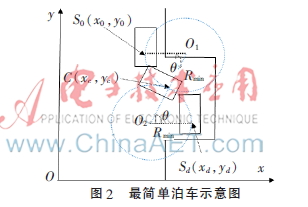
　　由圖2最簡(jiǎn)單泊車示意圖可知,，車輛泊車軌跡是由兩段相切的圓弧組合而成的S形曲線。最簡(jiǎn)單泊車過(guò)程中,，汽車始終以最小轉(zhuǎn)彎半徑運(yùn)動(dòng),。汽車首先往停車位方向?qū)⒎较虮P(pán)打死，從起始位置S0（x0,，y0）到達(dá)兩段圓弧的切點(diǎn)C,，然后再反方向打死方向盤(pán)直至到達(dá)目標(biāo)位置Sd（xd,，yd）。根據(jù)數(shù)學(xué)理論基礎(chǔ)可知,，車輪劃過(guò)的圓弧曲線長(zhǎng)度最短,，所需的停車位空間最小，汽車可以方便快速地完成泊車任務(wù),。

　　1.2.2 不等半徑泊車算法

　　由于最簡(jiǎn)單泊車算法對(duì)汽車起始位置要求較高,，當(dāng)車輛未能到達(dá)標(biāo)準(zhǔn)起始位置時(shí)，容易導(dǎo)致泊車過(guò)程失敗,。其失敗的主要原因在于汽車兩段泊車軌跡均以最小泊車半徑運(yùn)動(dòng),，起始位置可控范圍較小[8]。由圖3不等半徑泊車示意圖可知,，如果將第一段泊車軌跡改為不等半徑運(yùn)動(dòng),，那么對(duì)于汽車起始位置的要求會(huì)大大降低，整個(gè)泊車過(guò)程更加簡(jiǎn)單方便,。

2 仿真結(jié)果分析

　　本文根據(jù)運(yùn)動(dòng)學(xué)模型建立MATLAB仿真[9],，由汽車后輪軸中心點(diǎn)軌跡方程進(jìn)行仿真，其結(jié)果如圖4所示,。

　　由軌跡方程和圖4汽車后輪軌跡圖容易得知,，汽車車輪始終在做等半徑同心圓運(yùn)動(dòng)，車后輪軌跡與汽車軸距和車身轉(zhuǎn)向角有關(guān),，而與汽車行駛速度無(wú)關(guān),，由此可以得出，汽車泊車過(guò)程實(shí)際是汽車車輪反復(fù)畫(huà)圓弧的過(guò)程,?；谠摾碚摶A(chǔ)，下面對(duì)泊車過(guò)程軌跡進(jìn)行仿真分析,。

　　通過(guò)建立笛卡爾坐標(biāo)系,，對(duì)汽車車身各點(diǎn)坐標(biāo)進(jìn)行準(zhǔn)確的定位，從而對(duì)泊車過(guò)程中的泊車軌跡進(jìn)行仿真,，最簡(jiǎn)單泊車,、不等半徑泊車軌跡圖分別如圖5、圖6所示,。由仿真圖可知,，雖然不等半徑泊車算法的第一段泊車半徑明顯大于汽車最小轉(zhuǎn)彎半徑，而且汽車所需的停車位長(zhǎng)度也明顯增加,，但是其對(duì)于汽車起始位置的可控范圍明顯增大,。

　　不同的汽車駕駛員具有不同的駕駛習(xí)慣和駕駛技能，在實(shí)際操作中,，無(wú)法保證每一個(gè)駕駛員都能準(zhǔn)確到達(dá)標(biāo)準(zhǔn)的起始位置,。出于以上情況的考慮,，下面將從起始位置的變化范圍對(duì)兩種算法進(jìn)行仿真數(shù)據(jù)分析和比較。

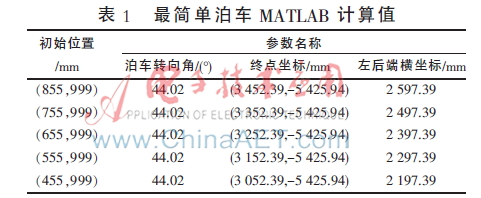
　　通過(guò)表1第1組數(shù)據(jù)的汽車后軸中心點(diǎn)坐標(biāo)易求得泊車空間右墻面頂點(diǎn)坐標(biāo)為（4 407.39,，-6 524.94），據(jù)數(shù)據(jù)統(tǒng)計(jì),，普通停車位的大小為2.2 m×7.5 m[10-11],，由此可確定最簡(jiǎn)單泊車算法的橫向坐標(biāo)變化范圍為2 207 mm~4 407 mm。同時(shí),，由圖7和表1第5組數(shù)據(jù)容易得到當(dāng)汽車起始位置為（455,，999）時(shí)，汽車左下端橫坐標(biāo)為  2 197.39,，小于最簡(jiǎn)單泊車橫坐標(biāo)變化范圍的最小值,，此時(shí)，汽車車身超出停車位空間,，最簡(jiǎn)單泊車方案失敗,。在這種情況下，汽車后軸中心點(diǎn)的橫向位置變化范圍不足400 mm,，這對(duì)于駕駛員對(duì)起始位置的控制有著很高的要求,，缺乏一定的靈活性。

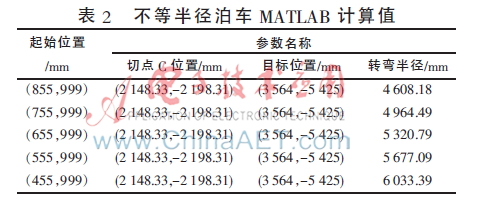
　　根據(jù)表2數(shù)據(jù)分析可知,，隨著汽車起始位置的改變,，第一段泊車半徑也逐漸增大，且大于汽車最小轉(zhuǎn)彎半徑,。另外,，由圖8和表2第5組數(shù)據(jù)可知，當(dāng)起始位置為（455,，999）時(shí),，第一段泊車半徑為6 888.39 mm，小車成功到達(dá)目標(biāo)位置,，順利完成泊車過(guò)程,，相比最簡(jiǎn)單泊車的橫向位置變化范圍，該算法更加靈活方便,。

　　對(duì)于有效的起始位置,，必須保證在泊車過(guò)程中不與周圍的障礙物發(fā)生碰撞。通過(guò)數(shù)學(xué)建模,，可以將這一問(wèn)題簡(jiǎn)化為兩個(gè)約束條件[5]：

　　其中,，LBo1為圓心O1到前方障礙物的距離，L為車寬,。

　　由此可以確定橫向位置的變化范圍：

　　確定了橫向位置的變化范圍,，再通過(guò)橫縱坐標(biāo)的幾何關(guān)系,，同理可以確定縱向位置的變化范圍。下面通過(guò)改變汽車起始位置和目標(biāo)位置的坐標(biāo),，由兩個(gè)約束條件計(jì)算出汽車起始橫向位置和縱向位置的變化范圍,，如表3所示。

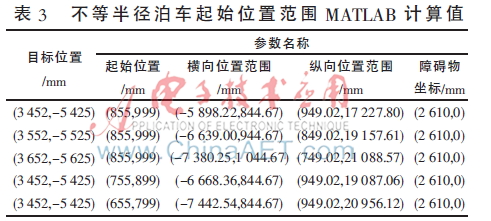
　　通過(guò)表3數(shù)據(jù)分析可知,，不同的起始位置和目標(biāo)位置所對(duì)應(yīng)的水平橫向位移不同,。不等半徑泊車算法使起始位置的選擇不再局限于一點(diǎn)上，更加符合實(shí)際的需要,，通過(guò)該算法使泊車過(guò)程更加方便快捷,。

3 結(jié)論

　　本文首先通過(guò)建立泊車過(guò)程的運(yùn)動(dòng)學(xué)模型，得到車輪運(yùn)動(dòng)軌跡表達(dá)式,，然后通過(guò)在MATLAB下的泊車軌跡仿真,，驗(yàn)證了最簡(jiǎn)單泊車和不等半徑泊車的可行性，并且將兩者進(jìn)行對(duì)比分析仿真,，得到不等半徑泊車算法對(duì)汽車起始位置的要求相比最簡(jiǎn)單泊車算法更加符合實(shí)際需求,，對(duì)于起始位置的選擇更加靈活方便。

參考文獻(xiàn)

　　[1] 祿盛,，黃顯杭,，蘇嶺，等.自動(dòng)泊車系統(tǒng)模型研究與實(shí)車驗(yàn)證[J].重慶郵電大學(xué)學(xué)報(bào)（自然科學(xué)版）,，2014,，26（4）：522-529.

　　[2] Ryu Young-woo， Oh Se-young,， Kim Sam-yong. Ro-bust automatic parking without odometry using en-hanced fuzzy logic controller[A]. IEEE International Conference on Fuzzy Systems,， Sheraton Vamcouver Wall Centre Hotel， Vancouver,， BC,， Conda， 2006.

　　[3] 樸昌浩,，祿盛,，張艷，等.自動(dòng)泊車系統(tǒng)設(shè)計(jì)[M].北京：科學(xué)出版社,，2014.

　　[4] 艾爾默斯公司.數(shù)字超聲波倒車輔助系統(tǒng)[J].微型機(jī)與應(yīng)用,，2013，32（10）：89.

　　[5] 周泓,，王文飛.自動(dòng)泊車系統(tǒng)中核心算法的研究[J].電路與系統(tǒng)學(xué)報(bào),，2012，17（3）：71-76.

　　[6] 楊妮娜，梁華為,，王少平.平行泊車的路徑規(guī)劃方法及其仿真研究[J].電子測(cè)量技術(shù),，2011，34（1）：42-45.

　　[7] 張偉東.基于預(yù)瞄點(diǎn)的自動(dòng)倒車設(shè)計(jì)和實(shí)現(xiàn)[J].輕工機(jī)械,，2011,，29（3）：96-100.

　　[8] 王道斌，梁華為,，楊妮娜,，等.兩種自主泊車路徑規(guī)劃方法的對(duì)比研究[J].電子測(cè)量技術(shù)，2011,，34（1）：27-31.

　　[9] 薛年喜.MATLAB在數(shù)字信號(hào)處理中的應(yīng)用[M].北京：清華大學(xué)出版社，2008.

　　[10] 羅奕樹(shù),，張?jiān)邶?，王日?自動(dòng)泊車小車轉(zhuǎn)彎參數(shù)及特征環(huán)境參數(shù)的確定[J].閩江學(xué)院學(xué)報(bào)，2011,，32（5）：46-50.

　　[11] Zhao Yanan,， EMMANUEL G． Collins Jr．. Robust automatic parallel parking in tight spaces via fuzzy logic[J].Robotics and Autonomous Systems， 2005（51）：111-127.