摘  要： 針對無線傳感器網(wǎng)絡(luò)定位技術(shù)中DV-Hop算法在最后階段計算待定位節(jié)點坐標(biāo)時定位精度低的問題,，提出了一種基于自適應(yīng)步長螢火蟲優(yōu)化算法的改進(jìn)DV-Hop算法（ASGSODV-Hop）,。該算法將DV-Hop算法在估算節(jié)點坐標(biāo)階段所使用的最小二乘法用ASGSO算法代替，采用ASGSO智能算法的自適應(yīng)迭代尋優(yōu)對DV-Hop算法定位求解的問題建立特定的適應(yīng)度函數(shù)并進(jìn)行多次迭代計算實現(xiàn)優(yōu)化,，最終使待定位節(jié)點坐標(biāo)與真實值更為接近,。仿真結(jié)果表明，該算法的平均定位誤差約為23.58%,；相比于傳統(tǒng)DV-Hop算法,，ASGSODV-Hop算法可在無需附加通信開銷的情況下使定位誤差降低約46.49%，提高了節(jié)點的定位精度,。

　　關(guān)鍵詞： 無線傳感器網(wǎng)絡(luò),；DV-Hop算法；ASGSO算法,；自適應(yīng)迭代,；定位精度

0 引言

　　無線傳感器網(wǎng)絡(luò)（Wireless Sensor Networks，WSNs）是一種集信息采集,、處理和傳輸于一身的智能網(wǎng)絡(luò)信息系統(tǒng)[1],，可在任何時間、地點和環(huán)境下獲取各種詳細(xì),、精確的目標(biāo)信息,，實現(xiàn)人與物理世界的通信和信息交互，節(jié)點定位技術(shù)為WSN的關(guān)鍵技術(shù),。目前與定位相關(guān)的算法可分為測距和非測距兩種,，測距定位算法通常有很高的精度，但需要較大的通信開銷和能耗；非測距定位算法是通過網(wǎng)絡(luò)連通性來實現(xiàn)定位,，無需附加的硬件支持,，是目前定位機(jī)制的研究重點。傳統(tǒng)的非測距定位算法有質(zhì)心算法[2],、DV-Hop算法[3-4],、近三角形內(nèi)點測試法（Approximate Point-in-triangulation Test，APIT）[5]等,。

　　DV-Hop算法采取距離向量—跳段機(jī)制,，由于其實現(xiàn)難度低，是一種常見的非測距定位算法,。目前很多學(xué)者提出了一些改進(jìn)算法以提高定位精度：文獻(xiàn)[6]采用改進(jìn)的加權(quán)最小二乘法得到待定位節(jié)點的坐標(biāo)以提高定位精度,，但通信量過大；文獻(xiàn)[7]采用蝙蝠算法（Bat Algorithm,，BA）對DV-Hop算法的定位結(jié)果進(jìn)行優(yōu)化,，但消耗了過多的資源；文獻(xiàn)[8]采用誤差跳距加權(quán)策略修正平均跳距,，并利用自適應(yīng)步長粒子群優(yōu)化（Self-adaptive Step Particle Swarm Optimization,，ASPSO）算法對DV-Hop算法的估計位置進(jìn)行優(yōu)化，精度有所提升,，但增加了計算量和通信開銷。本文采用自適應(yīng)步長螢火蟲優(yōu)化（Self-adaptive Step Glowworm Swarm Optimization,，ASGSO）算法[9]對估算位置進(jìn)行優(yōu)化,。仿真結(jié)果表明，在無需附加通信量和計算開銷的基礎(chǔ)上可減少定位誤差,，經(jīng)過優(yōu)化后算法的定位精度遠(yuǎn)大于DV-Hop算法的精度,。

1 DV-Hop算法

　　DV-Hop算法是由Rutgers大學(xué)的Dragons等人依據(jù)距離矢量路由和全球定位系統(tǒng)（Global Positioning System，GPS）提出的一種非測距定位算法,。其原理是采用距離矢量路由法得到待定位節(jié)點與信標(biāo)節(jié)點間的跳數(shù)最小值,，同時計算出平均跳距，以平均跳距與跳數(shù)最小值的乘積作為信標(biāo)節(jié)點和待定位節(jié)點的估算間距,，并通過極大似然估計法計算出待定位節(jié)點的坐標(biāo),。DV-Hop算法可大體分為以下3個階段：

　　（1）獲取待定位節(jié)點和信標(biāo)節(jié)點間的最小跳數(shù)

　　由信標(biāo)節(jié)點向相鄰節(jié)點傳送自身信標(biāo)信息,，包含信標(biāo)節(jié)點的標(biāo)識符,、位置及跳數(shù)值，將跳數(shù)初始化為0,。記錄并更新所接收信標(biāo)信息的鄰居節(jié)點到每一信標(biāo)節(jié)點的最小跳數(shù)并忽略較大的信標(biāo)信息,，跳數(shù)的值增加1，繼續(xù)向其鄰居節(jié)點廣播自身信息。當(dāng)網(wǎng)路中的全部待定位節(jié)點均記下距每一信標(biāo)節(jié)點的跳數(shù)最小值后此階段終止,。

　?。?）待定位節(jié)點與信標(biāo)節(jié)點間距離的估計

　　經(jīng)過第一階段，信標(biāo)節(jié)點i得到與其余信標(biāo)節(jié)點之間的位置信息和最小跳數(shù)后,，用式（1）可計算出信標(biāo)節(jié)點i與其余信標(biāo)節(jié)點之間的平均跳距：

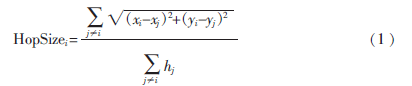
　　其中,，（xi，yi）,，（xj,，yj）分別表示信標(biāo)節(jié)點i、j的坐標(biāo),，hj表示i距j的跳數(shù),。

　　然后，信標(biāo)節(jié)點將平均跳距分組擴(kuò)散至整個網(wǎng)絡(luò)內(nèi),，可通過最小跳數(shù)和式（2）獲取待定位節(jié)點與其他信標(biāo)節(jié)點的間距,。

　　di=HopSizei×hi（2）

　　（3）待定位節(jié)點自身位置的估算

　　已知（xi,，yi）是第i個信標(biāo)節(jié)點的坐標(biāo),，它到待定位節(jié)點M的距離為di，設(shè)（x,，y）是待定位節(jié)點M的坐標(biāo),，則有：

　　將式（3）變換成線性方程組AX=b的形式，其中：

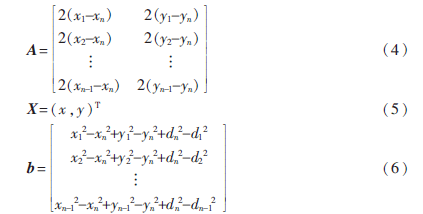
　　最后,，由標(biāo)準(zhǔn)的最小二乘法即可得到節(jié)點M的坐標(biāo)：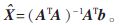

2 改進(jìn)的DV-Hop算法

　　WSN定位問題實質(zhì)上是對非線性方程組進(jìn)行求解,，為NP難解問題。DV-Hop算法在計算待定位節(jié)點和信標(biāo)節(jié)點的間距時,，由于待定位節(jié)點認(rèn)為它到信標(biāo)節(jié)點的平均跳距是相同的,，會造成較大的定位誤差。目前為止,，已有學(xué)者提出用元啟發(fā)式算法對定位后期的位置進(jìn)行優(yōu)化,，如前文提到的BA算法和ASPSO算法。本文采用ASGSO算法對DV-Hop算法求出的待定位節(jié)點位置進(jìn)行優(yōu)化,。

　　2.1 ASGSO算法

　　2.1.1 自適應(yīng)步長調(diào)整策略

　　螢火蟲群優(yōu)化（Glowworm Swarm Optimization,，GSO）算法[10]是一種群智能算法，利用螢火蟲發(fā)光吸引同伴這一現(xiàn)象進(jìn)行模擬,，發(fā)光越強(qiáng)便可吸引越多的同伴,，每個螢火蟲通過移向目標(biāo)區(qū)域內(nèi)最亮螢火蟲尋求最優(yōu)解。

　　原始GSO算法存在易陷入局部最優(yōu)的缺陷,，其計算精度較低,，且最后階段收斂速度較慢,，這些問題與步長密切相關(guān)。尋優(yōu)時螢火蟲的移動步長越大則越容易尋求到全局最優(yōu)解,，但其尋優(yōu)精度隨之降低,，甚至?xí)霈F(xiàn)震蕩；移動步長小會造成尋優(yōu)速度慢,，但尋優(yōu)精度得到提高,。

　　針對此問題提出的ASGSO算法解決了原始GSO算法中存在的問題，有極好的尋優(yōu)能力和尋優(yōu)精度,。引入熒光因子：

　　其中,，Xi為第i只螢火蟲的狀態(tài)，Xext為熒光素濃度最大的螢火蟲的狀態(tài),，dmax為最優(yōu)螢火蟲與剩余螢火蟲的最大距離,。

　　自適應(yīng)步長調(diào)整辦法為：

　　si=smin+（smax-smin）Hi（8）

　　式中，smax和smin為尋優(yōu)步長的最大值和最小值,，Hi為熒光因子,。

　　根據(jù)式（7）、（8）自適應(yīng)變換迭代步長,，當(dāng)螢火蟲個體與目標(biāo)螢火蟲距離較近時,，Hi值減小，則si值相應(yīng)減小,，使用略小的步長si可使螢火蟲接近目標(biāo)個體,，精度得以提高；當(dāng)螢火蟲與目標(biāo)螢火蟲距離較遠(yuǎn)時,，Hi值的增大會造成si值增大,，可使螢火蟲在步長略大時實現(xiàn)快速尋優(yōu)。ASGSO通過靈活調(diào)整搜索步長提升了尋優(yōu)的速度和精度,。

　　2.1.2 算法描述

　　ASGSO算法流程如下：

　　（1）初始化,。n只螢火蟲組成螢火蟲群,，設(shè)定搜索維數(shù)m，感知最大半徑rs及其變化系數(shù),，最大迭代次數(shù)itermax,，熒光素?fù)]發(fā)系數(shù)ρ及其更新率，優(yōu)秀螢火蟲個體數(shù)nt,，原始位置xi（0）,，原始熒光素大小l0和感知范圍r0，原始步長si（0）,，最大步長smax,，最小步長smin,。

　　（2）熒光素更新,。J（xi（t））為迭代位置xi（t）的目標(biāo)函數(shù),。將螢火蟲在t次迭代位置xi（t）相對應(yīng)的J（xi（t））轉(zhuǎn)換成熒光素值li（t）=（1-ρ）li（t-1）+J（xi（t）），螢火蟲選取比自身熒光素高的個體組成鄰域集Ni（t）,，其中,，0<rdi（t）≤rs，rs為螢火蟲的感知半徑,。

　?。?）概率選擇。個體i移至鄰域集個體j的概率pij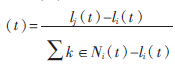,，用輪盤賭選取個體j,。

　　（4）自適應(yīng)步長改變,。利用式（7）計算每個個體的熒光因子,，用式（8）計算出步長值。

　?。?）位置更新,。根據(jù)更新位置。

　?。?）更替決策域,。由rdi（t+1）=min{rs，max{0,，rdi（t）+（ni-|Ni（t）|）}}更新動態(tài)決策域半徑,。

　　（7）迭代結(jié)束,。判斷是否完成所設(shè)定的迭代次數(shù),，如果是則輸出結(jié)果；否則轉(zhuǎn)至步驟（2）,。

　　2.2 基于ASGSO算法的改進(jìn)DV-Hop算法

　　DV-Hop算法進(jìn)行定位時,，由于距離的不確定性導(dǎo)致誤差存在。定位問題的要點是使誤差達(dá)到最小,，即提高定位精度,，因此提出一種基于ASGSO算法的改進(jìn)DV-Hop算法，即ASGSODV-Hop算法,。

　　設(shè)待定位節(jié)點的坐標(biāo)為（x,，y），利用式（2）可得待定位節(jié)點與第i個信標(biāo)節(jié)點的估算間距為di,，信標(biāo)節(jié)點的估計間距與真實間距的偏差為εi,，則式（3）可改為：

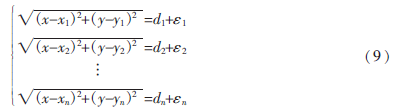
　　通過觀察式（9）可以看出,，當(dāng)（|ε1|+|ε2|+…+|εn|）的值最小時，所求得的未知節(jié)點（x,，y）與真實節(jié)點位置最為接近,。由于信標(biāo)節(jié)點與待定位節(jié)點間的跳數(shù)越多會導(dǎo)致兩者間距的估計偏差越大，故將其跳數(shù)的倒數(shù)當(dāng)作權(quán)重設(shè)置ASGSO算法的適應(yīng)度函數(shù),，如式（10）所示,。完成所設(shè)定的運(yùn)算次數(shù)后即可結(jié)束ASGSO算法，以所尋求的最優(yōu)值當(dāng)作優(yōu)化后的估算值,。

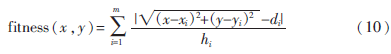
　　其中,，hi為待定位節(jié)點（x，y）與信標(biāo)節(jié)點（xi,，yi）間的跳數(shù),，1/hi為權(quán)重。

3 仿真實驗

　　為評估ASGSODV-Hop算法的性能,，分別對DV-Hop算法改進(jìn)前后進(jìn)行仿真,，分析比對仿真得到的結(jié)果。將若干節(jié)點散播在100 m×100 m正方形感知區(qū)域內(nèi),，信標(biāo)節(jié)點占10%,，待定位節(jié)點占90%。為了降低隨機(jī)性誤差,，在同等參數(shù)條件下進(jìn)行100次仿真,，取其均值作為實驗結(jié)果。

　　本文選取文獻(xiàn)[11]提到的定位誤差作為性能評價指標(biāo),，如式（11）所示：

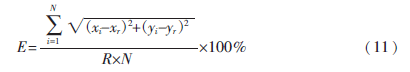
　　其中,，R為通信半徑，（xr,，yr）為待定位節(jié)點的真實坐標(biāo),，（xi，yi）為使用ASGSODV-Hop算法得出的待定位節(jié)點坐標(biāo),，N為待定位節(jié)點的個數(shù),。

　　3.1 算法參數(shù)設(shè)置

　　設(shè)定種群規(guī)模n=50，維數(shù)m=2,，揮發(fā)系數(shù)ρ=0.4，更新率?酌=0.6,，初始熒光素大小l0=5,，感知范圍r0=10，初始步長si（0）=0.03,，變化系數(shù)?茁=0.08,，最大迭代次數(shù)itermax=200,。

　　3.2 算法仿真結(jié)果分析

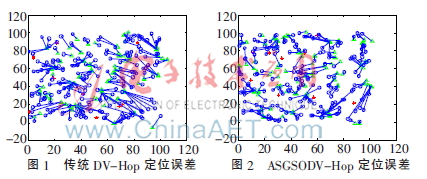
　　將200個節(jié)點隨機(jī)部署在上述網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)中，通信半徑設(shè)置為R=30 m,，圖1和圖2分別為DV-Hop算法和ASGSODV-Hop算法的定位誤差圖,，圖中‘*’表示信標(biāo)節(jié)點，‘o’表示待定位節(jié)點估計位置,，‘▽’表示待定位節(jié)點實際位置,，‘o’和‘▽’之間的連線表示待定位節(jié)點的定位誤差，線段越長,，定位誤差越大,，反之越小。從圖中可看出,，改進(jìn)算法的估計位置和實際位置之間的線段更短,，即它們之間的定位誤差更小。通過DV-Hop算法得出的平均定位誤差為17.48,，定位精度為34.96%,，ASGSODV-Hop算法的平均定位誤差為10.62，定位精度為21.24%,。由此可知ASGSODV-Hop算法的平均定位誤差和定位精度明顯優(yōu)于傳統(tǒng)DV-Hop算法,。

　　在定位技術(shù)中，通信半徑,、節(jié)點數(shù)及網(wǎng)絡(luò)連通度的變化都會影響定位精度,，下面分別討論兩種算法在不同通信半徑、不同信標(biāo)節(jié)點數(shù)以及不同網(wǎng)絡(luò)連通度條件下的定位精度,。

　?。?）不同通信半徑

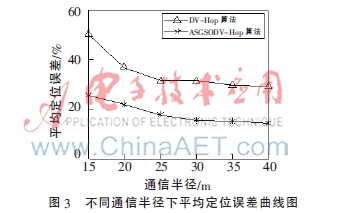
　　圖3表示通信半徑從15 m~40 m時兩種算法的平均定位誤差曲線圖，在區(qū)域內(nèi)隨機(jī)部署200個節(jié)點,，20個信標(biāo)節(jié)點,。從圖中可知，在同樣參數(shù)條件下,，兩種算法的平均定位誤差均隨通信半徑的不斷增加逐漸降低,，并且當(dāng)通信半徑在15 m~30 m范圍內(nèi)時，平均定位誤差下降速率較快,；通信半徑在30 m以后時,，平均定位誤差趨于穩(wěn)定，并且在穩(wěn)定區(qū)域內(nèi),，ASGSODV-Hop算法的平均定位誤差比DV-Hop減小約35.28%,。在整個通信半徑變化區(qū)域內(nèi)，與DV-Hop算法相比較,，ASGSODV-Hop算法的平均定位誤差可降低約43.51%,，使精度明顯提升,。

　　（2）不同節(jié)點數(shù)

　　圖4表示通信半徑為R=30 m,、信標(biāo)節(jié)點數(shù)為20時,，節(jié)點總數(shù)由100變化至400的平均定位誤差曲線。從圖中可看出,，在相同條件下兩種算法的平均定位誤差均隨節(jié)點數(shù)的增大而減小,，并且當(dāng)節(jié)點數(shù)在200~400之間時，待定位節(jié)點誤差趨于穩(wěn)定,。經(jīng)分析可知ASGSODV-Hop算法的平均定位誤差比DV-Hop算法降低了約47.98%,；當(dāng)節(jié)點數(shù)小于200時兩種算法的定位誤差下降幅度較大，此時與傳統(tǒng)DV-Hop算法相比,，ASGSODV-Hop算法的平均定位誤差可下降約52.73%,。

　　（3）不同網(wǎng)絡(luò)連通度

　　由于DV-Hop算法是根據(jù)網(wǎng)絡(luò)連通性來進(jìn)行定位的,，網(wǎng)絡(luò)連通度這個概念一定意義上可反映定位區(qū)域中節(jié)點間的相互位置,、節(jié)點通信半徑以及節(jié)點數(shù)量間的相互關(guān)系。圖5為不同網(wǎng)絡(luò)連通度下兩種算法的平均定位誤差曲線,，從圖中可清晰看出隨著網(wǎng)絡(luò)連通度參數(shù)值的升高定位誤差逐漸減小,，當(dāng)網(wǎng)絡(luò)連通度大于20時，兩種算法的定位誤差值變化都比較平緩,。與傳統(tǒng)DV-Hop算法相比,，ASGSODV-Hop算法的平均定位誤差降低約51.76%。

4 結(jié)論

　　本文在充分研究DV-Hop算法的基礎(chǔ)上,，針對定位精度較低這一缺點,，在無需附加硬件和通信量的條件下采用ASGSO算法對DV-Hop算法的待定位節(jié)點坐標(biāo)進(jìn)行優(yōu)化。通過理論分析和算法仿真實驗證明,，經(jīng)ASGSO算法優(yōu)化后的DV-Hop算法使定位誤差下降約      46.49%,，定位精度得到明顯提高。此外,，ASGSO算法的高效運(yùn)行可有效提高DV-Hop算法在WSN中的適用性,，使其應(yīng)用更為廣泛。

　　參考文獻(xiàn)

　　[1] 鄭軍,，張寶賢.無線傳感器網(wǎng)絡(luò)技術(shù)[M].北京：機(jī)械工業(yè)出版社,，2012.

　　[2] BULUSU N， HEIDEMANN J,， ESTRIN D. GPS-less low cost outdoor localization for very smal devices[J]. IEEE Personal  Communications  Magazine,， 2000，7（5）：28-34.

　　[3] NICULESCU D， NATH B. DV-based positioning in ad hoc networks[J]. Journal of Telecommunication Systems,， 2003，22 （1）：267-280.

　　[4] NICOLESCU D,， NATH B. Ad-Hoc positioxung systems （APS）[C]. Proc.of the 2001 IEEE Global Telecommunications Conference,， San Antonio， USA,， 2001：2926-2931.

　　[5] He Tian,， Huang Chengdu， BRIAN M B,， et al. Range-free localization schemes for large scale sensor networks[C]. In Proceedings of the 9th Annual International Conference on Mobile Computing and Networking,， New York， USA,， ACM Press,， 2003：81-95.

　　[6] 涂巧玲，宋佳,，胡濤.一種加權(quán)的DV-Hop定位改進(jìn)算法[J].通信技術(shù),，2013，46（9）：58-60.

　　[7] 曹欲曉,，張倩,，李艷冰，等.基于蝙蝠算法的DV-Hop定位改進(jìn)[J].計算機(jī)測量與控制,，2015,，23（4）：1273-1275.

　　[8] 李仁和，丁勤,，王洪元,，等.基于自適應(yīng)粒子群算法的改進(jìn)DV-Hop定位算法[J].計算機(jī)與應(yīng)用化學(xué)，2014,，31（10）：1201-1204.

　　[9] 歐陽喆,，周永權(quán).自適應(yīng)步長螢火蟲優(yōu)化算法[J].計算機(jī)應(yīng)用，2011,，31（7）：1804-1807.

　　[10] 呂聰穎.智能優(yōu)化方法的研究及其應(yīng)用[M].北京：中國水利水電出版社,，2014.

　　[11] 張萬里，宋啟祥.遺傳算法的DV-Hop算法改進(jìn)[J].重慶大學(xué)學(xué)報,，2015,，38（3）：159-166.