摘  要： 針對(duì)無芯片RFID多標(biāo)簽難以準(zhǔn)確識(shí)別的問題,，提出一種改進(jìn)型矩陣束算法（Matrix Pencil Method,，MPM）解決其碰撞問題。標(biāo)簽散射場(chǎng)信號(hào)存在早時(shí)和后時(shí)響應(yīng),，散射場(chǎng)信號(hào)極點(diǎn)在早時(shí)響應(yīng)期間處于不穩(wěn)定狀態(tài),，但在后時(shí)響應(yīng)期間趨于穩(wěn)定。算法利用散射場(chǎng)信號(hào)這一特性,，在多標(biāo)簽散射場(chǎng)信號(hào)中應(yīng)用改進(jìn)型矩陣束算法,，根據(jù)后時(shí)響應(yīng)開啟時(shí)間和極點(diǎn)穩(wěn)定程度的不同來區(qū)分各個(gè)標(biāo)簽。實(shí)驗(yàn)中采用多個(gè)方形開槽結(jié)構(gòu)標(biāo)簽來建立模型,。仿真結(jié)果表明,，該算法能夠區(qū)分各個(gè)無芯片RFID標(biāo)簽，基本滿足了對(duì)多標(biāo)簽檢測(cè)準(zhǔn)確性,、穩(wěn)定性等方面的要求,。

　　關(guān)鍵詞： 無芯片RFID；防碰撞,；矩陣束算法（MPM）,；電子標(biāo)簽；散射場(chǎng)

0 引言

　　射頻識(shí)別技術(shù)（RFID）能夠?qū)崿F(xiàn)物與物之間無接觸式信息傳遞,，即閱讀器通過天線與電子標(biāo)簽進(jìn)行數(shù)據(jù)交互,。目前廣泛采用無源有芯或者有源有芯電子標(biāo)簽，但其成本較高,，無芯片RFID標(biāo)簽應(yīng)運(yùn)而生,。因目前RFID防碰撞算法主要針對(duì)有芯片標(biāo)簽[1-3]，均基于閱讀器主動(dòng)控制標(biāo)簽休眠,，而無芯片RFID標(biāo)簽內(nèi)無IC芯片,，只是擁有特定材質(zhì)有限大小的結(jié)構(gòu)，因此大部分RFID防碰撞算法在無芯片RFID的應(yīng)用中失效,。本文利用Carl E. Baum提出的極點(diǎn)展開法（the Singularity Expansion Method,，SEM）[4-5]來研究標(biāo)簽散射場(chǎng)特性[6-8]，進(jìn)一步應(yīng)用改進(jìn)型矩陣束算法解決多個(gè)標(biāo)簽防碰撞問題,，分析算法在無芯片RFID多標(biāo)簽識(shí)別中的有效性,。

1 相關(guān)理論

　　1.1 散射電磁場(chǎng)的SEM建模

　　1971年Carl E. Baum將傳統(tǒng)電路理論中用留數(shù)定理求解瞬態(tài)響應(yīng)的方法推廣到瞬態(tài)電磁場(chǎng)問題處理中，提出了SEM，其理論表明電磁波照射金屬導(dǎo)體時(shí),，瞬態(tài)響應(yīng)后期可以被看成一系列衰減復(fù)指數(shù)和的形式：

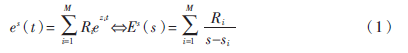
　　其中es（t）為后向散射的時(shí)域信號(hào),，M為極點(diǎn)個(gè)數(shù)，Ri是信號(hào)的留數(shù),，si為信號(hào)的復(fù)極點(diǎn),，一般取si=?琢i+jwi（?琢i取負(fù)數(shù)，稱為阻尼因子或衰減因子,；wi取正數(shù),，為自然諧振角頻率）。由于散射信號(hào)是實(shí)數(shù),，所以極點(diǎn)總是以共軛對(duì)的形式存在,。

　　同樣，多標(biāo)簽散射場(chǎng)也具有相同特性,，若查詢信號(hào)頻帶覆蓋了多個(gè)標(biāo)簽的自然諧振頻率,，由標(biāo)簽感應(yīng)產(chǎn)生的后向散射回波信號(hào)電場(chǎng)es時(shí)域表示為：

　　式（2）和（3）中，r和t分別表示檢測(cè)回波信號(hào)的位置和時(shí)間,，M為所查詢標(biāo)簽個(gè)數(shù),，em（Em）為第m個(gè)標(biāo)簽的早時(shí)響應(yīng)，U（t）為單位階躍函數(shù),，tm和Nm分別為第m個(gè)標(biāo)簽的后時(shí)響應(yīng)開啟時(shí)間和極點(diǎn)共軛對(duì)數(shù)目,，第m個(gè)標(biāo)簽的第n個(gè)復(fù)極點(diǎn)和留數(shù)分別為sm，n和Rm,，n,。

　　在復(fù)頻域中，信號(hào)的特征通過極點(diǎn)和留數(shù)來表征,，而極點(diǎn)和留數(shù)的大小只與金屬導(dǎo)體的形狀有關(guān),，與激勵(lì)源無關(guān)。所以標(biāo)簽結(jié)構(gòu)與極點(diǎn)呈現(xiàn)出一一對(duì)應(yīng)關(guān)系,，標(biāo)簽的檢測(cè)與識(shí)別的關(guān)鍵技術(shù)之一是從es（t）中提取信號(hào)的極點(diǎn),。

　　1.2 改進(jìn)矩陣束算法（MPM）

　　目前，極點(diǎn)提取算法有多種,，比如Prony方法,、矩陣束算法[9-12]、短時(shí)矩陣束算法[13]等,。實(shí)際情況中,，Prony算法抗噪性能差，矩陣束算法采用內(nèi)積形式研究極點(diǎn)提取問題,，使抗噪能力有所提高,。

　　在多標(biāo)簽防碰撞算法中,，對(duì)傳統(tǒng)矩陣束算法進(jìn)行以下改進(jìn)：如圖1所示，在散射場(chǎng)時(shí)域信號(hào)es（r,，t）中加一寬度為Tw的虛擬窗口，窗口每次滑動(dòng)?駐t,，同時(shí)應(yīng)用一次矩陣束算法（MPM）計(jì)算極點(diǎn)和留數(shù),，直到窗口內(nèi)無數(shù)據(jù)。由于早時(shí)響應(yīng)的存在,，早時(shí)期間極點(diǎn)處于不穩(wěn)定狀態(tài),，而后時(shí)響應(yīng)期間極點(diǎn)會(huì)保持穩(wěn)定，根據(jù)穩(wěn)定的極點(diǎn)識(shí)別出標(biāo)簽,。

2 多標(biāo)簽防碰撞設(shè)計(jì)及仿真結(jié)果

　　2.1防碰撞標(biāo)簽結(jié)構(gòu)的建立

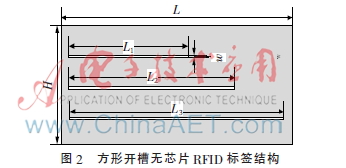
　　為了研究無芯片RFID多標(biāo)簽防碰撞相關(guān)問題,，利用方形開槽結(jié)構(gòu)標(biāo)簽建立仿真模型，如圖2所示（尺寸單位：mm）,。槽的長度決定諧振頻率和衰減因子,，標(biāo)簽1尺寸：L=45，H=10,，L1=27,，L2=30，L3=33,，w=0.2,；標(biāo)簽2尺寸：L=30，H=10,，L1=18,，L2=20，L3=24,，w=0.2,。

　　實(shí)驗(yàn)采用電磁仿真軟件FEKO 5.5分別對(duì)標(biāo)簽1標(biāo)簽2進(jìn)行仿真，得到其在50 MHz~10 GHz頻域散射場(chǎng)信號(hào)數(shù)據(jù),，采樣數(shù)據(jù)點(diǎn)數(shù)均為1 024,。如圖3所示，標(biāo)簽1散射場(chǎng)極點(diǎn)分布大約在5.2 GHz,、5.9 GHz,、6.9 GHz，標(biāo)簽2散射場(chǎng)極點(diǎn)分布大約在3.95 GHz,、4.2 GHz,、4.7 GHz。最后將標(biāo)簽1和標(biāo)簽2同時(shí)進(jìn)行仿真,，并設(shè)置兩標(biāo)簽間隔距離為2 m,。

　　2.2 無芯片RFID標(biāo)簽防碰撞的實(shí)現(xiàn)

　　2.2.1 改進(jìn)型矩陣束算法參數(shù)選擇

　　利用改進(jìn)型矩陣束算法提取散射場(chǎng)信號(hào)極點(diǎn)時(shí)，需要選擇合適的窗口寬度Tw和每次滑動(dòng)的寬度t。窗口寬度Tw的選擇可以根據(jù)采樣點(diǎn)數(shù)N和時(shí)間總長T來決定,，即Tw=T/N,，此處Tw取0.04 ns較合適。經(jīng)過多次實(shí)驗(yàn),，一般t≤Tw時(shí),，極點(diǎn)提取的效果比較理想，此處t取0.01 ns,。窗口寬度Tw和滑動(dòng)寬度t的選取直接影響到極點(diǎn)提取的精度,，也將會(huì)影響多標(biāo)簽識(shí)別的準(zhǔn)確性。

　　2.2.2 無芯片RFID多標(biāo)簽的識(shí)別

　　標(biāo)簽結(jié)構(gòu)如圖2所示的標(biāo)簽1和標(biāo)簽2的混合散射場(chǎng)時(shí)域信號(hào)如圖4所示,，應(yīng)用改進(jìn)型矩陣束算法提取其極點(diǎn),，獲得極點(diǎn)的虛部與時(shí)間的關(guān)系（即諧振頻率與時(shí)間的關(guān)系），如圖5所示,。

　　從圖5中可以看出,，早時(shí)響應(yīng)期間（t<Ton1和7 ns<t<Ton2）散射場(chǎng)信號(hào)極點(diǎn)不穩(wěn)定，后時(shí)響應(yīng)期間極點(diǎn)趨于穩(wěn)定,，同時(shí)從諧振頻率與時(shí)間關(guān)系圖中可以獲知：標(biāo)簽1的諧振頻率為5.2 GHz,、5.9 GHz、6.9 GHz（圖中Ton1<t<6 ns期間）,；標(biāo)簽2的諧振頻率為3.95 GHz,、4.2 GHz、4.7 GHz （圖中t>Ton2期間）,。由此可知,，根據(jù)標(biāo)簽后時(shí)響應(yīng)開啟時(shí)間Ton的不同，標(biāo)簽可以被準(zhǔn)確區(qū)分,，解決了后時(shí)響應(yīng)開啟時(shí)間不同的多標(biāo)簽防碰撞問題,。

3 結(jié)束語

　　本文將矩陣束算法進(jìn)行改進(jìn)并應(yīng)用于無芯片RFID多標(biāo)簽防碰撞的研究中，在研究防碰撞的同時(shí)找出了標(biāo)簽的后時(shí)響應(yīng)開啟時(shí)間,，根據(jù)各個(gè)標(biāo)簽散射場(chǎng)后時(shí)響應(yīng)開啟時(shí)間的不同,，從標(biāo)簽散射場(chǎng)的諧振頻率和時(shí)間關(guān)系中，準(zhǔn)確地識(shí)別各個(gè)標(biāo)簽,。此種方法對(duì)無芯片標(biāo)簽的識(shí)別以及多標(biāo)簽防碰撞有一定參考價(jià)值,。但是此種方法有一定局限性，即針對(duì)各個(gè)標(biāo)簽距離閱讀器距離幾乎相等（后向散射開啟時(shí)間近似相同）時(shí),，標(biāo)簽將無法被準(zhǔn)確識(shí)別,。

參考文獻(xiàn)

　　[1] HWANG T W， LEE B G,， KIM Y S,， et al. Improved anti-collision scheme for high speed identification in RFID system[C]. Proceeding of the First International Conference on Innovative Computing,， Information and Control， 2006：449-452.

　　[2] 單承贛,，余春梅,，王聰聰.改進(jìn)的二進(jìn)制查詢樹的RFID標(biāo)簽防碰撞算法[J].合肥工業(yè)大學(xué)學(xué)報(bào)（自然科學(xué)版），2008,，31（11）：1081-1084.

　　[3] 李瑞林,，劉嵩巖，茍鵬飛,，等.RFID標(biāo)簽防碰撞研究[J].微機(jī)處理，2008,，29（5）：100-103.

　　[4] BAUM C E. On the singularity expansion method for the solution of electromagnetic interaction problems[J]. Interaction Note 1971,，88（12）：1-111.

　　[5] BAUM C E， ROTHWELL E J,， CHEN K M,， et al. The singularity expansion method and its application to target identification[J]. Proceedings of the IEEE， 1991,，79（10）：1481-1492.

　　[6] REZAIESARLAK R,， MANTEGHI M. Mathematical representation of scattered fields from chipless RFID tags[M]. Rerlin： Springer International Publishing， 2015.

　　[7] LI Q,， ILAVARASAN P,， ROSS J E， et al. Radar target identification using a combined early-time/late-time e-pulse technique[J]. IEEE Antennas and Propagation,，1998,， 46（9）： 1272-1278.

　　[8] CHAUVEAU J， BEAUCOUDREY N D,， SAILLARD J. Characterization of radar targets in resonance domain with a reduced number of natural poles[C]. Radar Conference,， 2005 European. IEEE Conference Publications，2005：69-72.

　　[9] WANG S,， GUAN X,， WANG D， et al. Application of Matrix Pencil Method for estimating natural resonances of Scatters[J]. Electronics Letters,， 2007,， 43（1）：3-5.

　　[10] SARKAR T K， PARK S,， KOH J W,， et al. Application of the Matrix Pencil Method for estimating the SEM（Singularity Expansion Method） poles of source-free transient response from multiple look directions[J]. Antennas and Propagation， IEEE Transactions on,， 2000,，48（4）：612-618.

　　[11] 徐利,，鄒傳云，陳民,，等.基于矩陣束算法的極點(diǎn)提取分析[J].通信技術(shù),，2012，45（6）：58-60.

　　[12] SARKAR T K,， PEREIRA O. Using the Matrix Pencil Method to estimate the parameters of a sum of complex exponentials[J]. IEEE Antennas and Propagation Magazine,，1995，37（1）：48-55.

　　[13] REZAIESARLAK R,， MANTEGHI M. Short-time Matrix Pencil Method for chipless RFID detection applications[J]. Antennas and Propagation,， IEEE Translations on， 2013,，5（61）：2801-2806.