李濤
(四川大學 計算機學院，四川 成都 610065)
摘要：傳統(tǒng)Retinex算法中,，從圖像中完全去除亮度分量而使用反射分量來增強效果,。通常圖像光照變化并非平緩，使得結果圖像視覺效果缺乏協(xié)調,。對此提出一種改進的Retinex算法,，通過再處理亮度分量，得到平緩的亮度圖像并補償到反射分量從而改善增強效果,，使用均值模版代替高斯模版以減少計算的時間,，同時利用拉普拉斯算子加入圖像邊緣細節(jié)特征。實驗通過處理低對比度,、低亮度的X光射線將改進的Retinex方法與其他各種增強算法進行對比。對實驗結果的定性和定量分析表明了該改進算法的有效性,。
關鍵詞：多尺度Retinex,；均值模版；平滑光照,；拉普拉斯算子
0引言
圖像增強是圖像分析,、圖像分割等其他圖像處理的預處理，其目標是滿足人眼的需要有選擇性地強調或者抑制圖像中的某些信息［1］,。目前,，有許多的增強方法經常出現在各個應用中,，例如伽馬校正、直方圖均衡化和小波變換等［2］,，對圖像增強的發(fā)展起到了一定的引導作用,，但各自表現出明顯的不足。1977年,，LAND E H根據人類視覺中對光照和色彩感知提出了Retinex模型［3］,。Retinex理論就是去除圖像中亮度信息而保留反射信息來恢復物體的原始信息，從而達到增強效果,。然而,，當圖像中光照分布不均勻或者光照不是平緩變化時，僅僅通過濾波器得到的反射分量不能完全滿足要求,。
針對Retinex算法存在的一些不足,，通過對亮度分量進行濾波處理以補償增強后的圖像；算法過程中存在大量的卷積操作,，大大降低了算法運算效率,，根據大尺度高斯模版的均值特性，使用均值模版代替高斯模版對圖像進行濾波操作,；最后通過拉普拉斯算子增加圖像的細節(jié)信息,。
1Retine增強算法理論
根據Retinex理論將圖像視為物體亮度分量L(x,y)和反射分量R(x,y)，則真實圖像函數I(x,y)表達式為：
I(x,y)=R(x,y)*L(x,y)(1)
LAND E H在此基礎上擴展提出中心/環(huán)繞Retinex算法［4］（即局部Retinex）,，JOBSON D J［5］等人在中心/環(huán)繞Retinex的基礎上,，提出了單尺度的Retinex算法，該算法的數學公式為：
R(x,y)=logI(x,y)－log［I(x,y)*F(x,y)］(2)
其中,，R(x,y)表示輸出的圖像,；*為卷積運算；F(x,y)表示中心/環(huán)繞函數,，一般采用高斯函數,，可以達到很好的增強效果。環(huán)繞函數F(x,y)表達式為：
其中,，標準差σ即為尺度參數,。當σ取值較小時，能夠很好地實現動態(tài)范圍壓縮,，圖像局部信息較為突出,，偏暗區(qū)域的邊緣細節(jié)能夠得到較好的增強，但是會出現顏色失真現象,；當σ取值較大時,，圖像整體和顏色保真效果較好，圖1肋骨圖像高斯模版和均值模版濾波比較圖但是動態(tài)壓縮能力與細節(jié)增強效果較差。K是歸一化因子,，使得：
F(x,y)dxdy=1(4)
由式（4）可以看出,，單尺度Retinex算法的增強效果主要依賴于高斯函數標準差σ的選取，單一的σ取值難以同時實現動態(tài)范圍壓縮,、局部信息突出和較好的顏色保真效果,。在此基礎上JOBSON D J進一步提出了多尺度Retinex算法。
多尺度Retinex算法就是通過不同尺度的環(huán)繞函數對圖像進行處理,，可以看作多個不同尺度的單尺度Retinex線性加權求和,，其表達式為：
其中，k表示環(huán)繞函數的個數,，Wi表示不同尺度環(huán)繞函數的加權系數,。在實際環(huán)境中，環(huán)繞函數的標準差一般選取大中小3個尺度,，而權值Wi可以根據實際需求側重點的不同而選取,，在通常情況下，每個權值都選擇相同的1/3比較合適,。多尺度Retinex算法一定程度上兼顧了圖像的整體效果和局部突出,，又保證了動態(tài)范圍壓縮和色彩的一致性。
2多尺度Retinex算法的改進
2.1利用均值模版代替高斯模版
由式(5)可以看出,，多尺度Retinex算法需要計算每個尺度的高斯模版與原始圖像的卷積,，而對于尺度較大的模版做卷積運算的計算量非常大，這大大地影響了算法的效率,。
當高斯模版的尺度選取較大時,，其高斯模版加權矩陣中的權值非常小，并且數值大小均很接近［6］,。對于尺度大小為129×129的高斯模版,，其權值的變化范圍為0.561 4×10－4~0.621 9×10－4，從數值上可以看出,，權值最大值與最小值之間的差異僅為0.605×10－5,，因此如果將高斯模版中這些變化差異不大的權值使用固定值代替，會使得卷積運算變得簡化,。高斯模版中權值相加的和近似為1,，采用均值模版的思想，將權重平均分配到每一個數值上［7］,。針對上面的129×129模版,，計算1/1292，得到的結果近似為0.600 9×10－4,，選用這個數值代替高斯模版中的數值，將高斯模版權值轉換為固定值進行計算。
選擇低亮度,、低對比度的肋骨圖像分別使用高斯模版和均值模版進行處理,。肋骨圖像的大小為100 4×100 4。如圖1所示,，當模版選用129×129時,，從主觀上看兩種濾波后的效果幾乎沒有差異，而當模版選用33×33時,，兩種濾波效果差異也并不大,，因此可以采用均值模版代替大尺度的高斯模版。
2.2保留部分亮度分量補償目標圖像
在引言中提到過,，傳統(tǒng)的Retinex算法將過濾得到的亮度分量從原始圖像中完全移除,。由式(1)的等價公式得到：
R(x,y)=logL(x,y)R(x,y)L(x,y)R(x,y)≈logR(x,y)R(x,y)(6)
式（6）中，（x,y）為環(huán)繞加權平均值,，即Retinex實際是當前點亮度與四周環(huán)繞加權平均亮度的比值,，符合人眼視覺感知的神經生理學機制［8］。若當前點亮度與四周環(huán)繞光照強度基本相同,，或光照變換緩慢,，即公式約等號成立。然而更多情況下圖像并不滿足約等號成立的條件,，對于光照變換不平緩的區(qū)域不能完全消除光照的影響［9］,。
低頻部分L(x,y)代表著灰度級變化緩慢的區(qū)域，因此,，可以過濾由原始圖像得到的亮度分量［10］,保留原始圖像中部分的亮度信息,。在Retinex算法中，亮度圖像由低通濾波得到,，其公式為：
L(x,y)=I(x,y)*F1(x,y)(7)
F1(x,y)為第一次過濾的環(huán)繞函數,，L(x,y)就是原始圖像中的亮度信息。由于亮度不均勻,，因此L(x,y)中灰度變化仍然是動態(tài)的,，而這些灰度動態(tài)變化的區(qū)域正好就是原始圖像中亮度不均勻的區(qū)域。于是再次過濾L(x,y),，其公式為：
L1(x,y)=L(x,y)*F2(x,y)(8)
F2(x,y)為二次過濾的環(huán)繞函數,。對于F1(x,y)和F2(x,y)的濾波模版，本文選用上一節(jié)介紹的均值模版,?？梢酝ㄟ^調整模版大小，消除L(x,y)中高頻的部分,，從而得到相對均衡的亮度L1(x,y),，對圖像亮度補償達到良好的視覺效果,。
圖2(a)是lena圖像過濾得到的亮度部分，可以看出來它是不均勻的,，而圖2(b)經過兩次過濾后得到的L1(x,y),，很明顯相對于圖2(a)在亮度更加平緩。這表明通過二次過濾能夠修正亮度不均勻區(qū)域,，進而得到相對均衡的亮度,。
2.3圖像邊緣細節(jié)增強
為每一個像素進行同比增強,，則增強后的圖像的邊界和輪廓會比較模糊,，因為這種增強方式減小了相鄰像素點之間的灰度差異。而人類視覺系統(tǒng)有增強邊緣對比度的機制［11］,，當人眼觀察圖像中兩塊亮度不同的區(qū)域時,，若邊緣處對比度增高，會產生強烈的對比和反差,，使得圖像輪廓更加清晰,。拉普拉斯算子可以保留像素之間的灰度差異，增強灰度突變處的對比度,，在保留圖像背景的前提下突顯圖像的邊緣細節(jié)信息,。為了更適合于數字圖像處理，使用離散的拉普拉斯算子的模版形式,。圖3所示為兩種常見的拉普拉斯模版,。圖像的邊緣就是那些灰度發(fā)生跳變的區(qū)域，所以拉普拉斯模版有利于突出這些邊緣細節(jié)信息,。
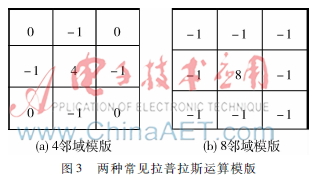
實驗中筆者采用4鄰域拉普拉斯運算模版,。將拉普拉斯模版與原始圖像做卷積運算，再用原圖像減去卷積結果得到圖像邊緣影像,，其公式如下：
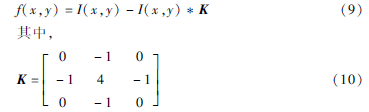
3改進的MSR算法描述與實驗
3.1改進的MSR算法描述
根據Retinex理論［12］,，通過分析與改進，本文的算法可以大致分為以下步驟：
?。?)根據圖像選取適當的均值模版進行濾波處理,，分別得到亮度分量L(x,y)、反射分量R(x,y),。
?。?)對L(x,y)再次進行過濾操作，得到均衡的亮度L1(x,y),，補償R(x,y)得到增強圖像R1(x,y),。
（3)通過式(9)用拉普拉斯模版對原始圖像進行處理,，得到圖像邊緣細節(jié)信息,。
?。?)將增強后的圖像與邊緣圖像疊加，并拉伸修正到顯示器正常顯示范圍,，得到最終的增強圖像,。
3.2實驗結果及分析
實驗對X射線脊柱和頸椎圖像［13］進行增強處理,，圖像大小為1 004×1 004,，分別采用伽馬校正、MSR算法以及本文改進的算法進行處理比較,。
圖4為不同算法的增強效果對比,。從圖4可以看出，不同的增強方法都使得圖像視覺效果得到改善［14］,。伽馬校正［15］一定程度上增強了圖像的對比度和亮度,，但增強的圖像整體較暗且模糊，視覺效果依然很差,；MSR增強算法提高了圖像的亮度,、對比度，但圖像的邊緣信息較差,，同時層次感有所降低,；本文的算法有效地解決了MSR算法的缺點，保留了圖像的邊緣信息,，能夠清晰顯示出骨骼的輪廓,。
圖4從主觀的角度對比分析了幾種增強算法的優(yōu)劣，下面通過計算圖像的信息熵［16］,，定性地分析比較處理后的效果,，如表1、表2所示,。
從表1中可以看出,，MSR算法和本文算法處理后圖像信息熵得到了提高，而本文算法提高得更多,。本文采用均值模版代替高斯模版,，減少了MSR算法中大量的卷積運算，從表2看出在運算時間上有一定程度的提升,，且圖像越大,，提升越明顯。雖然文章加入拉普拉斯算子增加圖像邊緣信息消耗了一定的時間,，但從信息熵和運行時間來看,，本文算法對MSR算法的改進都有著明顯的效果。
4結論
通過多尺度Retinex算法的分析以及實現,，發(fā)現MSR算法存在著灰度級不均勻,，細節(jié)特征模糊等不足,，于是通過平緩亮度圖像補償反射分量，再運用拉普拉斯算子增加圖像邊緣對增強效果進行改善,。實驗結果較好地說明了改進的算法能夠對亮度較差且光照不均勻,、對比度不高的圖像進行有效的增強，增強后的圖像亮度和對比度明顯提高,，圖像細節(jié)信息得到提升,，圖像邊緣更加清晰，更加符合人眼視覺效果,。
參考文獻
?。?］ 陳炳權，劉宏立,，孟凡斌.數字圖像處理技術的現狀及發(fā)展方向［J］.吉首大學學報(自然科學版),，2009,30(1):6370.
［2］ 趙曉霞,，王汝琳.改進的多尺度Retinex算法及其應用［J］.計算機工程,，2011,37(6):209211.
［3］ LAND E H.The Retinex theory of color vision［J］.Scientific American,1977,237(6):108128.
?。?］ LAND E H.An alternative technique for the computation of the designator in the Retinex theory of color vision［J］.Proceedings of the National Acaclemy of Sciences,1986,83(10):30783080.
?。?］ JOBSON D J,RAGMAN Z,WOODELL G A. Properties and performance of a center/surround Retinex［J］.IEEE Transactions on Image Processing,1997,6(3):451462.
［6］ 王科俊,，熊新炎,，任楨,等.基于窗口無關均值濾波的MSR圖像增強［J］.哈爾濱工業(yè)大學學報，2010,42(9):14671471.
?。?］ 陳琛,，張建州.改進的多尺度Retinex醫(yī)學X射線圖像增強算法［J］.計算機工程與應用，2015,51(9):191-195.
?。?］ 曾強,，何士剛.視網膜中的自主感光神經節(jié)細胞［J］.生物物理學報，2011(5)：387394.
?。?］ 唐亮,，謝維信，黃建軍,等.城市航空影像中基于模糊Retinex的陰影消除［J］.電子學報,2005,33(3):500503.
?。?0］ Wang Wen, Li Bo, Zhang Jin, et al. A fast multiscale Retinex algorithm for color image enhancement［C］. Proceedings of the 2008 International Conference on Wavelet Analysis and Pattern Recognition, Hong Kong: IEEE,2008:3031.
?。?1］ RAHMAN Z U, JOBSON D J, WOODELL G A. Investigating the relationship between image enhancement and image compression in the context of the multiscale retinex［J］. Journal of Visual Communication & Image Representation,2011,22(3):237250.
［12］ 王彥臣,，李樹杰,，黃廉卿.基于多尺度Retinex的數字圖像X光圖像增強方法研究［J］.光學精密工程,2006,14(1):7076.
［13］MOREL J M, PETRO A B, SBERT C. A PDE formalization of retinex theory［J］. IEEE Transctions on Image Processing,2010,19(11):28252836.
?。?4］ 李錦,，王俊平,，萬國挺,等.一種結合直方圖均衡化和MSRCR的圖像增強新算法［J］.西安電子科技大學學報(自然科學版)，2014,41(3):103109.
?。?5］ 彭國福,，林正浩.圖像處理中Gamma校正的研究和實現［J］.電子工程師，2006,32(2)：3032.
?。?6］ 吳成茂.一種新信息熵定義及其在圖像分割中的應用［J］.西安郵電學院學報,，2009,14(1):7279.