孔祥昆,，于萬波

　　（大連大學(xué) 信息學(xué)院,，遼寧 大連 116622）

       摘要：利用線性函數(shù)迭代系統(tǒng)進(jìn)行迭代可以繪制出樹與山等自然景物,，而非線性系統(tǒng)在這方面的研究結(jié)果相對較少。本文利用輔助函數(shù)與一個(gè)隨機(jī)生成的多項(xiàng)式函數(shù)構(gòu)成動(dòng)力系統(tǒng),，其中輔助函數(shù)具備類似正弦函數(shù)的性質(zhì),，而多項(xiàng)式函數(shù)只含有二次項(xiàng)或者一次項(xiàng)，通過繪制分形圖等方法對系統(tǒng)的混沌特性進(jìn)行分析,，結(jié)果表明,，一組三維正弦函數(shù)與兩個(gè)三維多項(xiàng)式函數(shù)構(gòu)造的動(dòng)力系統(tǒng)是混沌的概率很高，通過迭代可以得到眾多的具有觀賞和實(shí)用價(jià)值的三維吸引子,。除了可以輔助繪制吸引子圖形外,，這種構(gòu)造混沌的方法也是混沌理論研究的一個(gè)實(shí)例。

　　關(guān)鍵詞：混沌,；吸引子,；曲面；迭代

　　0引言

　　近年來,，研究人員對函數(shù)迭代系統(tǒng)（Iterated Function System）進(jìn)行了深入的研究［1］,，取得了許多研究成果。例如，研究人員使用線性迭代系統(tǒng)繪制出樹,、山等自然景物，從而誕生了分形幾何這一新的學(xué)科分支,；在非線性函數(shù)迭代的研究方面得到了著名的Julia集合與Mandelbrot集合等研究成果［2］,。此外還有M.F.Barnsley研究得出的拼貼定理［3］。在其他各個(gè)學(xué)科領(lǐng)域中,，都有關(guān)于迭代系統(tǒng)的經(jīng)典實(shí)例,，例如，由簡單多項(xiàng)式函數(shù)構(gòu)成的描述大氣運(yùn)動(dòng)的Lorenz系統(tǒng)［4］,，這一系統(tǒng)促使研究人員開始對混沌進(jìn)行深入研究,；化學(xué)反應(yīng)中也有著許多混沌系統(tǒng)，如Brussels振子［5］,；一些人工神經(jīng)網(wǎng)絡(luò)中的系統(tǒng)等也可以出現(xiàn)混沌［6］,。對于什么樣的函數(shù)構(gòu)成動(dòng)力系統(tǒng)才可以出現(xiàn)混沌，文獻(xiàn)［7］選擇插值擬合曲面進(jìn)行研究,。文獻(xiàn)［7］研究發(fā)現(xiàn),，如果式（1）

　　中的曲面f(x,y)是雙二次有理貝塞爾（曲面）函數(shù)，而另外一個(gè)曲面g(x,y)是隨機(jī)生成的多項(xiàng)式曲面,，則式 (1)所示的動(dòng)力系統(tǒng)出現(xiàn)混沌的概率可以大于十分之一,。在此基礎(chǔ)上，文獻(xiàn)［89］研究了三角函數(shù)曲面與隨機(jī)多項(xiàng)式曲面構(gòu)成動(dòng)力系統(tǒng)的混沌特性,，發(fā)現(xiàn)在一定的參數(shù)區(qū)間內(nèi),，出現(xiàn)混沌的概率可以超過90%，所以三角函數(shù)是一種（目前來看）最好的輔助函數(shù),。文獻(xiàn)［9］使用三維輔助函數(shù),，例如三維三角函數(shù)、小波函數(shù),、Logistic函數(shù)等與兩個(gè)三維隨機(jī)多項(xiàng)式函數(shù)構(gòu)成動(dòng)力系統(tǒng),，研究發(fā)現(xiàn)其是否出現(xiàn)混沌與三維函數(shù)的截面形狀有直接關(guān)系。

　　本文在以上研究基礎(chǔ)上,，進(jìn)一步研究了什么樣的曲面構(gòu)成的動(dòng)力系統(tǒng)是混沌的,，以及如何使用迭代函數(shù)系統(tǒng)生成更多的圖形圖案，以用于工業(yè)設(shè)計(jì),、動(dòng)漫設(shè)計(jì)等領(lǐng)域,。

1二維正弦函數(shù)與隨機(jī)多項(xiàng)式函數(shù)構(gòu)成動(dòng)力系統(tǒng)

　　作為輔助函數(shù)，正弦函數(shù)具有很好的特性,，振蕩并占有一定的空間,，與另外一個(gè)二次隨機(jī)多項(xiàng)式構(gòu)成動(dòng)力系統(tǒng)，如式（2）所示。使用該動(dòng)力系統(tǒng)進(jìn)行迭代,，能夠構(gòu)造出大量的混沌系統(tǒng)［8］,。

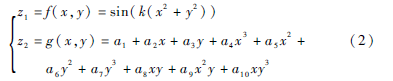
　　本文進(jìn)一步研究發(fā)現(xiàn)，正弦函數(shù)與其他形式的隨機(jī)多項(xiàng)式構(gòu)成動(dòng)力系統(tǒng)也可以很容易出現(xiàn)混沌,，并且能夠產(chǎn)生大量獨(dú)特的吸引子圖形,。

　　1.1二維正弦函數(shù)與沒有xy項(xiàng)的隨機(jī)二次函數(shù)構(gòu)成動(dòng)力系統(tǒng)

　　式（2）中系數(shù)是隨機(jī)生成的，其中某個(gè)系數(shù)為0的可能性比較小,。如果令某些系數(shù)為0,，則：

　　令式（3）中的k=3.141 59，隨機(jī)生成g(x,y)表達(dá)式的系數(shù),，其為-1~1之間的數(shù),。為了確保迭代能夠正常進(jìn)行，將多項(xiàng)式g(x,y)函數(shù)值調(diào)整到-1~1之間,。調(diào)整方法是：首先計(jì)算多項(xiàng)式函數(shù)在［0, 1］× ［0, 1］區(qū)域上的最大值g(x,y)max和最小值g(x,y)min,，然后使用式（4）進(jìn)行調(diào)整：

　　調(diào)整之后的函數(shù)經(jīng)過仿真模擬繪制出吸引子圖形，如圖1所示,。

　　得到4個(gè)吸引子的系數(shù)a0,，a1，a2,，a3,，a4分別為:

　　(a)0.401 3，0.965 4,，0.613 3,，0.407 1，-0.030 1;

　　(b)0.831 9,，0.204 0,，-0.492 9，0.746 9,，0.026 8;

　　(c)0.656 1,，0.835 1，-0.773 8,，0.624 3,，0.816 5;

　　(d)-0.086 1，0.576 3,，-0.437 9,，-0.550 4，0.817 7,。

　　當(dāng)式（3）中g(shù)(x,y)的常數(shù)項(xiàng)與一次項(xiàng)系數(shù)都為0時(shí),，如式（5）所示,，這種情形下，也易于出現(xiàn)混沌,，但是因?yàn)閰?shù)少,，所以吸引子樣式減少，很容易得到一些中間過渡的吸引子圖形,，如圖2所示,，其中f(x,y)的參數(shù)k=3.141 59。

　　系數(shù)分別為:(a)0.756 6,，0.283 3;(b)0.369 3，0.957 0;(c)-0.812 1,，0.300 1;(d)-0.990 6,，0.206 2。

　　實(shí)驗(yàn)結(jié)果發(fā)現(xiàn),，當(dāng)g(x,y)沒有平方項(xiàng)或有xy項(xiàng)時(shí),，如式（6）與式（7），不易出現(xiàn)混沌,。

　　當(dāng)g(x,y)有常數(shù)項(xiàng),、一次項(xiàng)、平方項(xiàng),，也有立方項(xiàng)時(shí),，如式（8）所示，可以繪制出眾多吸引子,，如圖3所示,。

　　f(x,y)=sin(k(x2+y2))

　　g(x,y)=a0+a1x+a2y+a3x2+a4y2+a5x3+a6y3 （8）

　　得到的吸引子系數(shù)分別為：

　　(a)-0.120 2，0.866 8,，0.366 7,，0.678 5，0.257 6,，-0.574 9,，-0.732 5；

　　(b)-0.535 3,，0.609 7,，0.816 8，-0.521 4,，-0.900 5,，-0.536 2，-0.843 2,；

　　(c)-0.248 2,，-0.980 2,，-0.160 3，0.587 7,，0.839 9,，0.507 3，0.689 4,；

　　(d)0.867 7,，-0.725 6，0.043 2,，0.790 4,。

　　由圖3可知，當(dāng)式（8）中g(shù)(x,y)=a0+a1x+a2y+a3x3時(shí),，出現(xiàn)混沌吸引子的概率小一些（大約在0.5）,，不過會(huì)出現(xiàn)一些面積比較大的混沌，如圖2（d）所示,。

　　為了提升出現(xiàn)混沌吸引子的概率,，把式（8）中的f(x,y)調(diào)整為f(x,y)=sin(k1 x2 + k2 y2)，就會(huì)很容易出現(xiàn)混沌,，如圖4所示,。　

　　此時(shí),，吸引子系數(shù)分別為：

　　(a)0.539 8,，-0.249 9，0.646 8,，-0.906 7,，0.195 8，0.898 3,，-0.422 4,，k1=3.141 59,k2=3.8;

　　(b)0.332 2，-0.738 1,，-0.809 2,，-0.970 3，-0.423 6,，0.633 5,，0.971 0，k1=3.141 59,k2=2.8,。

　　1.2二維正弦函數(shù)與隨機(jī)多項(xiàng)式函數(shù)迭代出現(xiàn)混沌的條件分析

　　周期點(diǎn)在混沌研究中有著重要的作用,。如果一個(gè)系統(tǒng)沒有不動(dòng)點(diǎn)（一周期點(diǎn)）和二周期點(diǎn)，那它就不是LiYorke混沌的,，也不是Devaney混沌的,。另外文獻(xiàn)［8］分析了二維Devaney混沌產(chǎn)生的必要條件與周期點(diǎn)處的導(dǎo)數(shù)的乘積的絕對值之間的關(guān)系,。

　　由文獻(xiàn)［8］結(jié)論1和結(jié)論2可知，在構(gòu)造混沌曲面迭代時(shí),，周期點(diǎn)處不能太平坦,。這里所說的混沌需要滿足Devaney混沌定義中的遍歷性，即對定義域內(nèi)任何兩個(gè)開集U,V∈χ,存在自然數(shù)k,。

　　結(jié)論1動(dòng)力系統(tǒng)如式（1）所示,，如果二元函數(shù)f(x,y)與g(x,y)定義域?yàn)椋?,1］×［0,1］，值域是［0,1］,，在定義域內(nèi)存在關(guān)于x,y的偏導(dǎo)數(shù),。如果f(x,y)與g(x,y)構(gòu)成的動(dòng)力系統(tǒng)是混沌的，那么在其不動(dòng)點(diǎn)(x0,y0)處存在關(guān)于x,y的偏導(dǎo)數(shù),，而且關(guān)于x,y的偏導(dǎo)數(shù)之和：|f′x(x0,y0)|+|f′y(x0,y0)|與|g′x(x0,y0)|+|g′y(x0,y0)|不能同時(shí)小于1,。

　　結(jié)論2動(dòng)力系統(tǒng)如式（1），如果二元函數(shù)f(x,y)與g(x,y)定義域?yàn)椋?,1］×［0,1］,，值域是［0,1］，在定義域內(nèi)存在關(guān)于x,y的偏導(dǎo)數(shù),。f(x,y)與g(x,y)構(gòu)成動(dòng)力系統(tǒng),，如果在這個(gè)動(dòng)力系統(tǒng)的兩個(gè)周期點(diǎn)(x0,y0)與(x1,y1)處關(guān)于x,y的偏導(dǎo)數(shù)滿足條件： |f′x(x0,y0)|+|f′y(x0,y0)|<1,|g′x(x0,y0)|+|g′y(x0,y0)|<1，|f′x(x1,y1)|+|f′y(x1,y1)|<1,|g′x(x1,y1)|+|g′y(x1,y1)|<1,，那么該動(dòng)力系統(tǒng)不是混沌的,。

　　結(jié)論3二元連續(xù)可導(dǎo)函數(shù)構(gòu)成動(dòng)力系統(tǒng)如式（1）所示，如果對于N周期中的N個(gè)點(diǎn)（N為正整數(shù)）,，都滿足式（9）：

　　那么該動(dòng)力系統(tǒng)不是混沌的,。與Lyapunov指數(shù)相比，這種判斷條件雖然不是充分條件,，但是也能夠排除諸多的非混沌系統(tǒng),，準(zhǔn)確地驗(yàn)證一個(gè)系統(tǒng)是否是遍歷混沌的。另外這種方法不需要計(jì)算特征值,，不需要取對數(shù),，可以節(jié)省時(shí)間。

　　上面討論的都是二維函數(shù)構(gòu)成的動(dòng)力系統(tǒng),，三維函數(shù)構(gòu)成的動(dòng)力系統(tǒng)也存在著類似于結(jié)論1和結(jié)論2的結(jié)果,。

2多個(gè)動(dòng)力系統(tǒng)構(gòu)成非線性函數(shù)迭代系統(tǒng)

　　在第1節(jié)中研究的是二維函數(shù)構(gòu)成動(dòng)力系統(tǒng)的情形，下面將多個(gè)三維函數(shù)構(gòu)成的動(dòng)力系統(tǒng)組合在一起,，構(gòu)成隨機(jī)非線性迭代系統(tǒng),，按照一定的概率，隨機(jī)選取其中的某個(gè)動(dòng)力系統(tǒng)進(jìn)行迭代,，這樣,，可以生成更多形式的更加復(fù)雜多樣的吸引子圖形,。例如使用式(10)所示的動(dòng)力系統(tǒng)構(gòu)造隨機(jī)非線性迭代系統(tǒng)：

　　使用4個(gè)如式（10）所示的動(dòng)力系統(tǒng)組成一個(gè)迭代系統(tǒng)，當(dāng)f(x,y,z)參數(shù)k分別取1.5,、2,、2.5、3,，g(x,y,z)的系數(shù)如表1所示,，h(x,y,z)的系數(shù)如表2所示，這時(shí)繪制出的吸引子圖形如圖5所示,。

　　使用4個(gè)如式（10）所示的動(dòng)力系統(tǒng)組成一個(gè)迭代系統(tǒng),，當(dāng)f(x,y,z)參數(shù)k分別取1.5, 2, 2.5, 3；g(x,y,z)的系數(shù)如表3所示,；h(x,y,z)的系數(shù)如表4所示,，這時(shí)繪制出的吸引子圖形如圖6所示。 

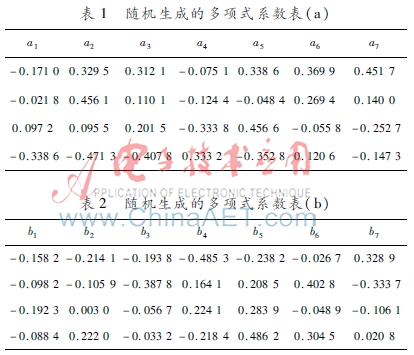
　　圖6根據(jù)表3和表4系數(shù)繪制出的吸引子

3結(jié)論

　　本文給出了一種實(shí)用的混沌吸引子生成方法,，利用正弦函數(shù)等混沌性質(zhì)較好的函數(shù)與隨機(jī)多項(xiàng)式函數(shù)構(gòu)成動(dòng)力系統(tǒng)進(jìn)行迭代,，可產(chǎn)生大量的具有觀賞和使用價(jià)值的吸引子。圖案幾乎不可以窮盡,，變化多端,，有很多具有相當(dāng)高的審美價(jià)值與研究價(jià)值。

　　使用少數(shù)的方程構(gòu)成線性IFS迭代可以生成樹,、山等自然景物,，使用非線性方程組進(jìn)行迭代能否很容易地生成動(dòng)物與人，這是一個(gè)需要進(jìn)一步研究的工作,。

參考文獻(xiàn)

　?。?］ DUMITRU D, LOANA L, SFETCU R C, et al．Topological version of generalized (infinite) iterated function systems［J］ ．Chaos,Solitons & Fractals, 2015(71):7890.

　　［2］ AVERBECK N, RAINES B E. Distributional chaos in dendritic and circular Julia sets［J］ ．Journal of Mathematical Analysis and Applications,2015,8(15): 951958.

　?。?］ Barnsley M F, HARRINGTON A N. A mandelbrot set for pairs of linear maps［J］.Physica D: Nonlinear Phenomena, 1985,4(3):421432.

　?。?］ Li Chunbiao, SPROTT J C, THIO W．Linearization of the Lorenz system［J］.Physics Letters A, 2015, 5(10):888893.

　　［5］ Zhou Changsong, Chen Tianlun. Chaotic neural networks and Chaotic annealing［J］. Neurocomputing, 2000,30(14):293300.

　?。?］ 秦元?jiǎng)?曾憲武．生物化學(xué)中的布魯塞爾振子方程的定性研究［J］.科學(xué)通報(bào),， 1980(8)：337339.

　　［7］ 于萬波,，周洋．空間單位區(qū)域雙二次有理貝賽爾曲面混沌特性研究［J］ ．物理學(xué)報(bào),，2013（22）： 2535.

　　［8］ 于萬波,，趙斌．曲面迭代混沌特性研究［J］.物理學(xué)報(bào),，2014（12）：3141.

　　［9］ 于萬波．截面的幾何形狀決定三維函數(shù)的混沌特性［J］ ．物理學(xué)報(bào),，2014（12）：2230.