(1.廣西大學 計算機與電子信息學院,，廣西 南寧 530004,；2.浙江海洋學院 數(shù)理與信息學院，浙江 舟山 316000)

　　摘要：標準的量子遺傳算法容易陷入局部最優(yōu),，且在定義域范圍較廣的函數(shù)尋優(yōu)中易出現(xiàn)優(yōu)化精度不高的情況,。將量子交叉與模擬退火操作適當?shù)丶尤肓孔舆z傳算法中可以有效地避免算法陷入局部最優(yōu)解。根據(jù)第一次的優(yōu)化結(jié)果,，縮小算法尋優(yōu)區(qū)域,，以提高算法尋優(yōu)的精確度。最后對其用復雜二元函數(shù)進行測試,，計算結(jié)果表明,，通過該改進方式明顯提高了優(yōu)化算法的性能。

　　關鍵詞：量子遺傳算法,；量子交叉,；退火操作；尋優(yōu)區(qū)域

0引言

　　量子遺傳算法［1］（Quantum Genetic Algorithm,，QGA）是將經(jīng)典量子計算與傳統(tǒng)遺傳算法的操作方式相互融合產(chǎn)生的新的優(yōu)化算法,。與傳統(tǒng)遺傳算法相比，量子遺傳算法具有種群多樣性好,、全局搜索能力強和收斂速度快等特點［2］,。

　　標準的量子遺傳算法在一些特別復雜的、病態(tài)的優(yōu)化函數(shù)中不能充分地發(fā)揮其優(yōu)越的性能,。為了提高算法的優(yōu)化性能,，本文將模擬退火操作與量子交叉操作引入標準量子遺傳算法中。該算法在量子個體上實施量子交叉操作,，增強種群中染色體的結(jié)構(gòu)信息交流,，引入退火思想盡量避免算法在早期時陷入局部極值［3］。在實施第一輪尋優(yōu)計算操作后,，求出相應的最優(yōu)解,，再在最優(yōu)解附近的小范圍內(nèi)進行第二輪尋優(yōu)計算,，提高算法的尋優(yōu)精確度。

　　針對改進后的量子遺傳算法,，本文用幾個復雜二元函數(shù)進行測試,，結(jié)果表明，改進后的算法具有較強全局搜索［4］的特點,。

1量子遺傳算法

　　1.1量子編碼

　　量子遺傳算法的編碼方式是量子編碼。量子編碼中,，信息的存儲單元是量子比特［5］,。采用|0>和|1>的單量子比特的疊加態(tài)來表示遺傳信息。

　　在量子遺傳算法中的量子位可以是|0>到|1>中的任意值,，所以一個量子位的狀態(tài)的表達式可以為［6］：

　　|ρ>=λ|0>+μ|1>(1)

　　其中量子態(tài)的概率幅λ與μ是一對平方和為1的復數(shù),。對優(yōu)化種群進行一次測量操作，|ρ>可能會以|λ|2的概率坍縮到| 0>狀態(tài),，或者會以|μ|2的概率坍縮到|1>的狀態(tài),，并且它們滿足下面的表達式條件：

　　|α|2+|β|2=1(2)

　　在式(2)中，|α|2表示|0>的概率,，|β|2表示|1>的概率,，量子態(tài)坍縮是為了結(jié)合適應度值來優(yōu)選種源。因此,，如果一個系統(tǒng)有m個量子位,，則該系統(tǒng)可同時描述2m個狀態(tài)。然而,，對于量子態(tài)［4］的每一次觀察,，該量子位都只會坍縮到一個確定的狀態(tài)。

　　1.2染色體表示方法

　　在量子遺傳算法中,，基因采用量子比特來表示［5］,。該基因可以是“0”態(tài)或“1”態(tài)，也可以是它們之間的任意疊加態(tài),，即每一個基因位代表的不再是某一確定的遺傳信息,，而是包含該優(yōu)化函數(shù)所需要的所有的優(yōu)化解集信息。因此,，對于任意基因位的任一操作都可能會使種群中所有的優(yōu)化解集信息產(chǎn)生變化,。本文使用一對平方和為1的復數(shù)對(α,β)來表示染色體中的一個量子比特，則 c個j位基因構(gòu)成的一個染色體可以表示為：

　　式中,，i是染色體的編號,，n是染色體當前進化的代數(shù)，c是基因位的個數(shù),，第n代第i個個體的染色體用qni描述,；j是每個用二進制表示的優(yōu)化解中含有的量子比特數(shù),。

2量子遺傳算法的改進

　　2.1量子交叉

　　在標準的量子遺傳算法中，沒有量子交叉,，種群中染色體都相互獨立,，個體間的結(jié)構(gòu)信息不能被充分利用。

　　參考文獻［7］采用一種叫做“全局干擾交叉”的交叉操作,，在該交叉操作中所有的染色體都參與其中,。表1簡單地描述了本文中量子交叉方式，即該種群的大小為3,，染色體的個數(shù)為3,，每個染色體的長度為5。

　　其中第二個染色體的第2個量子比特用B（2）來表示,，用遞歸的方式來進行全局干擾操作,。交叉后的染色體的基因位的確定方法是：交叉前的基因位以現(xiàn)在的基因位序號大小減1在種群中向下移動幾位，如果移動的位數(shù)超過種群染色體數(shù)則除以現(xiàn)在種群的大小,，然后取得的余數(shù)減1就是該基因向下移動的位數(shù),。

　　表2所示是經(jīng)過全局干擾交叉操作后的染色體組，如：B（1）—A（2）—C（3）—B（4）—A（5）,。通過此類操作,，優(yōu)化種群中每個染色體上的量子位信息將會被充分利用，在種群演化的后期能夠充分保證染色體的多樣性,，提高了算法的性能,。

　　2.2模擬退火操作

　　模擬退火操作是通過設置初始溫度的大小與現(xiàn)實降溫過程的速率來實現(xiàn)的。在溫度較高時,，算法能夠以較高的概率接受差的優(yōu)化解,，而溫度較低時能較好地接受好的優(yōu)化解，通過此操作使算法避免陷入局部極值,。模擬退火的搜索模式提高了算法的搜索能力和效率,。

　　模擬退火算法實際上是一種迭代求解的過程，算法反復執(zhí)行“產(chǎn)生新狀態(tài)計算目標函數(shù)判斷是否接受新狀態(tài)接受/舍棄”的過程,。它的基本流程如下：

　　(1)初始化,，初始溫度T，初始解S,，每個T值的迭代次數(shù),。

　　（2）對種群完成步驟（3）~（6）,。

　?。?）產(chǎn)生新的解S′。

　?。?）計算增量Δ=E(S′)－E(S),其中E(S)為目標函數(shù),。

　?。?）若Δ<0，則接受S′作為新的當前解,，否則以概率exp(－Δ/T)接受S′為新的當前解,。

　　（6）如果滿足終止條件則輸出當前解作為最優(yōu)解,，結(jié)束循環(huán),。

　　（7）產(chǎn)生新的溫度T′=0.95×T,，逐步降低T（溫度）,。

　　（8）轉(zhuǎn)到步驟（2）,。

　　在算法的執(zhí)行過程中，為了保證算法的收斂能力,，要保證退火的初始溫度T盡可能的大,，一般情況下T取值為100。

　　2.3二次尋優(yōu)計算

　　2.3.1粗格子點法

　　粗格子點法是先用少數(shù)的格子點進行粗糙計算,，在求出相應的最優(yōu)解后,，再在最優(yōu)解附近的小范圍內(nèi)進一步細分，并求在細分格子點上的最優(yōu)解,，如此繼續(xù)細分直到滿足要求為止,。

　　2.3.2二次尋優(yōu)計算方式

　　二次尋優(yōu)計算方式與粗格子點法相似。二次尋優(yōu)計算是第一次尋優(yōu)計算后在得到的最優(yōu)解附近的小范圍內(nèi)再利用量子遺傳算法進行尋優(yōu)計算操作,。優(yōu)點在于優(yōu)化函數(shù)定義域縮小,，最優(yōu)值所在的區(qū)域更加明顯，染色體解的精度更高,。

　　2.3.3二次尋優(yōu)計算區(qū)域

　　二次尋優(yōu)計算區(qū)域為第一次尋優(yōu)計算時每代的最優(yōu)值解組成的連續(xù)區(qū)域集合,。如下圖1所示，以第一次尋優(yōu)計算的全局最優(yōu)解A為中心點,，以中心點到邊界點B的距離為長度,，確定該方向上二次尋優(yōu)計算的區(qū)間。

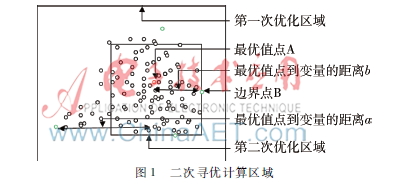
　　在圖1中,，如果a<b,則將該方向上二次尋優(yōu)計算區(qū)域的二分之一大小設置為a,否則,，設置為b。同理確定各個方向上變量的二次尋優(yōu)計算的區(qū)域大小,。該方式縮小了算法二次尋優(yōu)計算的區(qū)域,，提高了算法尋優(yōu)精確度。

　　2.4改進算法選擇

　　每個改進的量子遺傳算法都具有不同的尋優(yōu)計算特性,。如果在第一次優(yōu)化計算函數(shù)時,，發(fā)現(xiàn)全局最優(yōu)解的出現(xiàn)代數(shù)較小,，且尋優(yōu)效果不佳，多數(shù)情況是由于算法的“早熟收斂”造成的,。因此,，在下次的尋優(yōu)計算時，可以將退火操作引入算法中,，防止算法的“早熟收斂”,。如果出現(xiàn)最優(yōu)解的迭代次數(shù)較晚，且尋優(yōu)效果較差,，多數(shù)情況是由于各染色體過于孤立,，染色體結(jié)構(gòu)信息交流少，收斂速度慢造成的,。因此,，在下次尋優(yōu)計算時，將量子交叉操作引入優(yōu)化算法中,，增加種群的多樣性,，提高算法的尋優(yōu)性能。使用二次尋優(yōu)計算,，可以有效地提高算法尋優(yōu)的精度,。

　　2.5優(yōu)化算法流程

　　改進量子遺傳算法（IQGA）流程主要分為以下步驟：

　　（1）對初始種群Q（t0）進行函數(shù)優(yōu)化解集種群的初始化操作,初始溫度T,，(αij,βij)描述的是所有優(yōu)化解集種群中每個染色體上的一個基因位,，(2/2,2/2)是它們的初始大小。

　?。?）對初始種群中的每個個體進行一次測量,，得到對應確定的解P(t0)。

　?。?）對各確定染色體優(yōu)化解P(t0)進行適應度評估操作,，以此來得到每個解的適應度值的大小，用來進行下一步的遺傳淘汰選擇操作,。

　?。?）記錄最優(yōu)個體和對應的適應度。

　?。?）判斷優(yōu)化算法是否可以結(jié)束優(yōu)化操作,，如果現(xiàn)有的優(yōu)化解集滿足優(yōu)化結(jié)束的條件則執(zhí)行步驟（12），否則繼續(xù)執(zhí)行優(yōu)化操作,。

　?。?）對優(yōu)化解集種群Q(t)中的每個個體即染色體優(yōu)化解進行一次染色體基因位大小的確定操作，通過此操作得到對應遺傳代數(shù)種群的函數(shù)優(yōu)化解集。

　?。?）對各確定解進行適應度評估,。

　　（8）利用量子旋轉(zhuǎn)門U(t)對每個染色體個體進行一次遺傳演化操作,，若當代全局適應度值與前代適應度值之差Δ小于零,，則接受當代最優(yōu)個體作為新的當前解，以此得到新的優(yōu)化函數(shù)的最優(yōu)解集種群Q(t+1),，否則以概率exp(－Δ/T)接受新的當前解,，以此得到新的優(yōu)化函數(shù)的最優(yōu)解集種群Q(t+1)。

　?。?）對量子染色體進行全干擾的量子交叉操作,。

　　（10）記錄最優(yōu)個體和對應的適應度,。

　?。?1）將迭代次數(shù)t加1，返回步驟(5),。

　?。?2）確定二次優(yōu)化解集區(qū)域，并將算法迭代次數(shù)減半,，修正退火系數(shù),。

　?。?3）根據(jù)第一次優(yōu)化方法,，執(zhí)行步驟（1）~（11）。

3算法性能測試

　　3.1典型測試函數(shù)

　?。?）多峰函數(shù)Shubert［8］

　　f1(x1,x2)=min∑5i=1icos［(i+1)x1+i］·

　　∑5i=1icos［(i+1)x2+i］

　　此函數(shù)具有760個局部極小值,，其中全局最小值18個，理論上的全局最小解fmin(x1,x2)=－186.731,。

　?。?）Goldsten-Price函數(shù)［9］

　　f2(x1,x2)=［1+(x1+x2+1)2(19－14x1+3x21－14x2+6x1x2+3x22)］*［30+(2x1－3x2)2(18－32x1+12x21+48x2-36x1x2+27x22)］，-2≤x1,x2≤2

　　此函數(shù)在其定義域內(nèi)只有一個極小值點f2(0,－1)=3,。

　?。?）Sixhump Camel Back函數(shù)

　　f3(x,y)=(4－2.1x2+x4/3)x2+xy+(－4+4y2)y2，-3≤x≤3,，－2≤y≤2

　　Sixhump Camel Back函數(shù)有多個相似極小值點,，很難準確地取得最小值點，其中(-0.089 8,，0.712 6)和(0.089 8,，-0.712 6)為全局最小點，最小值為f3(－0.089 8,0.712 6)=－1.031 628和f3(0.089 8,－0.712 6)=－1.031 628。

　　本文采用的方法與現(xiàn)有方法的計算結(jié)果對比如表3所示,，每個函數(shù)分別用改進后的算法計算20次,。量子遺傳算法的種群大小設置為40，迭代次數(shù)設置為200,，函數(shù)的每個變量的二進制長度設置為20,，退火初始溫度設置為100℃，退火系數(shù)為0.95,。算法的優(yōu)化性能從算法的效率與算法質(zhì)量兩個方面進行評價,。

　　注：QGA為基本量子遺傳算法；CQGA為含量子交叉的算法,；SQGA為含退火操作的算法,；SCQGA為基于量子交叉與退火操作的算法

　　根據(jù)表3數(shù)據(jù)可以看出，改進后的量子遺傳算法在性能上有了一定的提高,。針對不同的優(yōu)化函數(shù),，改進算法都體現(xiàn)了其優(yōu)越的性能。含量子交叉與退火思想的量子遺傳算法對于不同特點的優(yōu)化函數(shù)都能保持較好的搜索能力,。

　　3.2二次尋優(yōu)計算測試

　　為測試二次尋優(yōu)計算的性能,，利用上文提及的3個典型函數(shù)進行性能測試。將最大遺傳代數(shù)設置為100,，染色體長度為20,，種群大小為40。計算結(jié)果和對照比較內(nèi)容如表4所示,。 

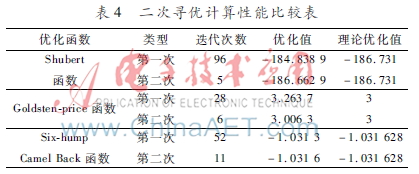
　　從表4可以看出,，二次尋優(yōu)計算得到的全局最優(yōu)值比第一次得到的解更加接近理論最優(yōu)值，并且收斂速度更快,。

　　4結(jié)論

　　本文通過在原有的量子遺傳中添加全干擾的量子交叉與退火操作,，提高了量子遺傳算法的搜索尋優(yōu)能力，有效地避免傳統(tǒng)算法易陷入“早熟收斂”與局部極值的問題,。本文使用的二次尋優(yōu)計算提高了算法的精確度,。

　　但是，本文的研究還有很多需要改進的地方,，比如,，在二次優(yōu)化時優(yōu)化區(qū)域的確定過于單一，沒有加入權(quán)值,，可以考慮在優(yōu)化時對每代的最優(yōu)值賦權(quán)值,，根據(jù)權(quán)值來確定二次優(yōu)化的尋優(yōu)區(qū)域；可以將全局交叉設置為概率交叉,，在不影響性能的情況下減少交叉次數(shù),；可以使用并行算法縮減含量子交叉操作的量子遺傳算法的運行時間。因此，本文的后續(xù)工作是在現(xiàn)有基礎上改進和完善優(yōu)化算法,，使其能更好地進行函數(shù)尋優(yōu),。

參考文獻

　　［1］ 梁昌勇,，柏樺,，蔡美菊，等.量子遺傳算法研究進展［J］.計算機應用研究,，2012,29（7）：24012405.［2］ 周傳華,，錢鋒.改進量子遺傳算法及其應用［J］.計算機應用，2008,28(2)：286288.

　?。?］ 郭海燕,，金煒東，李麗,，等．分組量子遺傳算法及其應用［J］．西南科技大學學報,，2004，19(1)：1821.

　?。?］ 何兵.基于改進量子遺傳算法的巡航導彈水平航跡規(guī)劃［J］.計算機仿真,，2012,29(9):109112.

　　［5］ 張濟濤,，樊靜波,，高亮．基于量子遺傳算法的拆除序列規(guī)劃［J］．現(xiàn)代制造工程，2015(4)：110115.

　?。?］ HAN K H. Genetic quantum algorithm and its application to combinatorial optimization problem［C］. In: IEEE Proc. of the 2000 Congress on Evolutionary Computation, San Diego, USA, 2000:13541360.

　?。?］ 祁正萍，孫合鳴．一種改進的量子遺傳算法［J］．科學技術與工程,，2012,，12(12)：28352839.

　?。?］ 席紅雷．自適應梯度小環(huán)境混合優(yōu)化算法［J］．計算機與數(shù)字工程,，2012,40(2):3739.

　　［9］ 李敏強,，寇紀淞．遺傳算法的基本理論與應用［M］．北京：科學出版社,，2002.