文獻(xiàn)標(biāo)識(shí)碼: A
DOI:10.16157/j.issn.0258-7998.181492
中文引用格式: 趙輝,周杰,王紅君,等. 基于CEEMDAN-PE和QGA-BP的短期風(fēng)速預(yù)測(cè)[J].電子技術(shù)應(yīng)用,2018,44(12):60-64.
英文引用格式: Zhao Hui,Zhou Jie,Wang Hongjun,et al. Short-term wind speed prediction based on CEEMDAN-PE and QGA-BP[J]. Application of Electronic Technique,2018,44(12):60-64.
0 引言
風(fēng)能是清潔、無污染的可再生能源,對(duì)風(fēng)能的開發(fā)和利用越來越受到重視[1]。風(fēng)存在隨機(jī)性、間歇性、不可控性的特點(diǎn),使得風(fēng)電大規(guī)模并網(wǎng)后對(duì)電力系統(tǒng)的調(diào)度、穩(wěn)定性造成嚴(yán)重影響[2],而對(duì)風(fēng)速的準(zhǔn)確預(yù)測(cè)是解決風(fēng)電并網(wǎng)問題、保證電力系統(tǒng)穩(wěn)定性的基礎(chǔ)性工作[3-4]。
近年來,尋找穩(wěn)定、精確的風(fēng)速預(yù)測(cè)模型一直是國(guó)內(nèi)外研究者關(guān)注的焦點(diǎn)。由于風(fēng)速時(shí)間序列具有明顯的隨機(jī)波動(dòng)性[5],僅僅采用單一的預(yù)測(cè)方法或尚未考慮風(fēng)速序列非平穩(wěn)性變化特征的組合預(yù)測(cè)方法往往存在預(yù)測(cè)精度不高、預(yù)測(cè)誤差較大的問題。文獻(xiàn)[6]建立了遺傳算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的預(yù)測(cè)模型,預(yù)測(cè)精度雖然比單純BP模型有所提高,但遺傳算法容易陷入局部極小值且收斂性差影響預(yù)測(cè)效果;文獻(xiàn)[7]建立了多種群遺傳算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的超短期風(fēng)速預(yù)測(cè)模型,該模型提高了預(yù)測(cè)精度,減少了運(yùn)算時(shí)間,但是未考慮原始時(shí)間序列尚未處理對(duì)預(yù)測(cè)精度的影響;文獻(xiàn)[8]和[9]用EMD和EEMD的組合模型對(duì)原始風(fēng)速時(shí)間序列進(jìn)行分解,降低了風(fēng)速序列非平穩(wěn)性對(duì)預(yù)測(cè)精度的影響,得到了較好的預(yù)測(cè)效果,但忽略了其存在的模態(tài)混疊現(xiàn)象和由于減小重構(gòu)誤差而出現(xiàn)的計(jì)算規(guī)模大和效率低的問題。當(dāng)前,CEEMDAN[10]在處理非線性、非平穩(wěn)信號(hào)方面被廣泛地應(yīng)用,該方法同時(shí)克服了EMD模態(tài)混疊問題[11]以及EEMD[12]所出現(xiàn)的計(jì)算規(guī)模和效率低下的問題,在分解風(fēng)速序列上有更好效果,具有更大的優(yōu)越性。
而量子遺傳算法[13](Quantum Genetic Algorithm,QGA)作為一種新型的概率進(jìn)化算法,它是在傳統(tǒng)遺傳算法的基礎(chǔ)上引入量子計(jì)算理論。該算法將染色體的編碼用量子比特的幾率幅來表示,從而使得多個(gè)態(tài)的疊加可以由一條染色體來表達(dá)。同時(shí)采用量子旋轉(zhuǎn)門等操作對(duì)染色體的更新進(jìn)行實(shí)現(xiàn),達(dá)到了目標(biāo)的優(yōu)化求解。該算法在種群規(guī)模小的情況下不影響算法性能,表現(xiàn)出明顯的種群多樣性和更好的收斂特性。
鑒于此,考慮到組合預(yù)測(cè)模型在短期風(fēng)速方面的優(yōu)勢(shì),本文提出一種基于CEEMDAN-PE-QGA-BP的預(yù)測(cè)模型。由于該預(yù)測(cè)模型在風(fēng)速預(yù)測(cè)領(lǐng)域研究較少,現(xiàn)進(jìn)行預(yù)測(cè)研究。最后,通過風(fēng)電場(chǎng)的實(shí)測(cè)數(shù)據(jù)進(jìn)行仿真分析驗(yàn)證了本文方法的有效性。
1 預(yù)測(cè)原理分析
1.1 相關(guān)分析法
本文利用自相關(guān)系數(shù)[14]來描述風(fēng)速時(shí)間序列不同時(shí)刻數(shù)據(jù)點(diǎn)的相關(guān)程度,通過比較自相關(guān)系數(shù)ρ的大小來判斷相關(guān)程度的強(qiáng)弱。定義延時(shí)為k的自相關(guān)系數(shù)為:

式中,E為期望,xt為時(shí)間序列,ux為序列平均值,Cov為協(xié)方差,σ為方差。可以通過設(shè)置不同的延時(shí)k研究時(shí)間序列的自相關(guān)性,為時(shí)間序列構(gòu)建預(yù)測(cè)模型做準(zhǔn)備。當(dāng)相關(guān)系數(shù)ρk≥0.90時(shí),表明相鄰時(shí)刻的相關(guān)性最高。
1.2 CEEMDAN算法
與EEMD算法相比,CEEMDAN在原始信號(hào)X[n]中添加滿足標(biāo)準(zhǔn)正態(tài)分布的高斯白噪聲ω[n],則第i次的信號(hào)可以表示為Xi[n]=X[n]+ωi[n](i=1,…,I),其中I為實(shí)驗(yàn)次數(shù),CEEMDAN的分解過程如下:

1.3 排列熵
排列熵(Permutation Entropy,PE)反映了一維時(shí)間序列復(fù)雜度,其計(jì)算簡(jiǎn)單,能夠較好地放大時(shí)間序列數(shù)據(jù)的微小變化[15],對(duì)時(shí)間序列的變化具有很高的敏感性。PE的具體計(jì)算過程如下:
對(duì)時(shí)間序列{x(i),i=1,2,…,N}進(jìn)行相空間重構(gòu)后得到重構(gòu)向量:

顯然,Hp的取值范圍為0≤Hp≤1,Hp值的大小反映了時(shí)間序列的隨機(jī)性程度。Hp越大,說明時(shí)間序列的隨機(jī)性越強(qiáng);Hp越小,說明時(shí)間序列越規(guī)則。
1.4 BP神經(jīng)網(wǎng)絡(luò)
BP神經(jīng)網(wǎng)絡(luò)是當(dāng)前應(yīng)用最廣泛的神經(jīng)網(wǎng)絡(luò),其主要特點(diǎn)是信號(hào)前向傳遞、誤差反向傳播。BP神經(jīng)網(wǎng)絡(luò)的具體過程詳見文獻(xiàn)[16]。
2 QGA優(yōu)化BP算法設(shè)計(jì)
本文采用QGA算法對(duì)權(quán)值和閾值參數(shù)進(jìn)行優(yōu)化。量子遺傳算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的流程圖如圖1所示。

3 基于CEEMDAN-PE-QGA-BP短期風(fēng)速預(yù)測(cè)模型
綜合CEEMDAN和PE的優(yōu)點(diǎn),結(jié)合量子遺傳優(yōu)化BP神經(jīng)網(wǎng)絡(luò)建立預(yù)測(cè)模型,該模型框架如圖2所示。

4 仿真分析
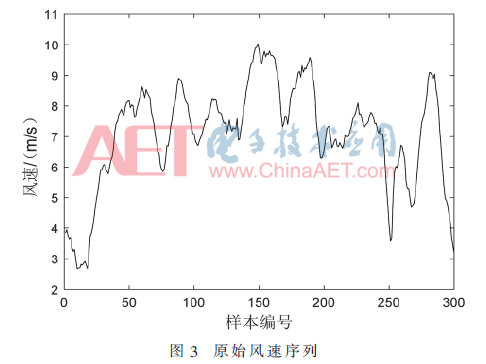
為了檢驗(yàn)本文所建模型的合理性,采用江蘇某風(fēng)電場(chǎng)在2013年12月1~4日中實(shí)測(cè)的300個(gè)風(fēng)速數(shù)據(jù)值為樣本進(jìn)行試驗(yàn)仿真。圖3為原始風(fēng)速序列。
利用相關(guān)分析法計(jì)算時(shí)間序列的自相關(guān)系數(shù)ρ,以確定模型的輸入變量。自相關(guān)系數(shù)如表1所示,前5個(gè)時(shí)刻的風(fēng)速值相關(guān)系數(shù)在0.9以上,風(fēng)速的相關(guān)性最高,即輸入變量個(gè)數(shù)選取為5。認(rèn)為前5個(gè)時(shí)刻的風(fēng)速值對(duì)預(yù)測(cè)時(shí)刻的風(fēng)速值影響很大。根據(jù)此將每6個(gè)數(shù)據(jù)分為一組,前5個(gè)風(fēng)速值作為輸入,第6個(gè)作為輸出進(jìn)行依次循環(huán)預(yù)測(cè)。因此,采集的300個(gè)風(fēng)速數(shù)據(jù)樣本轉(zhuǎn)換后共295組,其中將235組作為訓(xùn)練數(shù)據(jù),60組作為測(cè)試數(shù)據(jù),在MATLAB平臺(tái)上進(jìn)行仿真預(yù)測(cè)。

4.1 數(shù)據(jù)處理
采用CEEMDAN分解方法對(duì)原始風(fēng)速序列進(jìn)行分解。風(fēng)速序列被分解為7個(gè)波動(dòng)較小的IMF分量和一個(gè)剩余分量r8。分解結(jié)果如圖4所示。

對(duì)每一IMF分量分別計(jì)算PE值。由于嵌入維數(shù)m對(duì)時(shí)間序列的計(jì)算影響較大,一般建議嵌入維數(shù)m取3~7。因此,在實(shí)際考慮本文的分解結(jié)果,選取m=3,而時(shí)延τ對(duì)時(shí)間序列的計(jì)算影響較小,通常取1即可。當(dāng)m=3、τ=1時(shí),PE的計(jì)算結(jié)果如圖5所示。
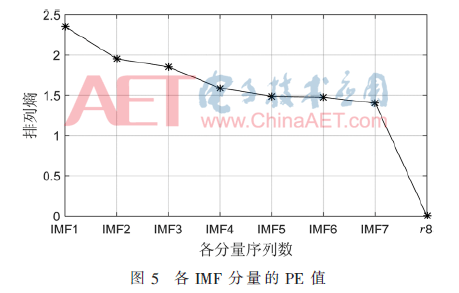
從圖5可以看出,各IMF分量的PE值隨著IMF頻率的降低而逐漸遞減,這說明分量從IMF1到r8序列越來越規(guī)則。根據(jù)計(jì)算出熵值的相似性及接近程度這一原則對(duì)各個(gè)分量進(jìn)行重組。在圖5中顯示出,IMF1分量的PE值最大、隨機(jī)性最強(qiáng),熵值明顯高于其他分量;IMF2和IMF3呈現(xiàn)出一定的隨機(jī)性,PE值一定程度上較為接近,可以合并;IMF4~I(xiàn)MF7表現(xiàn)出明顯的相似性且PE值差異非常接近,也可將其進(jìn)行合并;而趨勢(shì)項(xiàng)分量r8為平穩(wěn)分量,其PE值為0,可以將其單獨(dú)為一個(gè)新的序列。具體的重組情況如表2所示。

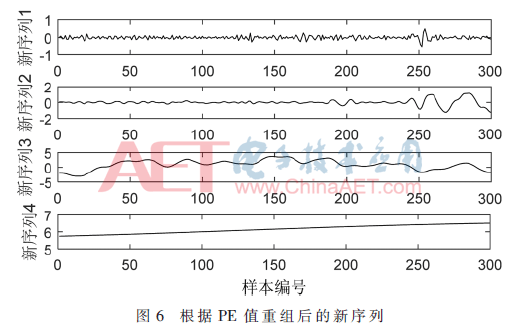
根據(jù)表2中重組的結(jié)果,得到疊加后新的序列如圖6所示。
4.2 QGA-BP預(yù)測(cè)
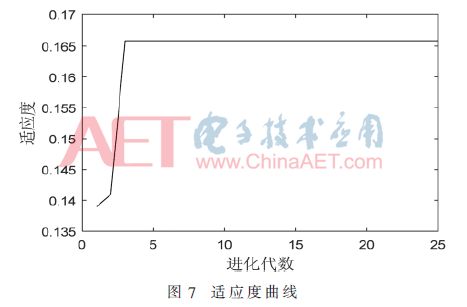
在對(duì)數(shù)據(jù)進(jìn)行處理后,根據(jù)前面所建的預(yù)測(cè)模型在MATLAB平臺(tái)上進(jìn)行仿真預(yù)測(cè)。BP神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)為輸入層、隱含層、輸出層。神經(jīng)元個(gè)數(shù)分別為5、11、1。設(shè)定網(wǎng)絡(luò)訓(xùn)練的最大迭代次數(shù)為1 000,學(xué)習(xí)率為0.005,誤差為10-20。QGA的種群規(guī)模為20,最大進(jìn)化代數(shù)取25。將實(shí)際輸出與期望輸出之間誤差和的倒數(shù)作為適應(yīng)度函數(shù),誤差越小,適應(yīng)度越大。QGA適應(yīng)度圖如圖7所示。
根據(jù)建立好的預(yù)測(cè)模型,利用測(cè)試數(shù)據(jù)對(duì)其進(jìn)行預(yù)測(cè),實(shí)際風(fēng)速與本文預(yù)測(cè)模型預(yù)測(cè)的風(fēng)速對(duì)比如圖8所示。

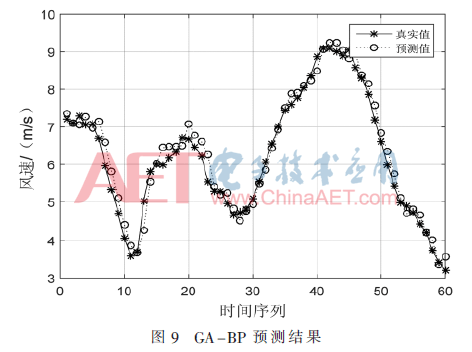
為了驗(yàn)證本文提出預(yù)測(cè)模型具有更好的預(yù)測(cè)效果,在相同的網(wǎng)絡(luò)結(jié)構(gòu)和測(cè)試樣本環(huán)境下,與遺傳算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)模型(GA-BP)和LSSVM預(yù)測(cè)模型的預(yù)測(cè)結(jié)果進(jìn)行對(duì)比。GA-BP預(yù)測(cè)結(jié)果和LSSVM的預(yù)測(cè)結(jié)果分別如圖9和圖10所示。

4.3 預(yù)測(cè)結(jié)果分析
從圖8~圖10中可以直觀地看出,圖8的預(yù)測(cè)值和真實(shí)值最接近,效果最優(yōu);GA-BP模型次之,LSSVM模型最差。表明本文提出的預(yù)測(cè)模型相對(duì)于另外2種預(yù)測(cè)模型更適于進(jìn)行短期風(fēng)速預(yù)測(cè)。
為了進(jìn)一步更好地比較3種預(yù)測(cè)模型的性能,采用均方誤差MSE和決定系數(shù)R2作為預(yù)測(cè)模型性能的檢驗(yàn)指標(biāo)。均方誤差越小、決定系數(shù)越大,則模型的預(yù)測(cè)效果越好。具體計(jì)算公式如下:

表3列出了經(jīng)過檢驗(yàn)指標(biāo)計(jì)算后3種模型預(yù)測(cè)性能對(duì)比結(jié)果。可以看出,與GA-BP和LSSVM模型相比,本文提出的方法誤差最小。傳統(tǒng)的GA-BP模型雖然避免單一BP模型出現(xiàn)易陷入局部極值的情況,但是本身過于繁雜,誤差較大。而本文的組合模型同樣也避免了陷入局部最優(yōu)的缺陷,并且在預(yù)測(cè)精度和誤差減小方面有很大提高。對(duì)比的結(jié)果表明,在短期風(fēng)速預(yù)測(cè)方面,用GA-BP預(yù)測(cè)模型雖然有一定的效果,而采用本文預(yù)測(cè)模型的預(yù)測(cè)效果更好、更準(zhǔn)確,表現(xiàn)出了明顯的優(yōu)勢(shì)。

5 結(jié)束語
本文通過建立CEEMDAN-PE-QGA-BP模型對(duì)江蘇某風(fēng)電場(chǎng)風(fēng)速進(jìn)行預(yù)測(cè),并將預(yù)測(cè)結(jié)果與GA-BP 模型、LSSVM模型的預(yù)測(cè)結(jié)果進(jìn)行對(duì)比。仿真結(jié)果表明,采用CEEMDAN-PE對(duì)原始風(fēng)速序列進(jìn)行處理,有效地降低了原始序列的非平穩(wěn)性,減小了分別對(duì)分量進(jìn)行預(yù)測(cè)的計(jì)算規(guī)模;采用QGA算法對(duì)BP算法進(jìn)行優(yōu)化,克服了BP模型在初始權(quán)值、閾值選取上存在的不足,并且相比于傳統(tǒng)遺傳算法優(yōu)化的BP神經(jīng)網(wǎng)絡(luò)模型,其能夠收斂到全局最優(yōu)解,提高了收斂特性。總體上,本文所提的組合模型提高了預(yù)測(cè)的精度,減小了預(yù)測(cè)的誤差,得到較好的預(yù)測(cè)效果,在今后風(fēng)速預(yù)測(cè)方面具有重要的意義。
參考文獻(xiàn)
[1] 張妍,韓璞,王東風(fēng),等.基于變分模態(tài)分解和LSSVM的風(fēng)電場(chǎng)短期風(fēng)速預(yù)測(cè)[J].太陽能學(xué)報(bào),2018,39(1):194-202.
[2] 葉瑞麗,郭志忠,劉瑞葉,等.基于小波包分解和改進(jìn)Elman神經(jīng)網(wǎng)絡(luò)的風(fēng)電場(chǎng)風(fēng)速和風(fēng)電功率預(yù)測(cè)[J].電工技術(shù)學(xué)報(bào),2017,32(21):103-111.
[3] 張妍,韓璞.基于CEEMD-LSSVM的風(fēng)電場(chǎng)短期風(fēng)速預(yù)測(cè)[J].計(jì)算機(jī)仿真,2017,34(8):408-411,444.
[4] 谷興凱,范高峰,王曉蓉.風(fēng)電功率預(yù)測(cè)技術(shù)綜述[J].現(xiàn)代電力,2017,31(2):335-338.
[5] 袁東鋒,杜恒.基于小波分析和相空重構(gòu)相融合的風(fēng)速預(yù)測(cè)[J].計(jì)算機(jī)仿真,2013,30(3):331-334,388.
[6] 王德明,王莉,張廣明.基于遺傳BP神經(jīng)網(wǎng)絡(luò)的短期風(fēng)速預(yù)測(cè)模型[J].浙江大學(xué)學(xué)報(bào)(工學(xué)版),2012,46(5):837-841,904.
[7] 陳忠.基于BP神經(jīng)網(wǎng)絡(luò)與遺傳算法風(fēng)電場(chǎng)超短期風(fēng)速預(yù)測(cè)優(yōu)化研究[J].可再生能源,2012,30(2):32-36.
[8] 朱亞,孫冬梅,何響,等. 基于EMD-GRNN和概率統(tǒng)計(jì)結(jié)合的短期風(fēng)速預(yù)測(cè)[J].計(jì)算機(jī)科學(xué),2014,41(S1):72-75.
[9] 何群,趙文爽,江國(guó)乾,等.基于EEMD與AR建模的風(fēng)電場(chǎng)風(fēng)速預(yù)測(cè)[J].計(jì)量學(xué)報(bào),2015(2):181-186.
[10] TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al.A.complete ensemble empirical mode decomposition with adaptive noise[C].2011 IEEE International Conference On Acoustics,Speech and Signal Processing.Piscataway, NJ,SA:IEEE,2011:4144-4147.
[11] 向丹,葛爽.基于EMD樣本熵-LLTSA的故障特征提取方法[J].航空動(dòng)力學(xué)報(bào),2014,29(7):1535-1542.
[12] ZHAOHUA W,NORDEN E H.Ensemble empirical mode decomposition:a noise-assisted data analysis method[J].Advances in Adaptive Data Analysi,2011,1(1):1-41.
[13] TOTH G,LENTC S,TOUGAW P D,et al.Quantum cellular neural networks[J].Superlattices and Microstructures,1996,20(4):473-478.
[14] 孫紅果,鄧華.樣本自相關(guān)系數(shù)與偏自相關(guān)系數(shù)的研究[J].蚌埠學(xué)院學(xué)報(bào),2016,5(1):35-39.
[15] CAO Y,TUNG W W,GAO J B,et al.Detecting dynamical changes in time series using the permutation entropy[J].Phy.Rev.E.Stat.Nonlin.Soft.Matter.Phys.,2004,70(4):174-195.
[16] 馮冬青,李衛(wèi)帥.基于GA-BP神經(jīng)網(wǎng)絡(luò)的電池剩余電量的預(yù)測(cè)[J].計(jì)算機(jī)仿真,2011(12):323-326,324.
作者信息:
趙 輝1,2,周 杰1,王紅君1,岳有軍1
(1.天津理工大學(xué) 天津市復(fù)雜系統(tǒng)控制理論與應(yīng)用重點(diǎn)實(shí)驗(yàn)室,天津300384;2.天津農(nóng)學(xué)院,天津300384)

