陳仁愛，凌強(qiáng),，徐駿,，李峰

　　(中國科學(xué)技術(shù)大學(xué) 信息科學(xué)技術(shù)學(xué)院,，安徽 合肥 230026)

 摘要：霍夫圓變換是圖像處理中人眼檢測的一種常見方法，但是其處理的數(shù)據(jù)量多,，處理速度慢,，在移植到DSP上后難以滿足實(shí)時性要求。對此,，提出了一種將兩階段霍夫圓變換算法應(yīng)用到 TMS320C6000系列 DSP上的實(shí)現(xiàn)與優(yōu)化方法,。首先，在算法上對霍夫圓變換使用MarrHildreth算子增強(qiáng)等方法進(jìn)行改進(jìn)以保證檢測的準(zhǔn)確率,；之后根據(jù) DSP的特點(diǎn),，利用C代碼優(yōu)化、浮點(diǎn)定點(diǎn)轉(zhuǎn)換和軟件流水等技術(shù)對算法進(jìn)行深度優(yōu)化,。實(shí)驗(yàn)結(jié)果表明,，程序的運(yùn)行時間明顯縮短，為視線檢測的實(shí)時性實(shí)現(xiàn)創(chuàng)造了良好的條件,。

關(guān)鍵詞：C6000 DSP,；霍夫變換；程序優(yōu)化

0引言

　　在視頻圖像中快速地檢測出圓形是目標(biāo)跟蹤,、目標(biāo)分類和行為理解等更高層次視頻圖像分析的重要基礎(chǔ),，比如人眼檢測、視線跟蹤和交通視頻分析等,?；舴驁A變換是圖像處理中識別和定位圓形的常用方法，其準(zhǔn)確率高且與圖中形狀的方向無關(guān)［12］,，被廣泛用于運(yùn)動目標(biāo)軌跡的檢測與識別,。在視線檢測領(lǐng)域，也有眾多關(guān)于它的研究,。MATHEWS R 提出了一種利用霍夫圓變換來設(shè)計(jì)鼠標(biāo)的方法［3］,，ZIA M A等人嘗試?yán)醚矍蜃粉檨頌闅埣踩嗽O(shè)計(jì)輪椅［4］。

　　標(biāo)準(zhǔn)霍夫變換雖然具有顯著的優(yōu)勢,，但其不足也不容忽視［56］,。它需消耗大量的時空資源，對于在嵌入式平臺上進(jìn)行視線檢測這樣的應(yīng)用背景無法做到實(shí)時控制,。目前有很多研究都僅針對算法上的改進(jìn),，而沒有結(jié)合具體的實(shí)現(xiàn)平臺的特點(diǎn)來進(jìn)行優(yōu)化，不能充分利用硬件的性能優(yōu)勢,。本文擬在德州儀器的TMS320C6000系列DSP上使用兩階段霍夫變換算法來實(shí)現(xiàn)圓形檢測,，并開展基于DSP平臺的程序優(yōu)化研究。

1改進(jìn)的兩階段霍夫圓變換算法

　　參考文獻(xiàn)［2］提出將霍夫變換一般化的方法，對于任何曲線,，只要給出了它的函數(shù)方程，就可以利用霍夫變換的方法,，將圖像空間變換到霍夫參數(shù)空間,，利用投票的方法求得曲線參數(shù)。對于檢測圓的情形,，由于圓的方程有3個未知量,，變換到霍夫空間中需要一個三維的累加器，對于高清圖片來說將耗費(fèi)大量的內(nèi)存,，而且搜索極值時時間代價很大,。這二者對于DSP平臺都是致命的，故在移植到DSP時本文采用了兩階段霍夫圓變換算法,，并對其進(jìn)行性能上的改進(jìn),。本節(jié)闡述了基于兩階段霍夫圓變換算法的圓檢測方案設(shè)計(jì)。

　　1.1兩階段霍夫圓變換算法

　　兩階段霍夫圓變換是一種針對標(biāo)準(zhǔn)霍夫圓變換的參數(shù)空間分解的方法,，主要目的是為了減少原算法的空間復(fù)雜度,，其輸入是邊緣圖像［5］。

　　考慮如下圓的參數(shù)方程：

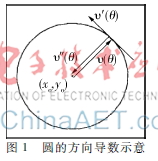
　　其中(x0,y0,r)是一組圓心和坐標(biāo)參數(shù),。兩階段霍夫圓變換的第一步是對圓心參數(shù)空間累加,。根據(jù)圓的一階導(dǎo)數(shù)和二階導(dǎo)數(shù)的特性，過圓周上任意一點(diǎn)的圓切線的垂線經(jīng)過圓心,，如圖1所示,。對已知邊緣上的任意點(diǎn)做垂線，這些垂線將會在(a, b)空間匯集,，形成一個熱點(diǎn),，在(a, b)空間搜索極值即得圓心坐標(biāo)。給定r的范圍,，在邊緣點(diǎn)上做垂線段,，得(a, b)空間。即：

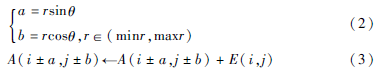
　　其中,，(minr,maxr)是給定的半徑的范圍,，也是做出的垂線段的長度，A是(a, b)空間的累加器,， E(i, j)是待檢測圖像的邊緣圖,。在(a, b)空間搜索極值即得圓心坐標(biāo)。

　　求得圓心坐標(biāo)之后,，在此基礎(chǔ)上可以進(jìn)行半徑參數(shù)空間的累加,。對每一個檢測的圓，R 空間累加方式為：

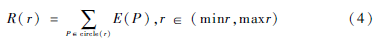
　　其中，E是邊緣圖,，r是給定的半徑范圍,。在R空間搜索極值即可求得半徑,。

　　1.2圓形檢測整體方案設(shè)計(jì)

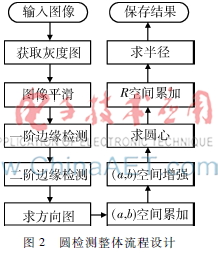
　　1.1節(jié)描述了一種節(jié)省空間開銷的霍夫變換方法，基于此,，本節(jié)設(shè)計(jì)了一套圓檢測方案，增加了預(yù)處理和利用MarrHildreth算子進(jìn)行圖像增強(qiáng)等步驟,，具體如圖2所示,。

　　由于形狀只與灰度值有關(guān),，故首先獲取灰度圖。之后,，對于含噪聲的圖像,，對其進(jìn)行平滑處理,，減少邊緣檢測的工作量和出錯率。平滑操作使用高斯平均算子,，模板大小為5,，方差為1,，實(shí)現(xiàn)時采用空域卷積的方式。為了保存更多的邊緣信息,，本文使用一階及二階邊緣檢測的方式來求取邊緣圖而不是直接對灰度圖進(jìn)行二值化。一階邊緣提取使用Sobel算子,，包括水平Sobel算子和垂直Sobel算子,，最后取二者的幾何平均作為最終的Sobel圖像。在使用圓的方向?qū)?shù)縮減參數(shù)空間時需要使用邊緣圖像的方向信息,，本文使用Sobel處理后的圖像來直接求得。

　　對于每個被檢測到的邊緣點(diǎn)(i,j),，計(jì)算其方向角度θ(i,j)：

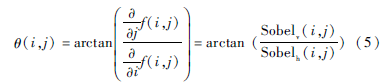
　　其中，f(i,j) 為邊緣圖像像素值,，Sobel(i,j)為Sobel處理后的像素值,，腳標(biāo)v,、h分別表示垂直和水平。C語言中atan2求得的角度值在 (-π, π) 間,，由于θ 與θ±π的方向相同,，可以將θ左右平移到區(qū)間 (-π2, π2)中,。

　　對于邊緣更復(fù)雜的圖像,，當(dāng)一階邊緣檢測過粗或者錯誤時，使用二階邊緣檢測能獲得更好的檢測效果,。MarrHildreth算子是利用高斯濾波的一種二階濾波方式,，它先對圖像進(jìn)行高斯平滑，之后應(yīng)用拉普拉斯運(yùn)算,，即：

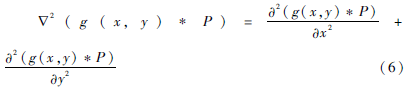
　　其中P是待處理的圖像,，g(x,y)是高斯平滑濾波器。此外,，MarrHildreth算子還被用于圖像增強(qiáng),。

　　在獲得邊緣圖像和邊緣方向信息之后使用1.1節(jié)中的方法就能求得圓心和半徑。

　　1.3圓形檢測中的實(shí)現(xiàn)細(xì)節(jié)

　　由于邊緣檢測的不精確性和待檢測圓的不確定性,，兩階段霍夫圓變換方法在實(shí)現(xiàn)的過程中存在一些問題,，本節(jié)將討論這些問題的解決方式。

　　使用式（2）,、（3）進(jìn)行(a,b)空間累加時,，會得到一些熱點(diǎn)，但是由于圓的形變等原因這些熱點(diǎn)常常是不清晰的或者彌漫開來的,，故有必要將它們聚集成一個更集中的點(diǎn),。使用式(6)MarrHildreth算子進(jìn)行圖像增強(qiáng)，將獲得更明亮的熱點(diǎn),。對增強(qiáng)后的(a, b)空間進(jìn)行閾值化處理,，得所求圓心。對于原圖中有多個圓的情形,，不同的閾值將保留不同數(shù)量的圓心,，數(shù)值越大,，對所檢測圓的要求越高，得到的圓心越少,。由于圓的大小不一,，得到的熱點(diǎn)（即圓心）亮度不一：大的圓在(a, b)空間中比小的圓累積值更大?？紤]在變換時添加衰減因子1k,，累加公式(3)可變?yōu)椋?/p>

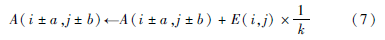
　　實(shí)驗(yàn)中發(fā)現(xiàn)大的圓由于邊緣方向估計(jì)誤差更大，在圓心區(qū)域的偏差會更大,，這會使它的聚集程度下降,，從而與由半徑大帶來的優(yōu)勢相抵消，此時k可設(shè)為1,。

　　在R空間使用式(4)時,，累加過程中只利用了垂線經(jīng)過圓心的邊緣點(diǎn)，由于誤差的原因?qū)е滦Ч惶?。考慮使用所有的邊緣點(diǎn)進(jìn)行累加,。設(shè)圓心與邊緣點(diǎn)的連線夾角是ψ,，則將垂線夾角在 (ψ-∈,ψ+∈) 間的邊緣點(diǎn)都加入計(jì)算，其中∈是允許誤差,，一般取π4或π8都能有較好的效果,。

　　對于同心圓，在R空間累加后選擇合適的閾值以保留多個峰值,，能獲得不同的半徑值,。

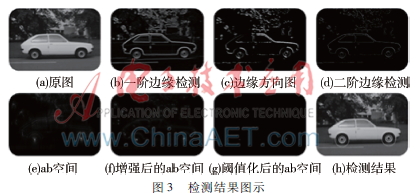
　　圖3是一組檢測結(jié)果示意圖。其中圖(c) 是將θ映射到(0,255) 得來,。在采取合適的參數(shù)后能獲得較好的檢測結(jié)果,。

2基于C6000 DSP的移植與優(yōu)化

　　2.1移植到DSP

　　本文使用的硬件平臺是TI的TMS320C64x+TM定點(diǎn)型DSP核，使用的開發(fā)環(huán)境為CCSv4,。使用C64x+ simulator進(jìn)行軟件仿真,，通過CCS的時鐘工具測得試運(yùn)行時鐘周期，通過profile工具分析工程耗時分布［7］,。

　　2.2具體的優(yōu)化步驟

　　本文的優(yōu)化基于所用DSP的結(jié)構(gòu)特性,，盡量充分利用DSP的計(jì)算資源來縮短檢測時間［89］。本節(jié)將介紹本文使用的優(yōu)化方法,。

　　2.2.1基于編譯器的優(yōu)化方法

　　CCS的編譯器中設(shè)置了眾多參數(shù),，選擇合適的參數(shù)能減少檢測耗時。

　　選擇優(yōu)化級別,。由于本文不考慮代碼體積,，故使用-o3文件級優(yōu)化,。

　　使用-mt。假設(shè)不存在多個指針對同一個內(nèi)存(塊)進(jìn)行讀寫操作,。

　　使用 -mh<num>,。 允許編譯器取超過數(shù)組邊界num字節(jié)的值。該操作使編譯器在編排軟件流水時有額外的彈性,，可提高流水性能,。在CMD文件中定義大于num的緩存空間，避免 EDMA或其他cache沖突,。

　　不使用 -g,、-ss等參數(shù)。這些參數(shù)對調(diào)試很有效,，但是會造成性能下降,，在最終發(fā)布產(chǎn)品時不應(yīng)使用。

　　CCS編譯器選項(xiàng)中有部分能減少手工整定時間但是對代碼性能沒有影響的參數(shù),，使用這些參數(shù)有助于程序優(yōu)化,。使用-s［-k|-al］-o［2|3］能生成優(yōu)化后的類似于C的代碼，且優(yōu)化器描述被嵌套在匯編代碼中,，使用-mw或者-mw-al輸出額外的關(guān)于軟件流水的信息,，包括單次循環(huán)的調(diào)度方式；使用-on2-o3生成*.nfo文件,，以給出高級別的優(yōu)化總結(jié)和可用的優(yōu)化建議,。

　　2.2.2手工整定方法

　　僅使用基于編譯器的優(yōu)化所減少的程序耗時是有限的，本文對算法的實(shí)時性要求較高,，需要在2.2.1節(jié)的基礎(chǔ)上進(jìn)行手工整定,。手工整定的方式很多，本文使用的幾種方法有基于編譯器和優(yōu)化器描述,、浮點(diǎn)定點(diǎn)轉(zhuǎn)換,、不用除法等。

　　根據(jù)優(yōu)化器描述給所有安全的指針添加restrict關(guān)鍵字,，消除循環(huán)間的依賴,，使生成的匯編文件中循環(huán)依賴項(xiàng)值為零；根據(jù)匯編嵌入信息添加pragma 指令MUST_ITERATE和UNROLL,，告訴編譯器循環(huán)的最大值,、最小值、公約數(shù)和展開次數(shù),，并根據(jù)軟件流水信息中各資源的使用情況在循環(huán)前使用 _nassert() 告訴編譯器數(shù)據(jù)是64位對齊的,，一次讀取多個對齊數(shù)據(jù)以減少D單元和T通道的使用數(shù)，以能較好地平衡資源,。這些措施極大地提高了軟件流水的效率,。

　　由于算法涉及眾多的浮點(diǎn)運(yùn)算,，在定點(diǎn)型甚至浮點(diǎn)型DSP中效率都很低，故在精度允許的情況下,，使用定點(diǎn)運(yùn)算代替浮點(diǎn)型運(yùn)算,。浮點(diǎn)轉(zhuǎn)換為定點(diǎn)除了手動使用Qn定標(biāo)外，對于C64x+ DSP還可以使用TI的C64x+ IQmath庫,。IQmath集合了很多高精度且高度優(yōu)化的數(shù)學(xué)函數(shù),，適合于將浮點(diǎn)的算法轉(zhuǎn)換成定點(diǎn)［10］。除了提供_iq數(shù)據(jù)類型及各類型互相轉(zhuǎn)換之外,，IQmath還提供了各種高度優(yōu)化的數(shù)學(xué)函數(shù)比如_IQcos(余弦函數(shù)),，并且支持可調(diào)節(jié)精度，在不同地方可以選擇不同的定標(biāo)Q值,，即GLOBAL_Q可以在需要的地方指定0~31中的任意值,。比如融合兩個Sobel算子時求兩個數(shù)的幾何平均：

　　(*imageTot)［i］［j］= pow( (*imageH)［i］［j］*(*imageH)［i］［j］ +(*imageV)［i］［j］*(*imageV)［i］［j］, 0.5f);

　　可以修改為：

　　tmp=_IQpow(*imageH［i］［j］,2) +_IQpow(*imageV［i］［j］,2);//sqrt(H^2+V^2)

　　*imageTot［i］［j］ = _IQsqrt(tmp);//pow(tmp,0.5f)

　　先將數(shù)據(jù)轉(zhuǎn)換成_iq類型，然后使用IQmath中的_IQpow和_IQsqrt來求冪和根號,，之后再轉(zhuǎn)換回需要的float型,。

　　對于除法運(yùn)算，DSP是利用函數(shù)調(diào)用來完成,，耗費(fèi)的時鐘周期比乘法高出2個數(shù)量級以上,。為了消除除法，可以使用移位或者查找表（lookup table）來代替,。比如:

　　(int)(_abs(im［i］［j］ + shift) /maxval*255);

　　其中maxval值在0~255之間，可以提前將255/maxval計(jì)算出來,，計(jì)算時查表代替,；或者使用8替代*255。另外,，使用 _IQdiv( _iq A, _iq B) 函數(shù)可完成_iq類型的除法,。

　　對于DSP的優(yōu)化方法還有很多，如使用內(nèi)聯(lián)函數(shù)和線性匯編等,，在進(jìn)一步優(yōu)化過程中可使用,。

　　2.3優(yōu)化結(jié)果與分析

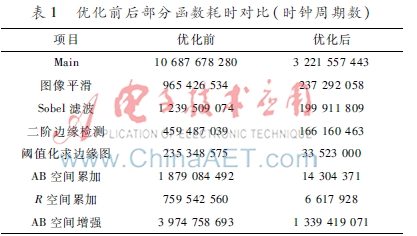
　　在綜合了各種優(yōu)化方式之后，重新使用profile測試各部分的時鐘周期,，保持其他條件不變,。程序優(yōu)化前后所用的時間見表1?？梢娊?jīng)過優(yōu)化,，耗時明顯減少。

3結(jié)論

　　本文先在PC上實(shí)現(xiàn)了基于霍夫變換的圓形檢測算法,，然后將它移植到了DSP上并進(jìn)行了基于時間的優(yōu)化分析,，使得實(shí)時性有很大的提高,。

　　若要將此算法應(yīng)用到人眼檢測，可以在前述的基礎(chǔ)上繼續(xù)改進(jìn),，比如縮減霍夫變換中r的范圍,，在R空間尋找峰值時指定目標(biāo)是2個等。本文所完成的只是視線跟蹤中人眼檢測的一部分,，離實(shí)際應(yīng)用還很遠(yuǎn),。本文設(shè)計(jì)還有很多不足，希望在未來的工作中繼續(xù)改進(jìn),。

參考文獻(xiàn)

　?。?］ BALLARD D H. Generalizing the Hough transform to detect arbitraryshapes［J］. Pattern Recognition, 1981, 13(2): 111122.

　　［2］ YUEN H K, PRINCEN J, ILLINGWORTH J. Comparative study of Hough transform methods for circle finding［J］. Image and Vision Computing, 1990, 8(1): 7177.

　?。?］ MATHEWS R, CHANDRA N. Computer mouse using eyetracking system based on houghman circle detection algorithm with grid analysis［J］. International Journal of Computer Applications, 2012, 40(13): 1216.

　?。?］ ZIA M A, ANSARI U, JAMIL M, et al.Face and eye detection in images using skin color segmentation and circular Hough transform［C］.Robotics and Emerging Allied Technologies in Engineering (iCREATE), 2014 International Conference on. IEEE, 2014: 211213.